Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-19T22:28:34.968Z Has data issue: false hasContentIssue false
  • English
  • Français

Transition scenario of a sphere freely falling in a vertical tube

Published online by Cambridge University Press:  20 September 2012

Thibaut Deloze ,
Yannick Hoarau  and
Jan Dušek
Thibaut Deloze*
Affiliation:
Institut de Mécanique des Fluides et des Solides, Université de Strasbourg/CNRS, 67000 Strasbourg, France
Yannick Hoarau
Affiliation:
Institut de Mécanique des Fluides et des Solides, Université de Strasbourg/CNRS, 67000 Strasbourg, France
Jan Dušek
Affiliation:
Institut de Mécanique des Fluides et des Solides, Université de Strasbourg/CNRS, 67000 Strasbourg, France
*
†Email address for correspondence: deloze@unistra.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper presents the results of direct numerical simulations of the fall of a single freely moving sphere in a vertical circular tube. Most results are obtained for the solid–fluid density ratio 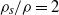. The parametric investigation is carried out depending on the Galileo number defined in Jenny, Dušek & Bouchet J. Fluid Mech., vol. 508, 2004, pp. 201–239. A qualitatively new scenario is found, as compared to that of an unconfined sphere. The primary bifurcation making the sphere deviate from a vertical fall along the tube axis at a constant velocity is of Hopf type. It sets in at a Galileo number (between 155 and 160) similar to that for an unconfined sphere. We find evidence for two stages of the primary regime: a planar trajectory at 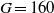and a helical one (at 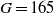and 170). At these Galileo numbers, the regime is perfectly periodic, with a slow period corresponding to a Strouhal number only slightly above 0.01. The dynamics is identified as a periodic wake–wall interaction. The helical regime is found to give way directly to chaos between 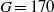and 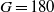. This transition is associated with the onset of vortex shedding in the wake of the falling sphere and with a complex interaction between the unsteady wake and the wall marked by intermittent wake extinction. The effect of density ratio is partly investigated at 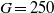by considering three density ratios: 2, 3 and 5. A significant change of behaviour is found between the ratios 3 and 5.

JFM classification

Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 711 , 25 November 2012 , pp. 40 - 60
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bagchi, P. & Balachandar, S. 2002 Effect of free rotation on the motion of a solid sphere in linear shear flow at moderate Re. Phys. Fluids 14, 2719.CrossRefGoogle Scholar
2. Borazjani, I., Ge, L. & Sotiropoulos, F. 2008 Curvilinear immersed boundary method for simulating fluid structure interaction with complex 3D rigid bodies. J. Comput. Phys. 227, 7587–7620.CrossRefGoogle ScholarPubMed
3. Chorin, A. J. 1968 Numerical solution of the Navier–Stokes equations. J. Math. Comput. 22, 745.CrossRefGoogle Scholar
4. Danaila, I., Dušek, J. & Anselmet, F. 1998 Nonlinear dynamics at a Hopf bifurcation with axisymmetry breaking in a jet. Phys. Rev. E 57, 3695–3698.Google Scholar
5. Deloze, T., Hoarau, Y. & Dušek, J. 2010 Chimera method applied to the simulation of a freely falling cylinder in a channel. Eur. J. Comput. Mech. 19, 575–590.CrossRefGoogle Scholar
6. Feng, J., Hu, H. H. & Joseph, D. D. 1994 Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid. Part 1. Sedimentation. J. Fluid Mech. 261, 95–134.CrossRefGoogle Scholar
7. Ghidersa, B. & Dušek, J. 2000 Breaking of axisymmetry and onset of unsteadiness in the wake of a sphere. J. Fluid Mech. 423, 33–69.CrossRefGoogle Scholar
8. Glowinski, R., Pan, T. W., Hesla, T. I., Joseph, D. D. & Periaux, J. 2001 A fictitious domain approach to the direct numerical simulation of incompressible viscous flow past moving rigid bodies: application to particulate flow. J. Comput. Phys. 169 (2), 363–426.CrossRefGoogle Scholar
9. Hu, H. H., Patankar, N. A. & Zhu, M. Y. 2001 Direct numerical simulations of fluid–solid systems using the arbitrary Lagrangian–Eulerian technique. J. Comput. Phys. 169 (2), 427–462.CrossRefGoogle Scholar
10. Jenny, M., Bouchet, G. & Dušek, J. 2003 Nonvertical ascension or fall of a free sphere in a Newtonian fluid. Phys. Fluids 15, L9.CrossRefGoogle Scholar
11. Jenny, M. & Dušek, J. 2004 Efficient numerical method for the direct numerical simulation of the flow past a single light moving spherical body in transitional regimes. J. Comput. Phys. 194, 215–232.CrossRefGoogle Scholar
12. Jenny, M., Dušek, J. & Bouchet, G. 2004 Instabilities and transition of a sphere falling or ascending freely in a Newtonian fluid. J. Fluid Mech. 508, 201–239.CrossRefGoogle Scholar
13. Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
14. Johnson, T. A. & Patel, V. C. 1999 Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 378, 19–70.CrossRefGoogle Scholar
15. Karnis, A., Goldsmith, H. L. & Mason, S. G. 1966 The flow of suspensions through tubes. Part 5. Inertial effects. Can. J. Chem. Engng 44 (4), 181–193.CrossRefGoogle Scholar
16. Kotouč, M., Bouchet, G. & Dušek, J. 2009 Transition to turbulence in the wake of a fixed sphere in mixed convection. J. Fluid Mech. 625, 205–248.CrossRefGoogle Scholar
17. Kurose, R. & Komori, S. 1999 Drag and lift forces on a rotating sphere in a linear shear flow. J. Fluid Mech. 384, 183–206.CrossRefGoogle Scholar
18. Matas, J. P., Morris, J. F. & Guazzelli, E. 2004 Inertial migration of rigid spherical particles in Poiseuille flow. J. Fluid Mech. 515, 171–195.Google Scholar
19. Namkoong, K., Yoo, J. Y. & Choi, H. G. 2008 Numerical analysis of two-dimensional motion of a freely falling circular cylinder in an infinite fluid. J. Fluid Mech. 604, 33–53.CrossRefGoogle Scholar
20. Ormières, D. & Provansal, M. 1999 Transition to turbulence in the wake of a sphere. Phys. Rev. Lett. 83, 80–83.CrossRefGoogle Scholar
21. Saffman, P. G. 1965 The lift on a small sphere in a slow shear flow. J. Fluid Mech. 22, 385–400.CrossRefGoogle Scholar
22. Segré, G. 1961 Radial particle displacements in Poiseuille flow of suspensions. Nature 189, 209–210.CrossRefGoogle Scholar
23. Segré, G. & Silberberg, A. 1962 Behaviour of macroscopic rigid spheres in Poiseuille flow. Part 1. Determination of local concentration by statistical analysis of particle passages through crossed light beams. J. fluid Mech. 14 (01), 115–135.Google Scholar
24. Takemura, F. & Magnaudet, J. 2003 The transverse force on clean and contaminated bubbles rising near a vertical wall at moderate Reynolds number. J. Fluid Mech. 495, 235–253.CrossRefGoogle Scholar
25. Takemura, F., Takagi, S., Magnaudet, J. & Matsumoto, Y. 2002 Drag and lift forces on a bubble rising near a vertical wall in a viscous liquid. J. Fluid Mech. 461, 277–300.CrossRefGoogle Scholar
26. Tomboulides, A. G. & Orszag, S. A. 2000 Numerical investigation of transitional and weak turbulent flow past a sphere. J. Fluid Mech. 416, 45–73.CrossRefGoogle Scholar
27. Uhlmann, M. 2005 An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 209, 448–476.CrossRefGoogle Scholar
28. Veldhuis, C. H. J. & Biesheuvel, A. 2007 An experimental study of the regimes of motion of spheres falling or ascending freely in a Newtonian fluid. Intl J. Multiphase Flow 33 (10), 1074–1087.CrossRefGoogle Scholar
29. Vos, J., Rizzi, A., Darracq, D. & Hirschel, E. 2002 Navier–Stokes solvers in European aircraft design. Prog. Aerosp. Sci. 38, 601–697.CrossRefGoogle Scholar
30. Yang, B. H., Wang, J., Joseph, D. D., Hu, H. H., Pan, T. W. & Glowinski, R. 2005 Migration of a sphere in tube flow. J. Fluid Mech. 540, 109–131.Google Scholar
31. Yu, Z., Phan-Thien, N., Fan, Y. & Tanner, R. I. 2002 Viscoelastic mobility problem of a system of particles. J. Non-Newtonian Fluid Mech. 104 (2–3), 87–124.CrossRefGoogle Scholar
32. Yu, Z., Phan-Thien, N. & Tanner, R. I. 2004 Dynamic simulation of sphere motion in a vertical tube. J. Fluid Mech. 518, 61–93.Google Scholar
33. Zeng, L., Balachandar, S. & Fischer, P. 2005 Wall-induced forces on a rigid sphere at finite Reynolds number. J. Fluid Mech. 536, 1–25.Google Scholar

Thibaut Deloze, Yannick Hoarau and Jan Dušek

Wake structures obtained using the λ2 iso-surfaces suggested by Jeong & Hussain (1995) behind a sphere free falling in a tube (D/d=5, G=250 and ρs/ρ=2). The thick red line marks the trajectory of the sphere centre.

Download Thibaut Deloze, Yannick Hoarau and Jan Dušek(Video)
Video 6.1 MB

Thibaut Deloze, Yannick Hoarau and Jan Dušek

Wake structures obtained using the λ2 iso-surfaces suggested by Jeong & Hussain (1995) behind a sphere free falling in a tube (D/d=5, G=250 and ρs/ρ=2). The thick red line marks the trajectory of the sphere centre.

Download Thibaut Deloze, Yannick Hoarau and Jan Dušek(Video)
Video 6.8 MB