Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-17T14:38:51.615Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional instabilities of quasi-solitary waves in a falling liquid film

Published online by Cambridge University Press:  29 September 2014

N. Kofman ,
S. Mergui  and
C. Ruyer-Quil
N. Kofman
Affiliation:
UPMC Université Paris 06, Université Paris-Sud, CNRS, laboratoire FAST, bâtiment 502, Campus universitaire, Orsay F-91405, France
S. Mergui*
Affiliation:
UPMC Université Paris 06, Université Paris-Sud, CNRS, laboratoire FAST, bâtiment 502, Campus universitaire, Orsay F-91405, France
C. Ruyer-Quil
Affiliation:
Université de Savoie, CNRS, laboratoire LOCIE, Savoie Technolac, Le Bourget du Lac 73376 CEDEX, France Institut Universitaire de France (IUF), France
*
†Email address for correspondence: mergui@fast.u-psud.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

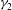The stability of $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\gamma _2$ travelling waves at the surface of a film flow down an inclined plane is considered experimentally and numerically. These waves are fast, one-humped and quasi-solitary. They undergo a three-dimensional secondary instability if the flow rate (or Reynolds number) is sufficiently high. Rugged or scallop wave patterns are generated by the interplay between a short-wave and a long-wave instability mode. The short-wave mode arises in the capillary region of the wave, with a mechanism of capillary origin which is similar to the Rayleigh–Plateau instability, whereas the long-wave mode deforms the entire wave and is triggered by a Rayleigh–Taylor instability. Rugged waves are observed at relatively small inclination angles. At larger angles, the long-wave mode predominates and scallop waves are observed. For a water film the transition between rugged and scallop waves occurs for an inclination angle around 12°.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Waves/Free-surface Flows: Solitary waves Interfacial Flows (free surface): Thin films
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 854 - 887
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alekseenko, S. V., Nakoryakov, V. Y. & Pokusaev, B. G. 1985 Wave formation on a vertical falling liquid film. AIChE J. 31, 1446–1460.CrossRefGoogle Scholar
Alekseenko, S. V., Nakoryakov, V. E. & Pokusaev, B. G. 1994 Wave Flow in Liquid Films, 3rd edn. Begell House.CrossRefGoogle Scholar
Allen, R. F. 1975 The role of surface tension in splashing. J. Colloid Interface Sci. 51 (2), 350–351.CrossRefGoogle Scholar
Bakopoulos, A. 1980 Liquid-side controlled mass transfer in wetted-wall tubes. Ger. Chem. Engng 3, 241–252.Google Scholar
Balmforth, N. J. & Liu, J. J. 2004 Roll waves in mud. J. Fluid Mech. 519, 33–54.CrossRefGoogle Scholar
Benjamin, T. B. 1957 Wave formation in laminar flow down an inclined plane. J. Fluid Mech. 2, 554–574.CrossRefGoogle Scholar
Bo, S., Ma, X., Lan, Z., Chen, J. & Chen, H. 2010 Numerical simulation on the falling film absorption process in a counter-flow absorber. Chem. Engng J. 156, 607–612.CrossRefGoogle Scholar
Chang, H. C., Demekhin, E. A. & Kopelevitch, D. I. 1993 Nonlinear evolution of waves on a vertically falling film. J. Fluid Mech. 250, 433–480.CrossRefGoogle Scholar
Cheng, M. & Chang, H. C. 1995 Competition between subharmonic and sideband secondary instabilities on a falling film. Phys. Fluids 7 (1), 34–54.CrossRefGoogle Scholar
Demekhin, E. A. & Kalaidin, E. N. 2007 Three-dimensional localized coherent structures of surface turbulence. I. Scenarios of two-dimensional-three-dimensional transition. Phys. Fluids 19, 114103.Google Scholar
Demekhin, E. A., Kalaidin, E. N., Kalliadasis, S. & Vlaskin, S. Y. 2007 Three-dimensional localized coherent structures of surface turbulence. II. $\lambda $ solitons. Phys. Fluids 19, 114104.Google Scholar
Demekhin, E. A., Kalaidin, E. N. & Selin, A. S. 2010 Three-dimensional localized coherent structures of surface turbulence. III. Experiment and model validation. Phys. Fluids 22, 092103.CrossRefGoogle Scholar
Dietze, G. F., Al-Sibai, F. & Kneer, R. 2009 Experimental study of flow separation in laminar falling liquid films. J. Fluid Mech. 637, 73–104.CrossRefGoogle Scholar
Dietze, G. F., Leefken, A. & Kneer, R. 2008 Investigation of the backflow phenomenon in falling liquid films. J. Fluid Mech. 595, 435–459.CrossRefGoogle Scholar
Doedel, E. J. 2008 Auto07p continuation and bifurcation software for ordinary differential equations. Montreal Concordia University.Google Scholar
Frisk, D. P. & Davis, E. J. 1972 The enhancement of heat transfer by waves in stratified gas–liquid flow. Intl J. Heat Mass Transfer 15, 1537–1552.CrossRefGoogle Scholar
Fujita, T. 1993 Falling liquid films in absorption machines. Intl J. Refrig. 16, 282–294.CrossRefGoogle Scholar
Germain, P. 1973 Cours de Mécanique des Milieux Continus. Masson.Google Scholar
Heining, C., Pollak, T. & Aksel, N. 2012 Pattern formation and mixing in three-dimensional film flow. Phys. Fluids 24, 042102.CrossRefGoogle Scholar
Kalliadasis, S., Ruyer-Quil, C., Scheid, B. & Velarde, M. G. 2012 Falling Liquid Films. Springer.CrossRefGoogle Scholar
Krechetnikov, R. 2009 Rayleigh–Taylor and Richtmeyer–Meshkov instabilities of flat and curved interfaces. J. Fluid Mech. 625, 387–410.CrossRefGoogle Scholar
Leontidis, V., Vatteville, J., Vlachogiannis, M., Andritsos, N. & Bontozoglou, V. 2010 Nominally two-dimensional waves in inclined film flow in channels of finite width. Phys. Fluids 22, 112106.CrossRefGoogle Scholar
Liu, J. & Gollub, J. P. 1994 Solitary wave dynamics of film flows. Phys. Fluids 6, 1702–1712.CrossRefGoogle Scholar
Liu, J., Schneider, J. B. & Gollub, J. P. 1995 Three-dimensional instabilities of film flows. Phys. Fluids 7 (1), 55–67.CrossRefGoogle Scholar
Marmottant, P. & Villermaux, E. 2004 On spray formation. J. Fluid Mech. 498, 73–111.CrossRefGoogle Scholar
Moisy, F., Rabaud, M. & Salsac, K. 2009 A synthetic schlieren method for the measurement of the topography of a liquid interface. Exp. Fluids 46 (6), 1021–1036.CrossRefGoogle Scholar
Oron, A., Gottlieb, O. & Novbari, E. 2007 Bifurcations of a weighted-residual integral boundary-layer model for nonlinear dynamics of falling liquid films. J. Phys.: Conf. Ser. 64 (1), 012007.Google Scholar
Park, C. D. & Nosoko, T. 2003 Three-dimensional wave dynamics on a falling film and associated mass transfer. AIChE J. 49 (11), 2715–2727.CrossRefGoogle Scholar
Rastaturin, A., Demekhin, E. & Kalaidin, E. 2006 Optimal regimes of heat-mass transfer in falling film. J. Non-Equilib. Thermodyn. 31, 1–10.CrossRefGoogle Scholar
Rayleigh, L. 1883 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. 14, 170–177.Google Scholar
Ribe, N. M. 2001 Bending and stretching of thin viscous sheets. J. Fluid Mech. 433, 135–160.CrossRefGoogle Scholar
Ruyer-Quil, C.1999 Dynamique d’un film mince s’écoulant le long d’un plan incliné. PhD thesis, École Polytechnique, LadHyx, France.Google Scholar
Ruyer-Quil, C. & Manneville, P. 2000 Improved modeling of flows down inclined planes. Eur. Phys. J. B 15, 357–369.CrossRefGoogle Scholar
Scheid, B., Kalliadasis, S., Ruyer-Quil, C. & Colinet, P. 2008 Interaction of three-dimensional hydrodynamic and thermocapillary instabilities in film flows. Phys. Rev. E 78, 066311.CrossRefGoogle ScholarPubMed
Scheid, B., Ruyer-Quil, C. & Manneville, P. 2006 Wave patterns in film flows: modelling and three-dimensional waves. J. Fluid Mech. 562, 183–222.CrossRefGoogle Scholar
Scheid, B., Ruyer-Quil, C., Thiele, U., Kabov, O. A., Legros, J. C. & Colinet, P. 2005 Validity domain of the Benney equation including the Marangoni effect for closed and open flows. J. Fluid Mech. 527, 303–335.CrossRefGoogle Scholar
Schlichting, H., Gersten, K. & Krause, E. 2004 Boundary-Layer Theory, 8th edn Springer.Google Scholar
Shkadov, V. Ya. 1967 Wave flow regimes of a thin layer of viscous fluid subject to gravity. Izv. Akad. Nauk, SSSR Mekh. Zhidk. Gaza 1, 43–51; English translation in Fluid Dyn. 2, 29–34, 1970 (Faraday Press, NY).Google Scholar
Shkadov, V. Ya. 1977 Solitary waves in a layer of viscous liquid. Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza 1, 63–66.Google Scholar
Shkadov, V. Ya. & Sisoev, G. M. 2004 Waves induced by instability in falling films of finite thickness. Fluid Dyn. Res. 35, 357–389.CrossRefGoogle Scholar
Skotheim, J. M., Thiele, U. & Scheid, B. 2003 On the instability of a falling film due to localized heating. J. Fluid Mech. 475, 1–19.CrossRefGoogle Scholar
Spaid, N. & Homsy, G. 1996 Stability of Newtonian and viscoelastic dynamic contact lines. Phys. Fluids 8, 460–478.CrossRefGoogle Scholar
Taylor, G. I. 1950 The instability of liquid surfaces whan accelerated in a direction perpendicular to their planes. Part 1. Waves on fluid sheets. Proc. R. Soc. Lond. 201, 192–196.Google Scholar
Vlachogiannis, M., Samandas, A., Leontidis, V. & Bontozoglou, V. 2010 Effect of channel width on the primary instability of inclined film flow. Phys. Fluids 22, 012106.CrossRefGoogle Scholar
Yoshimura, P. N., Nosoko, T. & Nagata, T. 1996 Enhancement of mass transfer by waves into a falling laminar liquid film by two-dimensional surface waves – some experimental observations and modeling. Chem. Engng Sci. 51, 1231–1240.CrossRefGoogle Scholar