Hostname: page-component-77c89778f8-gq7q9 Total loading time: 0 Render date: 2024-07-20T19:33:43.574Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional doubly diffusive convectons: instability and transition to complex dynamics

Published online by Cambridge University Press:  06 February 2018

Cédric Beaume Open the ORCID record for Cédric Beaume [Opens in a new window] ,
Alain Bergeon  and
Edgar Knobloch
Cédric Beaume*
Affiliation:
School of Mathematics, University of Leeds, Leeds LS2 9JT, UK
Alain Bergeon
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, CNRS, 31400 Toulouse, France
Edgar Knobloch
Affiliation:
Department of Physics, University of California, Berkeley, CA 94720, USA
*
†Email address for correspondence: c.m.l.beaume@leeds.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Three-dimensional doubly diffusive convection in a closed vertically extended container driven by competing horizontal temperature and concentration gradients is studied by a combination of direct numerical simulation and linear stability analysis. No-slip boundary conditions are imposed on all six container walls. The buoyancy number 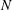$N$ is taken to be 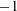$-1$ to ensure the presence of a conduction state. The primary instability is subcritical and generates two families of spatially localized steady states known as convectons. The convectons bifurcate directly from the conduction state and are organized in a pair of primary branches that snake within a well-defined range of Rayleigh numbers as the convectons grow in length. Secondary instabilities generating twist result in secondary snaking branches of twisted convectons. These destabilize the primary convectons and are responsible for the absence of stable steady states, localized or otherwise, in the subcritical regime. Thus all initial conditions in this regime collapse to the conduction state. As a result, once the Rayleigh number for the primary instability of the conduction state is exceeded, the system exhibits an abrupt transition to large-amplitude relaxation oscillations resembling bursts with no hysteresis. These numerical results are confirmed here by determining the stability properties of both convecton types as well as the domain-filling states. The number of unstable modes of both primary and secondary convectons of different lengths follows a pattern that allows the prediction of their stability properties based on their length alone. The instability of the convectons also results in a dramatic change in the dynamics of the system outside the snaking region that arises when the twist instability operates on a time scale faster than the time scale on which new rolls are nucleated. The results obtained are expected to be applicable in various pattern-forming systems exhibiting localized structures, including convection and shear flows.

JFM classification

Convection: Double diffusive convection Instability: Instability Nonlinear Dynamical Systems: Nonlinear Dynamical Systems
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 840 , 10 April 2018 , pp. 74 - 105
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, M., Mellibovsky, F., Roland, N. & Hof, B. 2013 Streamwise-localized solutions at the onset of turbulence in pipe flow. Phys. Rev. Lett. 110, 224502.Google Scholar
Avitabile, D., Lloyd, D. J. B., Burke, J., Knobloch, E. & Sandstede, B. 2010 To snake or not to snake in the planar Swift–Hohenberg equation. SIAM J. Appl. Dyn. Syst. 9, 704–733.Google Scholar
Batiste, O., Knobloch, E., Alonso, A. & Mercader, I. 2006 Spatially localized binary-fluid convection. J. Fluid Mech. 560, 149–158.Google Scholar
Beaume, C. 2017 Adaptive Stokes preconditioning for steady incompressible flows. Commun. Comput. Phys. 22, 494–516.Google Scholar
Beaume, C., Bergeon, A. & Knobloch, E. 2011 Homoclinic snaking of localized states in doubly diffusive convection. Phys. Fluids 23, 094102.Google Scholar
Beaume, C., Bergeon, A. & Knobloch, E. 2013a Convectons and secondary snaking in three-dimensional natural doubly diffusive convection. Phys. Fluids 25, 024105.Google Scholar
Beaume, C., Knobloch, E. & Bergeon, A. 2013b Nonsnaking doubly diffusive convectons and the twist instability. Phys. Fluids 25, 114102.Google Scholar
Bergeon, A. & Knobloch, E. 2002 Natural doubly diffusive convection in three-dimensional enclosures. Phys. Fluids 14, 3233–3250.Google Scholar
Bergeon, A. & Knobloch, E. 2008a Periodic and localized states in natural doubly diffusive convection. Physica D 237, 1139–1150.Google Scholar
Bergeon, A. & Knobloch, E. 2008b Spatially localized states in natural doubly diffusive convection. Phys. Fluids 20, 034102.Google Scholar
Brand, E. & Gibson, J. F. 2014 A doubly localized equilibrium solution of plane Couette flow. J. Fluid Mech. 750, R3.Google Scholar
Burke, J. & Dawes, J. H. P. 2012 Localized states in an extended Swift–Hohenberg equation. SIAM J. Appl. Dyn. Syst. 11, 261–284.Google Scholar
Burke, J. & Knobloch, E. 2006 Localized states in the generalized Swift–Hohenberg equation. Phys. Rev. E 73, 056211.Google Scholar
Burke, J. & Knobloch, E. 2007a Homoclinic snaking: structure and stability. Chaos 17, 037102.Google Scholar
Burke, J. & Knobloch, E. 2007b Snakes and ladders: localized states in the Swift–Hohenberg equation. Phys. Lett. A 360, 681–688.Google Scholar
Dangelmayr, G., Hettel, J. & Knobloch, E. 1997 Parity-breaking bifurcation in inhomogeneous systems. Nonlinearity 74, 1093–1114.Google Scholar
Duguet, Y., Schlatter, P. & Henningson, D. 2009 Localized edge states in plane Couette flow. Phys. Fluids 21, 111701.Google Scholar
Ghorayeb, K. & Mojtabi, A. 1997 Double diffusive convection in a vertical regular cavity. Phys. Fluids 9, 2339–2348.Google Scholar
Gibson, J. F. & Brand, E. 2014 Spanwise-localized solutions of planar shear flows. J. Fluid Mech. 745, 25–61.Google Scholar
Gibson, J. F. & Schneider, T. M. 2016 Homoclinic snaking in plane Couette flows: bending, skewing and finite-size effects. J. Fluid Mech. 794, 530–551.Google Scholar
Hirschberg, P. & Knobloch, E. 1997 Mode interactions in large aspect ratio convection. J. Nonlinear Sci. 7, 537–556.Google Scholar
Kao, H.-C., Beaume, C. & Knobloch, E. 2014 Spatial localization in heterogeneous systems. Phys. Rev. E 89, 012903.Google Scholar
Khapko, T., Kreilos, T., Schlatter, P., Duguet, Y., Eckhardt, B. & Henningson, D. 2013 Localized edge states in the asymptotic suction boundary layer. J. Fluid Mech. 717, R6.CrossRefGoogle Scholar
Knobloch, E. 2015 Spatial localization in dissipative systems. Annu. Rev. Cond. Mat. Phys. 6, 325–359.Google Scholar
Knobloch, E., Hettel, J. & Dangelmayr, G. 1995 Parity breaking bifurcation in inhomogeneous systems. Phys. Rev. Lett. 74, 4839–4842.Google Scholar
Lioubashevski, O., Hamiel, Y., Agnon, A., Reches, Z. & Fineberg, J. 1999 Oscillons and propagating solitary waves in a vertically vibrated colloidal suspension. Phys. Rev. Lett. 83, 3190–3193.Google Scholar
Lloyd, D. J. B., Gollwitzer, C., Rehberg, I. & Richter, R. 2015 Homoclinic snaking near the surface instability of a polarizable fluid. J. Fluid Mech. 783, 283–305.Google Scholar
Lo Jacono, D., Bergeon, A. & Knobloch, E. 2017 Localized traveling pulses in natural doubly diffusive convection. Phys. Rev. Fluids 2, 093501.Google Scholar
Mellibovsky, F. & Meseguer, A. 2015 A mechanism for streamwise localisation of nonlinear waves in shear flows. J. Fluid Mech. 779, R1.Google Scholar
Mercader, I., Alonso, A. & Batiste, O. 2008 Spatiotemporal dynamics near the onset of convection for binary mixtures in cylindrical containers. Phys. Rev. E 77, 036313.Google Scholar
Mercader, I., Batiste, O., Alonso, A. & Knobloch, E. 2009 Localized pinning states in closed containers: Homoclinic snaking without bistability. Phys. Rev. E 80, 025201(R).Google Scholar
Mercader, I., Batiste, O., Alonso, A. & Knobloch, E. 2011 Convectons, anticonvectons and multiconvectons in binary fluid convection. J. Fluid Mech. 667, 586–606.Google Scholar
Mercader, I., Batiste, O., Alonso, A. & Knobloch, E. 2013 Travelling convectons in binary fluid convection. J. Fluid Mech. 722, 240–266.Google Scholar
Merkin, J. H., Petrov, V., Scott, S. K. & Showalter, K. 1996a Wave-induced chaos in a continuously fed unstirred reactor. J. Chem. Soc. Faraday Trans. 92, 2911–2918.Google Scholar
Merkin, J. H., Petrov, V., Scott, S. K. & Showalter, K. 1996b Wave-induced chemical chaos. Phys. Rev. Lett. 76, 546–549.Google Scholar
Nishiura, Y. & Ueyama, D. 2001 Spatio-temporal chaos for the Gray–Scott model. Physica D 150, 137–162.Google Scholar
Schneider, T. M., Gibson, J. F. & Burke, J. 2010a Snakes and ladders: localized solutions of plane Couette flow. Phys. Rev. Lett. 104, 104501.Google Scholar
Schneider, T. M., Marinc, D. & Eckhardt, B. 2010b Localized edge states nucleate turbulence in extended plane Couette cells. J. Fluid Mech. 646, 441–451.Google Scholar
Sezai, I. & Mohamad, A. A. 2000 Double diffusive convection in a cubic enclosure with opposing temperature and concentration gradients. Phys. Fluids 12, 2210–2223.Google Scholar
Thangam, S., Zebib, A. & Chen, C. F. 1982 Double-diffusive convection in an inclined fluid layer. J. Fluid Mech. 116, 363–378.Google Scholar
Watanabe, T., Iima, M. & Nishiura, Y. 2012 Spontaneous formation of travelling localized structures and their asymptotic behaviour in binary fluid convection. J. Fluid Mech. 712, 219–243.Google Scholar
Watanabe, T., Iima, M. & Nishiura, Y. 2016 A skeleton of collision dynamics: Hierarchical network structure among even-symmetric steady pulses in binary fluid convection. SIAM J. Appl. Dyn. Syst. 15, 789–806.Google Scholar
Woods, P. D. & Champneys, A. R. 1999 Heteroclinic tangles and homoclinic snaking in the unfolding of a degenerate reversible Hamiltonian–Hopf bifurcation. Physica D 129, 147–170.Google Scholar
Xin, S., Le Quéré, P. & Tuckerman, L. S. 1998 Bifurcation analysis of double-diffusive convection with opposing horizontal thermal and solutal gradients. Phys. Fluids 10, 850–858.Google Scholar