Article contents
Temperature dynamics in decaying isotropic turbulence with Joule heat production
Published online by Cambridge University Press: 29 April 2013
Abstract
This paper presents an extension of existing works dealing with the dynamics of a passive scalar in freely decaying isotropic turbulence, by accounting for a production mechanism of the passive scalar itself. The physically relevant case of the temperature dynamics in the presence of Joule heating via the dissipation of the turbulent kinetic energy is selected and analysed by theoretical and numerical means. In particular, the sensitivity of the temperature decay to the non-dimensional parameters Prandtl number (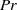 $\mathit{Pr}$) and Eckert number (
$\mathit{Pr}$) and Eckert number (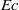 $\mathit{Ec}$), the latter measuring the intensity of the internal energy production mechanism, is investigated. The time behaviour of the global quantities such as the temperature variance
$\mathit{Ec}$), the latter measuring the intensity of the internal energy production mechanism, is investigated. The time behaviour of the global quantities such as the temperature variance 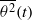 $ \overline{{\theta }^{2} } (t)$ and its destruction rate
$ \overline{{\theta }^{2} } (t)$ and its destruction rate 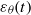 ${\varepsilon }_{\theta } (t)$ is analysed, and a detailed analysis of the temperature variance spectrum
${\varepsilon }_{\theta } (t)$ is analysed, and a detailed analysis of the temperature variance spectrum 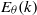 ${E}_{\theta } (k)$ is provided. In the case of a very strong heating mechanism, some important modifications of the temperature dynamics are observed. The time-decay-law exponents of the global physical quantities assume new values, which are governed only by features of the kinetic energy spectrum, while they depend on the shape of
${E}_{\theta } (k)$ is provided. In the case of a very strong heating mechanism, some important modifications of the temperature dynamics are observed. The time-decay-law exponents of the global physical quantities assume new values, which are governed only by features of the kinetic energy spectrum, while they depend on the shape of 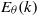 ${E}_{\theta } (k)$ in the classical free-decay case. The temperature variance spectrum
${E}_{\theta } (k)$ in the classical free-decay case. The temperature variance spectrum 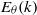 ${E}_{\theta } (k)$ exhibits two new spectral ranges. One is a convective–production range such that
${E}_{\theta } (k)$ exhibits two new spectral ranges. One is a convective–production range such that 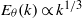 ${E}_{\theta } (k)\propto {k}^{1/ 3} $ is observed for a finite time at all values of
${E}_{\theta } (k)\propto {k}^{1/ 3} $ is observed for a finite time at all values of 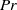 $\mathit{Pr}$. In the case of very diffusive fluids with
$\mathit{Pr}$. In the case of very diffusive fluids with 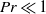 $\mathit{Pr}\ll 1$, a convective–diffusive–production range with
$\mathit{Pr}\ll 1$, a convective–diffusive–production range with 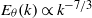 ${E}_{\theta } (k)\propto {k}^{- 7/ 3} $ is also detected.
${E}_{\theta } (k)\propto {k}^{- 7/ 3} $ is also detected.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 11
- Cited by


