Article contents
A systematic investigation of roughness height and wavelength in turbulent pipe flow in the transitionally rough regime
Published online by Cambridge University Press: 27 April 2015
Abstract
Direct numerical simulations (DNS) are conducted for turbulent flow through pipes with three-dimensional sinusoidal roughnesses explicitly represented by body-conforming grids. The same viscous-scaled roughness geometry is first simulated at a range of different Reynolds numbers to investigate the effects of low Reynolds numbers and low 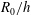 $R_{0}/h$, where
$R_{0}/h$, where 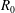 $R_{0}$ is the pipe radius and
$R_{0}$ is the pipe radius and 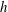 $h$ is the roughness height. Results for the present class of surfaces show that the Hama roughness function
$h$ is the roughness height. Results for the present class of surfaces show that the Hama roughness function 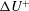 ${\rm\Delta}U^{+}$ is only marginally affected by low Reynolds numbers (or low
${\rm\Delta}U^{+}$ is only marginally affected by low Reynolds numbers (or low 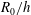 $R_{0}/h$), and observations of outer-layer similarity (or lack thereof) show no signs of sensitivity to Reynolds number. Then, building on this, a systematic approach is taken to isolate the effects of roughness height
$R_{0}/h$), and observations of outer-layer similarity (or lack thereof) show no signs of sensitivity to Reynolds number. Then, building on this, a systematic approach is taken to isolate the effects of roughness height 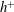 $h^{+}$ and wavelength
$h^{+}$ and wavelength 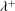 ${\it\lambda}^{+}$ in a turbulent wall-bounded flow in both transitionally rough and fully rough regimes. Current findings show that while the effective slope
${\it\lambda}^{+}$ in a turbulent wall-bounded flow in both transitionally rough and fully rough regimes. Current findings show that while the effective slope 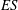 $\mathit{ES}$ (which for the present sinusoidal surfaces is proportional to
$\mathit{ES}$ (which for the present sinusoidal surfaces is proportional to 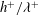 $h^{+}/{\it\lambda}^{+}$) is an important roughness parameter, the roughness function
$h^{+}/{\it\lambda}^{+}$) is an important roughness parameter, the roughness function 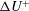 ${\rm\Delta}U^{+}$ must also depend on some measure of the viscous roughness height. A simplistic linear–log fit clearly illustrates the strong correlation between
${\rm\Delta}U^{+}$ must also depend on some measure of the viscous roughness height. A simplistic linear–log fit clearly illustrates the strong correlation between 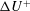 ${\rm\Delta}U^{+}$ and both the roughness average height
${\rm\Delta}U^{+}$ and both the roughness average height 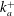 $k_{a}^{+}$ (which is related to
$k_{a}^{+}$ (which is related to 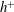 $h^{+}$) and
$h^{+}$) and 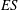 $\mathit{ES}$ for the surfaces simulated here, consistent with published literature. Various definitions of the virtual origin for rough-wall turbulent pipe flow are investigated and, for the surfaces simulated here, the hydraulic radius of the pipe appears to be the most suitable parameter, and indeed is the only virtual origin that can ever lead to collapse in the total stress. First- and second-order statistics are also analysed and collapses in the outer layer are observed for all cases, including those where the largest roughness height is a substantial proportion of the reference radius (low
$\mathit{ES}$ for the surfaces simulated here, consistent with published literature. Various definitions of the virtual origin for rough-wall turbulent pipe flow are investigated and, for the surfaces simulated here, the hydraulic radius of the pipe appears to be the most suitable parameter, and indeed is the only virtual origin that can ever lead to collapse in the total stress. First- and second-order statistics are also analysed and collapses in the outer layer are observed for all cases, including those where the largest roughness height is a substantial proportion of the reference radius (low 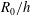 $R_{0}/h$). These results provide evidence that turbulent pipe flow over the present sinusoidal surfaces adheres to Townsend’s notion of outer-layer similarity, which pertains to statistics of relative motion.
$R_{0}/h$). These results provide evidence that turbulent pipe flow over the present sinusoidal surfaces adheres to Townsend’s notion of outer-layer similarity, which pertains to statistics of relative motion.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 137
- Cited by





