1 Introduction
Swimming micro-organisms are ubiquitous, including oceanic micro-algae and human gut bacteria. To clarify swimming dynamics, several fluid mechanical models have been created to deal with the various geometries and swimming modes of natural micro-organisms. Lighthill (Reference Lighthill1952) introduced a simplified ciliate model, the so-called ‘squirmer’. The model was generalised by Blake (Reference Blake1971) and has been used to analyse various ciliate species. Brennen (Reference Brennen1974) outlined a fluid mechanical model of self-propelled micro-organisms by introducing an oscillating boundary layer theory for ciliary propulsion. Keller & Wu (Reference Keller and Wu1977) built on the model by extending the squirmer to be prolate spheroidal in shape, and estimated the effect of shape on energy expenditure. Michelin & Lauga (Reference Michelin and Lauga2010) showed that the minimum energy dissipation at a given swimming speed was afforded by a neutral swimmer, thus neither a puller nor a pusher. Magar, Goto & Pedley (Reference Magar, Goto and Pedley2003) investigated microbial nutrient uptake from the environment. Squirming enhanced uptake compared to that of a rigid sphere moving at the same speed. Ishikawa et al. (Reference Ishikawa, Kajiki, Imai and Omori2016) extended the analysis to squirmer suspensions; nutrient uptake increased in a quadratic manner to volume fractions of up to 30 %. The squirmer model has also been used to study bioconvection in suspensions of upswimming cells, which generate gravitational instability (Kessler Reference Kessler1986; Ishikawa, Locsei & Pedley Reference Ishikawa, Locsei and Pedley2008; Evans et al. Reference Evans, Ishikawa, Yamaguchi and Lauga2011), and to explore the coherent structures of non-gravitational active swimmers (Simha & Ramaswamy Reference Simha and Ramaswamy2002; Saintillan & Shelley Reference Saintillan and Shelley2008). Ishikawa & Pedley (Reference Ishikawa and Pedley2007) computed the translational diffusion tensors of squirmers in semi-dilute suspensions; these can also be derived analytically at the dilution limits. Pedley, Brumley & Goldstein (Reference Pedley, Brumley and Goldstein2016) extended the Lighthill–Blake squirmer to incorporate an azimuthal swirl mode. The details can be found in a recent review by Pedley (Reference Pedley2016).
The Lighthill–Blake squirmer is a sphere with a deformable surface reflecting periodic ciliary beating. The squirming surface is defined by the mean height of ciliary tips that exhibit low-amplitude oscillations. The deformable/stretchable spherical surface is considered to be an envelope marking the boundary of beating ciliary tips. When squirming velocity on the deformable surface is considered in both the radial and tangential directions, the body swims with a non-zero mean velocity. The squirmer model describes fluid motions outside the ciliary envelope; flow inside the envelope is ignored. In reality, however, fluid flow exists even within the envelope. Only a few studies (e.g. Keller & Wu Reference Keller and Wu1977) have compared the energy expenditure within the ciliary layer to that outside the ciliary layer. Thus, flow generated by individual ciliary motions inside the envelope requires further attention.
Cilia-driven flow has been investigated by several groups (Blake Reference Blake1972, Reference Blake1974; Niedermayer, Eckhardt & Lenz Reference Niedermayer, Eckhardt and Lenz2008; Brumley et al. Reference Brumley, Polin, Pedley and Goldstein2012; Eloy & Lauga Reference Eloy and Lauga2012; Elgeti & Gompper Reference Elgeti and Gompper2013; Nasouri & Elfring Reference Nasouri and Elfring2016). In cilia-driven flows, metachronal wave propagation plays a role, and four metachronal wave patterns have been recognised (Sleigh Reference Sleigh1962): a symplectic metachronal wave (the beat direction and that of wave transmission coincide); an antiplectic metachronal wave (the two directions are opposed); a dexioplectic metachronal wave (the effective beat moves to the right with respect to the direction of wave transmission); and a laeoplectic metachronal wave (the effective beat moves to the left with respect to the direction of wave transmission). These different wave patterns have been observed in various species. For example, symplectic waves are characteristic of Opalina (Sleigh Reference Sleigh1962) and dexioplectic wave propagation has been observed in Paramecium swimming under normal conditions (Machemer Reference Machemer1972). Blake (Reference Blake1972) analysed the force, bending moment and rate of work exerted on a cilium with various types of metachronism. He reported that in antiplectic metachronism neighbouring cilia spread out during the effective stroke. Thus, the force exerted on a cilium and the rate of work were large during the effective stroke. Eloy & Lauga (Reference Eloy and Lauga2012) derived optimal ciliary beat waveforms with varying sperm number. Elgeti & Gompper (Reference Elgeti and Gompper2013) numerically studied how ciliary geometrical parameters, such as ciliary spacing and beat direction, affected the properties of metachronal waves. The waves exhibited flow-induced emergence; development of an antiplectic metachronal wave increased the propulsion velocity by more than 3–10-fold compared to in-phase beating. Several studies have also found an antiplectic metachronal wave to be optimal for efficiency (Blake Reference Blake1972; Michelin & Lauga Reference Michelin and Lauga2010; Osterman & Vilfan Reference Osterman and Vilfan2011). To clarify how metachronal waves emerge, several self-sustained oscillator models have been developed. Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2012) presented such a model sustained by a linear elastic spring. It was concluded that orbit compliance mediated by spring elasticity facilitated fast robust synchronisation of two oscillators.
Although earlier studies on squirmers and cilia-driven flow yielded valuable insights into the dynamics of swimming ciliates and the propulsion velocity of metachronal waves, their relationship remains unclear, especially the difference between swimming mediated by surface squirming and ciliary motions. Here, we develop a three-dimensional ciliate model incorporating individual ciliary motions on cell surfaces. We analyse the flow field using a boundary element–slender-body coupling method. This methodology allows us to accurately calculate hydrodynamic interactions between cilia and the cell body under free-swimming conditions. The methodology is detailed in § 2. Ciliate swimming behaviours in terms of beat phase, cilia number and body aspect ratio are discussed in § 3. We use oblique metachronal waves to develop three-dimensional helical trajectories. In § 4, we compare our model ciliates with Lighthill–Blake squirmers, focusing on energy dissipation inside/outside the ciliary envelope. Section 5 provides conclusions.
2 Governing equations and numerical methods
2.1 Boundary integral equation with slender-body theory
Consider a ciliate immersed in an infinite Newtonian liquid of density
![]() $\unicode[STIX]{x1D70C}$
and viscosity
$\unicode[STIX]{x1D70C}$
and viscosity
![]() $\unicode[STIX]{x1D707}$
; the ciliate is propelled via individual ciliary motion. The inertial effect of fluid flow is negligible; the Reynolds numbers scaled by ciliary motion and swimming are markedly lower than 1 (
$\unicode[STIX]{x1D707}$
; the ciliate is propelled via individual ciliary motion. The inertial effect of fluid flow is negligible; the Reynolds numbers scaled by ciliary motion and swimming are markedly lower than 1 (
![]() $Re\ll 1$
). Thus, fluid flow around the ciliate is governed by the Stokes equation. The cell body is modelled as a rigid spheroid from which cilia emerge. As cilia are slender, slender-body theory (Tornberg & Shelly Reference Tornberg and Shelly2004) is applicable when analysing ciliary motion. We parametrise the ciliary centreline using arclength
$Re\ll 1$
). Thus, fluid flow around the ciliate is governed by the Stokes equation. The cell body is modelled as a rigid spheroid from which cilia emerge. As cilia are slender, slender-body theory (Tornberg & Shelly Reference Tornberg and Shelly2004) is applicable when analysing ciliary motion. We parametrise the ciliary centreline using arclength
![]() $s\in [0,L]$
, where
$s\in [0,L]$
, where
![]() $L$
is the ciliary length. The flow field at point
$L$
is the ciliary length. The flow field at point
![]() $\boldsymbol{x}$
located on the
$\boldsymbol{x}$
located on the
![]() $i$
th cilium,
$i$
th cilium,
![]() $\boldsymbol{x}\in s_{i}$
, is given by Pozrikidis (Reference Pozrikidis1992) and Tornberg & Shelly (Reference Tornberg and Shelly2004) as
$\boldsymbol{x}\in s_{i}$
, is given by Pozrikidis (Reference Pozrikidis1992) and Tornberg & Shelly (Reference Tornberg and Shelly2004) as
 $$\begin{eqnarray}\displaystyle \boldsymbol{v}(\boldsymbol{x}) & = & \displaystyle -\frac{1}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}}\int _{cell}\boldsymbol{J}(\boldsymbol{x},\boldsymbol{y})\boldsymbol{\cdot }\boldsymbol{q}(\boldsymbol{y})\,\text{d}A(\boldsymbol{y})-\frac{1}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}}\unicode[STIX]{x1D726}(\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{f}(\boldsymbol{x})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}}\int _{cilia}[\boldsymbol{J}(\boldsymbol{x},\boldsymbol{y})\boldsymbol{\cdot }\boldsymbol{f}(\boldsymbol{y})+\boldsymbol{K}(\boldsymbol{x},\boldsymbol{y})\boldsymbol{\cdot }\boldsymbol{f}(\boldsymbol{x})]\,\text{d}s_{i}(\boldsymbol{y})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}}\mathop{\sum }_{j\neq i}^{N}\int _{cilia}[\boldsymbol{J}(\boldsymbol{x},\boldsymbol{y})+\boldsymbol{W}(\boldsymbol{x},\boldsymbol{y})]\boldsymbol{\cdot }\boldsymbol{f}(\boldsymbol{y})\,\text{d}s_{j}(\boldsymbol{y}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{v}(\boldsymbol{x}) & = & \displaystyle -\frac{1}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}}\int _{cell}\boldsymbol{J}(\boldsymbol{x},\boldsymbol{y})\boldsymbol{\cdot }\boldsymbol{q}(\boldsymbol{y})\,\text{d}A(\boldsymbol{y})-\frac{1}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}}\unicode[STIX]{x1D726}(\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{f}(\boldsymbol{x})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}}\int _{cilia}[\boldsymbol{J}(\boldsymbol{x},\boldsymbol{y})\boldsymbol{\cdot }\boldsymbol{f}(\boldsymbol{y})+\boldsymbol{K}(\boldsymbol{x},\boldsymbol{y})\boldsymbol{\cdot }\boldsymbol{f}(\boldsymbol{x})]\,\text{d}s_{i}(\boldsymbol{y})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}}\mathop{\sum }_{j\neq i}^{N}\int _{cilia}[\boldsymbol{J}(\boldsymbol{x},\boldsymbol{y})+\boldsymbol{W}(\boldsymbol{x},\boldsymbol{y})]\boldsymbol{\cdot }\boldsymbol{f}(\boldsymbol{y})\,\text{d}s_{j}(\boldsymbol{y}),\end{eqnarray}$$
where
![]() $\boldsymbol{q}$
is the viscous traction on the cell body,
$\boldsymbol{q}$
is the viscous traction on the cell body,
![]() $\boldsymbol{f}$
is the force density per unit length and
$\boldsymbol{f}$
is the force density per unit length and
![]() $N$
is the total number of cilia. The first integral on the right operates over the entire spheroidal cell surface, and the second and third integrals operate along the central ciliary lines. The Green’s function
$N$
is the total number of cilia. The first integral on the right operates over the entire spheroidal cell surface, and the second and third integrals operate along the central ciliary lines. The Green’s function
![]() $\boldsymbol{J}$
is given by
$\boldsymbol{J}$
is given by
where
![]() $r=|\boldsymbol{r}|$
and
$r=|\boldsymbol{r}|$
and
![]() $\boldsymbol{r}=\boldsymbol{x}-\boldsymbol{y}$
. In (2.1)
$\boldsymbol{r}=\boldsymbol{x}-\boldsymbol{y}$
. In (2.1)
![]() $\unicode[STIX]{x1D726}$
and
$\unicode[STIX]{x1D726}$
and
![]() $\boldsymbol{K}$
are the local operators of the slender-body theory, which are given by (Tornberg & Shelly Reference Tornberg and Shelly2004)
$\boldsymbol{K}$
are the local operators of the slender-body theory, which are given by (Tornberg & Shelly Reference Tornberg and Shelly2004)
and
where
![]() $c=-\ln (\unicode[STIX]{x1D700}^{2}e)$
,
$c=-\ln (\unicode[STIX]{x1D700}^{2}e)$
,
![]() $\boldsymbol{t}$
is the unit tangential vector to the centreline of each cilium and
$\boldsymbol{t}$
is the unit tangential vector to the centreline of each cilium and
![]() $\unicode[STIX]{x1D700}=a_{cilia}/L$
, with
$\unicode[STIX]{x1D700}=a_{cilia}/L$
, with
![]() $a_{cilia}$
the ciliary radius. In terms of the practical ciliary radius and length ratio (Sleigh Reference Sleigh1962), the slenderness value
$a_{cilia}$
the ciliary radius. In terms of the practical ciliary radius and length ratio (Sleigh Reference Sleigh1962), the slenderness value
![]() $\unicode[STIX]{x1D700}$
is set to
$\unicode[STIX]{x1D700}$
is set to
![]() $\unicode[STIX]{x1D700}=0.01$
throughout the present study. The slender-body kernel
$\unicode[STIX]{x1D700}=0.01$
throughout the present study. The slender-body kernel
![]() $\boldsymbol{W}$
is defined by
$\boldsymbol{W}$
is defined by
When the observation point
![]() $\boldsymbol{x}$
is not on a cilium,
$\boldsymbol{x}$
is not on a cilium,
![]() $\boldsymbol{x}\notin s$
, the velocity is given by
$\boldsymbol{x}\notin s$
, the velocity is given by
 $$\begin{eqnarray}\displaystyle \boldsymbol{v}(\boldsymbol{x}) & = & \displaystyle -\frac{1}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}}\int _{cell}\boldsymbol{J}(\boldsymbol{x},\boldsymbol{y})\boldsymbol{\cdot }\boldsymbol{q}(\boldsymbol{y})\,\text{d}A(\boldsymbol{y})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}}\mathop{\sum }_{j=1}^{N}\int _{cilia}[\boldsymbol{J}(\boldsymbol{x},\boldsymbol{y})+\boldsymbol{W}(\boldsymbol{x},\boldsymbol{y})]\boldsymbol{\cdot }\boldsymbol{f}(\boldsymbol{y})\,\text{d}s_{j}(\boldsymbol{y}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{v}(\boldsymbol{x}) & = & \displaystyle -\frac{1}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}}\int _{cell}\boldsymbol{J}(\boldsymbol{x},\boldsymbol{y})\boldsymbol{\cdot }\boldsymbol{q}(\boldsymbol{y})\,\text{d}A(\boldsymbol{y})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}}\mathop{\sum }_{j=1}^{N}\int _{cilia}[\boldsymbol{J}(\boldsymbol{x},\boldsymbol{y})+\boldsymbol{W}(\boldsymbol{x},\boldsymbol{y})]\boldsymbol{\cdot }\boldsymbol{f}(\boldsymbol{y})\,\text{d}s_{j}(\boldsymbol{y}).\end{eqnarray}$$
Though the asymptotic accuracy of kernels
![]() $\unicode[STIX]{x1D726}$
and
$\unicode[STIX]{x1D726}$
and
![]() $\boldsymbol{K}$
is
$\boldsymbol{K}$
is
![]() $O(\unicode[STIX]{x1D700}^{2}\ln \unicode[STIX]{x1D700})$
, kernel
$O(\unicode[STIX]{x1D700}^{2}\ln \unicode[STIX]{x1D700})$
, kernel
![]() $\boldsymbol{W}$
is accurate only to the limit
$\boldsymbol{W}$
is accurate only to the limit
![]() $O(\unicode[STIX]{x1D700})$
(Tornberg & Shelly Reference Tornberg and Shelly2004). Equations (2.1) and (2.6) are therefore accurate to the limit
$O(\unicode[STIX]{x1D700})$
(Tornberg & Shelly Reference Tornberg and Shelly2004). Equations (2.1) and (2.6) are therefore accurate to the limit
![]() $O(\unicode[STIX]{x1D700})$
.
$O(\unicode[STIX]{x1D700})$
.
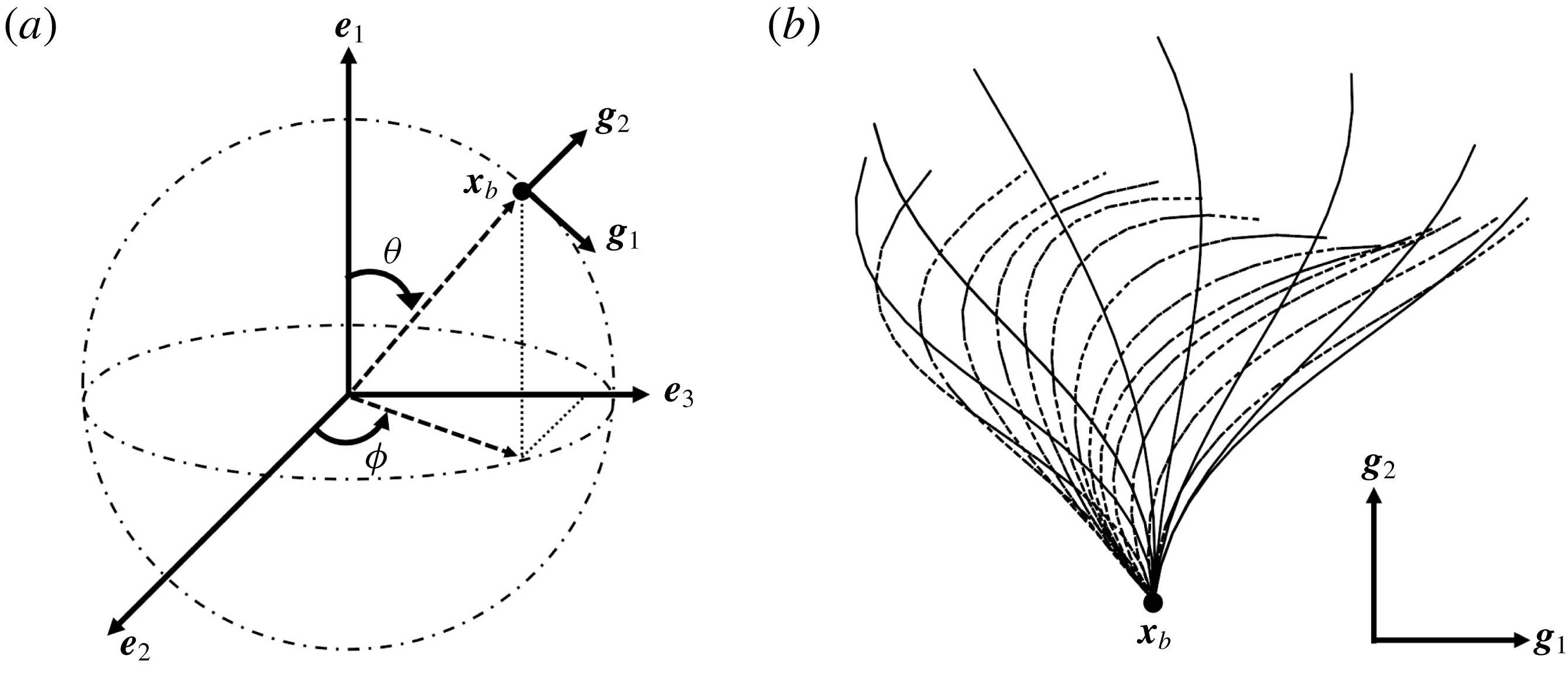
Figure 1. Problem setting. (a) Schematics of the body frames and the angles
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x1D719}$
. (b) Beat pattern of each cilium described by the parameters in table 1.
$\unicode[STIX]{x1D719}$
. (b) Beat pattern of each cilium described by the parameters in table 1.
2.2 Ciliary motions
We first define an orthonormal frame for the cell body
![]() $\boldsymbol{e}_{i}$
with origin
$\boldsymbol{e}_{i}$
with origin
![]() $\boldsymbol{x}_{c}$
, where
$\boldsymbol{x}_{c}$
, where
![]() $\boldsymbol{x}_{c}$
is the body’s centre of mass;
$\boldsymbol{x}_{c}$
is the body’s centre of mass;
![]() $\boldsymbol{e}_{1}$
then reflects swimming orientation. To efficiently model ciliary motion on the cell surface, local vectors with an orthonormal basis
$\boldsymbol{e}_{1}$
then reflects swimming orientation. To efficiently model ciliary motion on the cell surface, local vectors with an orthonormal basis
![]() $\boldsymbol{g}_{i}$
are defined as follows. A material point
$\boldsymbol{g}_{i}$
are defined as follows. A material point
![]() $\boldsymbol{x}_{b}$
, located at the base of a cilium on the cell surface, serves as the origin of the orthonormal body frame
$\boldsymbol{x}_{b}$
, located at the base of a cilium on the cell surface, serves as the origin of the orthonormal body frame
![]() $\boldsymbol{g}_{i}$
(cf. figure 1
a). The basis vectors
$\boldsymbol{g}_{i}$
(cf. figure 1
a). The basis vectors
![]() $\boldsymbol{g}_{1}$
and
$\boldsymbol{g}_{1}$
and
![]() $\boldsymbol{g}_{2}$
are defined as
$\boldsymbol{g}_{2}$
are defined as
![]() $\boldsymbol{g}_{1}(\boldsymbol{x}_{b})=\boldsymbol{b}(\boldsymbol{x}_{b})\wedge \boldsymbol{n}(\boldsymbol{x}_{b})/|\boldsymbol{b}(\boldsymbol{x}_{b})\wedge \boldsymbol{n}(\boldsymbol{x}_{b})|$
and
$\boldsymbol{g}_{1}(\boldsymbol{x}_{b})=\boldsymbol{b}(\boldsymbol{x}_{b})\wedge \boldsymbol{n}(\boldsymbol{x}_{b})/|\boldsymbol{b}(\boldsymbol{x}_{b})\wedge \boldsymbol{n}(\boldsymbol{x}_{b})|$
and
![]() $\boldsymbol{g}_{2}(\boldsymbol{x}_{b})=\boldsymbol{n}(\boldsymbol{x}_{b})$
, where
$\boldsymbol{g}_{2}(\boldsymbol{x}_{b})=\boldsymbol{n}(\boldsymbol{x}_{b})$
, where
![]() $\boldsymbol{b}=\boldsymbol{e}_{1}\wedge \boldsymbol{n}$
and
$\boldsymbol{b}=\boldsymbol{e}_{1}\wedge \boldsymbol{n}$
and
![]() $\boldsymbol{n}$
is the outward unit normal vector, respectively. The time-dependent profile of each ciliary motion is derived using the following mathematical formula of Fulford & Blake (Reference Fulford and Blake1986):
$\boldsymbol{n}$
is the outward unit normal vector, respectively. The time-dependent profile of each ciliary motion is derived using the following mathematical formula of Fulford & Blake (Reference Fulford and Blake1986):
where
with
![]() $\unicode[STIX]{x1D714}$
the angular beat frequency. The Fourier coefficients
$\unicode[STIX]{x1D714}$
the angular beat frequency. The Fourier coefficients
![]() $\unicode[STIX]{x1D6FC}_{n}^{i}$
and
$\unicode[STIX]{x1D6FC}_{n}^{i}$
and
![]() $\unicode[STIX]{x1D6FD}_{n}^{i}$
are given by
$\unicode[STIX]{x1D6FD}_{n}^{i}$
are given by
The coefficients
![]() $A_{mn}^{i}$
and
$A_{mn}^{i}$
and
![]() $B_{mn}^{i}$
are summarised in table 1. In this study, the wavenumbers
$B_{mn}^{i}$
are summarised in table 1. In this study, the wavenumbers
![]() $N_{0}$
and
$N_{0}$
and
![]() $M_{0}$
are set to 3. The beat pattern described by the parameters in table 1 is shown in figure 1(b).
$M_{0}$
are set to 3. The beat pattern described by the parameters in table 1 is shown in figure 1(b).
Table 1. Fourier coefficients for ciliary beating, which are taken from Fulford & Blake (Reference Fulford and Blake1986).
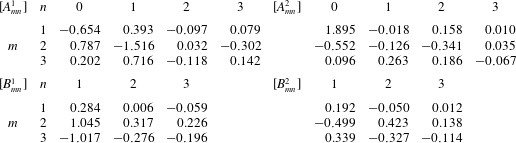
2.3 Boundary element method
In order to simulate free swimming of the ciliate model, force-free and torque-free conditions are taken into account:
and
where
![]() $\hat{\boldsymbol{r}}=\boldsymbol{x}-\boldsymbol{x}_{c}$
, and
$\hat{\boldsymbol{r}}=\boldsymbol{x}-\boldsymbol{x}_{c}$
, and
![]() $\boldsymbol{x}_{c}$
is the centre of mass of the cell body.
$\boldsymbol{x}_{c}$
is the centre of mass of the cell body.
Assuming that the cell body shows a rigid motion, the velocity on the spheroidal cell body surface and on the cilia can be expressed by
where
![]() $\boldsymbol{V}$
is the translational and
$\boldsymbol{V}$
is the translational and
![]() $\unicode[STIX]{x1D734}$
the angular velocity, and
$\unicode[STIX]{x1D734}$
the angular velocity, and
![]() $\boldsymbol{v}^{cilia}$
is the ciliary velocity with respect to the body frame
$\boldsymbol{v}^{cilia}$
is the ciliary velocity with respect to the body frame
![]() $\boldsymbol{e}_{i}$
(i.e.
$\boldsymbol{e}_{i}$
(i.e.
![]() $\boldsymbol{v}^{cilia}=\unicode[STIX]{x2202}\boldsymbol{x}^{cilia}/\unicode[STIX]{x2202}t$
). We then solve the resistance problem with respect to the unknowns
$\boldsymbol{v}^{cilia}=\unicode[STIX]{x2202}\boldsymbol{x}^{cilia}/\unicode[STIX]{x2202}t$
). We then solve the resistance problem with respect to the unknowns
![]() $\boldsymbol{V}$
and
$\boldsymbol{V}$
and
![]() $\unicode[STIX]{x1D734}$
, and derive the viscous tractions
$\unicode[STIX]{x1D734}$
, and derive the viscous tractions
![]() $\boldsymbol{q}$
and
$\boldsymbol{q}$
and
![]() $\boldsymbol{f}$
.
$\boldsymbol{f}$
.
The cell body is modelled as a rigid spheroid, and the body surface is discretised into 5120 triangular mesh elements with 2562 nodal points. Each cilium is discretised into 16 nodes that are interpolated using the centripetal Catmull–Rom spline method (Catmull & Rom Reference Catmull and Rom1974). All physical quantities are computed at each discretised point. The boundary integrals of (2.1) and (2.6) are computed with the aid of numerical Gaussian integration. When an observation point
![]() $\boldsymbol{x}$
is located on the cell body, the following linear algebraic equation can be derived from (2.6):
$\boldsymbol{x}$
is located on the cell body, the following linear algebraic equation can be derived from (2.6):
When
![]() $\boldsymbol{x}$
is on the cilia, on the other hand, we have the following equation from (2.1):
$\boldsymbol{x}$
is on the cilia, on the other hand, we have the following equation from (2.1):
The vector sizes of
![]() $[\boldsymbol{v}^{b}]$
and
$[\boldsymbol{v}^{b}]$
and
![]() $[\boldsymbol{q}]$
are
$[\boldsymbol{q}]$
are
![]() $3N_{b}$
, while
$3N_{b}$
, while
![]() $[\boldsymbol{v}^{c}]$
and
$[\boldsymbol{v}^{c}]$
and
![]() $[\,\boldsymbol{f}]$
have the size
$[\,\boldsymbol{f}]$
have the size
![]() $3N_{c}$
, where
$3N_{c}$
, where
![]() $N_{b}$
is the number of nodes on the cell body and
$N_{b}$
is the number of nodes on the cell body and
![]() $N_{c}$
is the total number of nodes on the cilia. The matrix sizes of
$N_{c}$
is the total number of nodes on the cilia. The matrix sizes of
![]() $[{\mathcal{J}}^{bb}]$
and
$[{\mathcal{J}}^{bb}]$
and
![]() $[{\mathcal{J}}^{bc}]$
are
$[{\mathcal{J}}^{bc}]$
are
![]() $3N_{b}\times 3N_{b}$
and
$3N_{b}\times 3N_{b}$
and
![]() $3N_{b}\times 3N_{c}$
, whereas
$3N_{b}\times 3N_{c}$
, whereas
![]() $[{\mathcal{J}}^{cb}]$
and
$[{\mathcal{J}}^{cb}]$
and
![]() $[{\mathcal{J}}^{cc}]$
are
$[{\mathcal{J}}^{cc}]$
are
![]() $3N_{c}\times 3N_{b}$
and
$3N_{c}\times 3N_{b}$
and
![]() $3N_{c}\times 3N_{c}$
, respectively. In a similar manner, discretised forms of the force–torque conditions, (2.10) and (2.11), can be written as
$3N_{c}\times 3N_{c}$
, respectively. In a similar manner, discretised forms of the force–torque conditions, (2.10) and (2.11), can be written as
and
Considering the boundary condition of (2.12), the system can be expanded to
 $$\begin{eqnarray}\displaystyle \left[\begin{array}{@{}cccc@{}}{\mathcal{J}}^{bb} & {\mathcal{J}}^{bc} & {\mathcal{V}}^{b} & {\mathcal{A}}^{b}\\ {\mathcal{J}}^{cb} & {\mathcal{J}}^{cc} & {\mathcal{V}}^{c} & {\mathcal{A}}^{c}\\ {\mathcal{F}}^{b} & {\mathcal{F}}^{c} & \mathbf{0} & \mathbf{0}\\ {\mathcal{T}}^{b} & {\mathcal{T}}^{c} & \mathbf{0} & \mathbf{0}\end{array}\right]\left[\begin{array}{@{}c@{}}\boldsymbol{q}\\ \boldsymbol{f}\\ \boldsymbol{V}\\ \unicode[STIX]{x1D734}\end{array}\right]=\left[\begin{array}{@{}c@{}}\mathbf{0}\\ \boldsymbol{v}^{cilia}\\ \mathbf{0}\\ \boldsymbol{ 0}\end{array}\right]. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left[\begin{array}{@{}cccc@{}}{\mathcal{J}}^{bb} & {\mathcal{J}}^{bc} & {\mathcal{V}}^{b} & {\mathcal{A}}^{b}\\ {\mathcal{J}}^{cb} & {\mathcal{J}}^{cc} & {\mathcal{V}}^{c} & {\mathcal{A}}^{c}\\ {\mathcal{F}}^{b} & {\mathcal{F}}^{c} & \mathbf{0} & \mathbf{0}\\ {\mathcal{T}}^{b} & {\mathcal{T}}^{c} & \mathbf{0} & \mathbf{0}\end{array}\right]\left[\begin{array}{@{}c@{}}\boldsymbol{q}\\ \boldsymbol{f}\\ \boldsymbol{V}\\ \unicode[STIX]{x1D734}\end{array}\right]=\left[\begin{array}{@{}c@{}}\mathbf{0}\\ \boldsymbol{v}^{cilia}\\ \mathbf{0}\\ \boldsymbol{ 0}\end{array}\right]. & & \displaystyle\end{eqnarray}$$
The matrix components
![]() ${\mathcal{V}}^{b}$
and
${\mathcal{V}}^{b}$
and
![]() ${\mathcal{A}}^{b}$
are of sizes
${\mathcal{A}}^{b}$
are of sizes
![]() $3N_{b}\times 3$
, whereas
$3N_{b}\times 3$
, whereas
![]() ${\mathcal{V}}^{c}$
and
${\mathcal{V}}^{c}$
and
![]() ${\mathcal{A}}^{c}$
are both
${\mathcal{A}}^{c}$
are both
![]() $3N_{c}\times 3$
. The dense matrix (2.17) is solved using the lower–upper (LU) factorisation technique. Given the translational and angular velocities, all material points are updated using the second-order Runge–Kutta method. Validations of the numerical method are shown in appendix A.
$3N_{c}\times 3$
. The dense matrix (2.17) is solved using the lower–upper (LU) factorisation technique. Given the translational and angular velocities, all material points are updated using the second-order Runge–Kutta method. Validations of the numerical method are shown in appendix A.
2.4 Parameter setting
In a Stokes flow regime, the fluid viscosity is simply a multiplier of both force and traction. The viscosity
![]() $\unicode[STIX]{x1D707}$
can be assumed to be unity, without loss of generality. We further assume that all cilia exhibited identical beat frequencies, and beat periodically during computation. To express phase differences among ciliary beats on the cell surface (i.e. metachronal waves), the initial ciliary beat phase
$\unicode[STIX]{x1D707}$
can be assumed to be unity, without loss of generality. We further assume that all cilia exhibited identical beat frequencies, and beat periodically during computation. To express phase differences among ciliary beats on the cell surface (i.e. metachronal waves), the initial ciliary beat phase
![]() $\unicode[STIX]{x1D713}^{0}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
was defined as
$\unicode[STIX]{x1D713}^{0}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D719})$
was defined as
where
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D708}$
are the wavenumbers in the
$\unicode[STIX]{x1D708}$
are the wavenumbers in the
![]() $\unicode[STIX]{x1D703}$
- and
$\unicode[STIX]{x1D703}$
- and
![]() $\unicode[STIX]{x1D719}$
-directions, respectively (cf. figure 1
a). The angle
$\unicode[STIX]{x1D719}$
-directions, respectively (cf. figure 1
a). The angle
![]() $\unicode[STIX]{x1D703}=[0,\unicode[STIX]{x03C0}]$
is that between the orientation vector
$\unicode[STIX]{x1D703}=[0,\unicode[STIX]{x03C0}]$
is that between the orientation vector
![]() $\boldsymbol{e}_{1}$
and
$\boldsymbol{e}_{1}$
and
![]() $\hat{\boldsymbol{r}}_{b}$
; and
$\hat{\boldsymbol{r}}_{b}$
; and
![]() $\unicode[STIX]{x1D703}=\cos ^{-1}(\boldsymbol{e}_{1}\boldsymbol{\cdot }\hat{\boldsymbol{r}}_{b})$
, where
$\unicode[STIX]{x1D703}=\cos ^{-1}(\boldsymbol{e}_{1}\boldsymbol{\cdot }\hat{\boldsymbol{r}}_{b})$
, where
![]() $\hat{\boldsymbol{r}}_{b}=(\boldsymbol{x}_{b}-\boldsymbol{x}_{c})/|\boldsymbol{x}_{b}-\boldsymbol{x}_{c}|$
. The angle
$\hat{\boldsymbol{r}}_{b}=(\boldsymbol{x}_{b}-\boldsymbol{x}_{c})/|\boldsymbol{x}_{b}-\boldsymbol{x}_{c}|$
. The angle
![]() $\unicode[STIX]{x1D719}=[-\unicode[STIX]{x03C0},\unicode[STIX]{x03C0}]$
is defined as
$\unicode[STIX]{x1D719}=[-\unicode[STIX]{x03C0},\unicode[STIX]{x03C0}]$
is defined as
![]() $\unicode[STIX]{x1D719}=\pm \cos ^{-1}(\boldsymbol{e}_{2}\boldsymbol{\cdot }\hat{\boldsymbol{r}}_{b})$
; the sign is determined by the sign of
$\unicode[STIX]{x1D719}=\pm \cos ^{-1}(\boldsymbol{e}_{2}\boldsymbol{\cdot }\hat{\boldsymbol{r}}_{b})$
; the sign is determined by the sign of
![]() $\boldsymbol{e}_{3}\boldsymbol{\cdot }\hat{\boldsymbol{r}}_{b}$
.
$\boldsymbol{e}_{3}\boldsymbol{\cdot }\hat{\boldsymbol{r}}_{b}$
.
In the following sections, the wavenumber
![]() $k$
varies from
$k$
varies from
![]() $-2.0$
to 2.0, and
$-2.0$
to 2.0, and
![]() $\unicode[STIX]{x1D708}$
is fixed at 0 except in § 3.5. If
$\unicode[STIX]{x1D708}$
is fixed at 0 except in § 3.5. If
![]() $k$
is positive, an antiplectic metachronal wave is in play; a symplectic metachronal wave is triggered by a negative
$k$
is positive, an antiplectic metachronal wave is in play; a symplectic metachronal wave is triggered by a negative
![]() $k$
. When
$k$
. When
![]() $k$
is set to zero, all cilia beat in phase. In § 3.5, we consider oblique wave propagation, i.e. dexioplectic/laeoplectic metachronal waves; we set
$k$
is set to zero, all cilia beat in phase. In § 3.5, we consider oblique wave propagation, i.e. dexioplectic/laeoplectic metachronal waves; we set
![]() $\unicode[STIX]{x1D708}\neq 0$
.
$\unicode[STIX]{x1D708}\neq 0$
.
The cell body is modelled by a rigid spheroid of major radius
![]() $a_{0}$
and minor axis
$a_{0}$
and minor axis
![]() $b_{0}$
. To explore the effects of aspect ratio, we considered two cell shapes. First, the cell shape was controlled to hold the volume constant regardless of the aspect ratio
$b_{0}$
. To explore the effects of aspect ratio, we considered two cell shapes. First, the cell shape was controlled to hold the volume constant regardless of the aspect ratio
![]() $\unicode[STIX]{x1D6FC}_{v}$
. Next, the major radius was fixed in various aspect ratio, represented as
$\unicode[STIX]{x1D6FC}_{v}$
. Next, the major radius was fixed in various aspect ratio, represented as
![]() $\unicode[STIX]{x1D6FC}_{l}$
. For all computations, the time interval
$\unicode[STIX]{x1D6FC}_{l}$
. For all computations, the time interval
![]() $\unicode[STIX]{x0394}t$
was set to
$\unicode[STIX]{x0394}t$
was set to
![]() $\unicode[STIX]{x0394}t/T=0.01$
, where
$\unicode[STIX]{x0394}t/T=0.01$
, where
![]() $T$
is the ciliary beat period.
$T$
is the ciliary beat period.
3 Swimming motions induced by ciliary beating
3.1 Spherical ciliates featuring in-phase ciliary beating
We first investigated the swimming of spherical ciliates featuring in-phase ciliary beating. The cell radius
![]() $a_{0}$
was set to
$a_{0}$
was set to
![]() $a_{0}/L=3.0$
, similar to the value exhibited by freshwater ciliates Tetrahymena. The ciliary number was set to
$a_{0}/L=3.0$
, similar to the value exhibited by freshwater ciliates Tetrahymena. The ciliary number was set to
![]() $N=160$
. To reproduce in-phase ciliary beating, the wavenumbers
$N=160$
. To reproduce in-phase ciliary beating, the wavenumbers
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D708}$
in (2.18) were set to zero. The orientation vector was initially set to
$\unicode[STIX]{x1D708}$
in (2.18) were set to zero. The orientation vector was initially set to
![]() $\boldsymbol{e}_{1}=(1.0,0,0)$
; the ciliate swam in the
$\boldsymbol{e}_{1}=(1.0,0,0)$
; the ciliate swam in the
![]() $x$
-direction.
$x$
-direction.
Ciliate configurations during a single ciliary beating phase are shown in figure 2 (see also the supplementary movie). All cilia exhibited periodic effective and recovery strokes; the latter strokes occurred at
![]() $0.25\leqslant t/T\leqslant 0.9$
. When the strokes were effective, the ciliate swam forwards, but the direction of motion was reversed during recovery strokes. Thus, the cell was gradually propelled in the
$0.25\leqslant t/T\leqslant 0.9$
. When the strokes were effective, the ciliate swam forwards, but the direction of motion was reversed during recovery strokes. Thus, the cell was gradually propelled in the
![]() $x$
-direction via periodic back-and-forth movement.
$x$
-direction via periodic back-and-forth movement.
To explore swimming velocity in detail, time changes of swimming velocity over a single period are shown in figure 3(a). In the first quarter period
![]() $0\leqslant t/T\leqslant 0.25$
, ciliary beating was effective, and swimming velocity was maximal at
$0\leqslant t/T\leqslant 0.25$
, ciliary beating was effective, and swimming velocity was maximal at
![]() $t/T\sim 0.1$
. The maximum swimming velocity was approximately
$t/T\sim 0.1$
. The maximum swimming velocity was approximately
![]() $V_{x}T/L\simeq 3.0$
, equivalent to a half-body-length per period. During the recovery phase, the velocity was negative, and the ciliate reversed its progress (thus in the minus
$V_{x}T/L\simeq 3.0$
, equivalent to a half-body-length per period. During the recovery phase, the velocity was negative, and the ciliate reversed its progress (thus in the minus
![]() $x$
-direction). Although back-and-forth movement was in play, the total displacement
$x$
-direction). Although back-and-forth movement was in play, the total displacement
![]() $u_{x}=\int _{0}^{T}V_{x}\,\text{d}t$
was positive; the ciliate moved forwards.
$u_{x}=\int _{0}^{T}V_{x}\,\text{d}t$
was positive; the ciliate moved forwards.
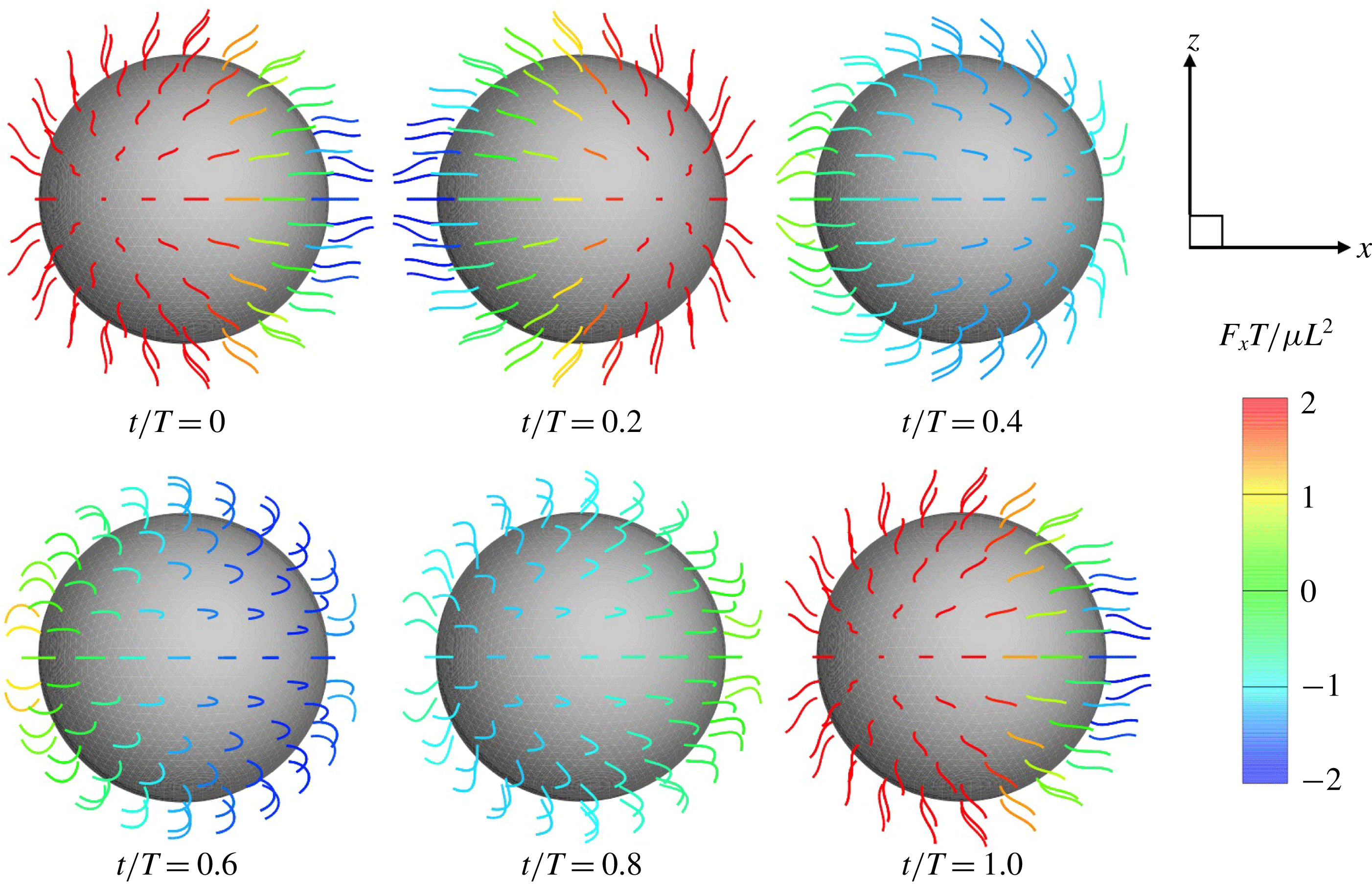
Figure 2. Swimming of the spherical ciliate during one period (
![]() $N=160$
,
$N=160$
,
![]() $a_{0}/L=3.0$
and in-phase beating). The colour on the cilia indicates the propulsion force of individual cilia calculated by
$a_{0}/L=3.0$
and in-phase beating). The colour on the cilia indicates the propulsion force of individual cilia calculated by
![]() $\int f_{x}\,\text{d}s$
. A movie can be seen in the supplemental material available at https://doi.org/10.1017/jfm.2019.490.
$\int f_{x}\,\text{d}s$
. A movie can be seen in the supplemental material available at https://doi.org/10.1017/jfm.2019.490.

Figure 3. (a) Swimming velocity of the ciliate as a function of time. (b) Propulsion force of individual cilia in three regions calculated by
![]() $\sum _{i}\int f_{x}\,\text{d}s_{i}$
. Regions A, B and C are posterior, middle and anterior regions, as shown in the inset.
$\sum _{i}\int f_{x}\,\text{d}s_{i}$
. Regions A, B and C are posterior, middle and anterior regions, as shown in the inset.
In figure 2, all cilia beat in-phase, but the contributions of individual cilia to swimming velocity depended on ciliary position. The contour colours of the ciliary surface indicate propulsion afforded by ciliary motion, i.e. the
![]() $\int f_{x}\,\text{d}s$
values. Red suggests that the cell is pushed forwards by ciliary motion, and blue that the cell is forced back by such motion. For example, at
$\int f_{x}\,\text{d}s$
values. Red suggests that the cell is pushed forwards by ciliary motion, and blue that the cell is forced back by such motion. For example, at
![]() $t/T=0.0$
, the anterior cilia are blue, suggesting that locomotion was compromised. Both posterior and central cilia can trigger locomotion. In figure 3(b), the propulsion forces generated in three regions are shown. Region A represents the posterior area (encompassing one-third of the body from the posterior end). Regions B and C are the middle and anterior regions (each encompassing one-third of the body length, as shown in the inset). In figure 3(b), it is apparent that the locomotion curves of different ciliary positions vary, and that the locomotion peak shifts from region A to C over time. The total force curve is similar to the swimming velocity curve; the total ciliate drag is not affected by ciliary configuration.
$t/T=0.0$
, the anterior cilia are blue, suggesting that locomotion was compromised. Both posterior and central cilia can trigger locomotion. In figure 3(b), the propulsion forces generated in three regions are shown. Region A represents the posterior area (encompassing one-third of the body from the posterior end). Regions B and C are the middle and anterior regions (each encompassing one-third of the body length, as shown in the inset). In figure 3(b), it is apparent that the locomotion curves of different ciliary positions vary, and that the locomotion peak shifts from region A to C over time. The total force curve is similar to the swimming velocity curve; the total ciliate drag is not affected by ciliary configuration.
3.2 Effect of metachronal wave
Elgeti & Gompper (Reference Elgeti and Gompper2013) investigated the emergence of metachronal waves in ciliary arrays active on a flat plane, and concluded that such waves increased propulsion velocity. Thus, even when the cell body is spherical, metachronal waves may enhance swimming velocity. We thus investigated the effects of such waves on cellular locomotion. Here, the aspect ratio was set to 1.0, the ciliary radius to
![]() $a_{0}/L=3.0$
, and the ciliary number to
$a_{0}/L=3.0$
, and the ciliary number to
![]() $N=160$
.
$N=160$
.

Figure 4. Swimming of the ciliate with different initial phase difference
![]() $k$
. By setting positive
$k$
. By setting positive
![]() $k$
, the ciliate shows antiplectic metachronal waves, while negative
$k$
, the ciliate shows antiplectic metachronal waves, while negative
![]() $k$
represents symplectic metachronal wave. The other parameters are the same as in figure 2.
$k$
represents symplectic metachronal wave. The other parameters are the same as in figure 2.
We first examined the effects of an antiplectic metachronal wave. The wavenumbers
![]() $k$
were set to
$k$
were set to
![]() $k=0,~0.5,~1.0$
and 2.0; and
$k=0,~0.5,~1.0$
and 2.0; and
![]() $\unicode[STIX]{x1D708}$
to zero. The ciliate configurations at
$\unicode[STIX]{x1D708}$
to zero. The ciliate configurations at
![]() $k=1.0$
are shown in figure 4. The effective beat is propagated from posterior to anterior over time. The temporal swimming velocities during periods with various wavenumbers
$k=1.0$
are shown in figure 4. The effective beat is propagated from posterior to anterior over time. The temporal swimming velocities during periods with various wavenumbers
![]() $k$
are shown in figure 5(a). When
$k$
are shown in figure 5(a). When
![]() $k=0$
(i.e. during in-phase beating), the swimming velocities (both forwards and backwards) are maximised. When an antiplectic metachronal wave forms (
$k=0$
(i.e. during in-phase beating), the swimming velocities (both forwards and backwards) are maximised. When an antiplectic metachronal wave forms (
![]() $k>0$
), the peak is lower than that associated with in-phase beating, but the effective phase time tends to be longer, as shown in figure 5(a). Time-averaged velocities
$k>0$
), the peak is lower than that associated with in-phase beating, but the effective phase time tends to be longer, as shown in figure 5(a). Time-averaged velocities
![]() $\bar{V}_{x}$
at various
$\bar{V}_{x}$
at various
![]() $k$
-values are shown in figure 5(b);
$k$
-values are shown in figure 5(b);
![]() $\bar{V}_{x}$
is maximum when
$\bar{V}_{x}$
is maximum when
![]() $k\simeq 1.0$
, suggesting that an antiplectic metachronal wave with
$k\simeq 1.0$
, suggesting that an antiplectic metachronal wave with
![]() $k=1.0$
is optimal in this cellular configuration.
$k=1.0$
is optimal in this cellular configuration.
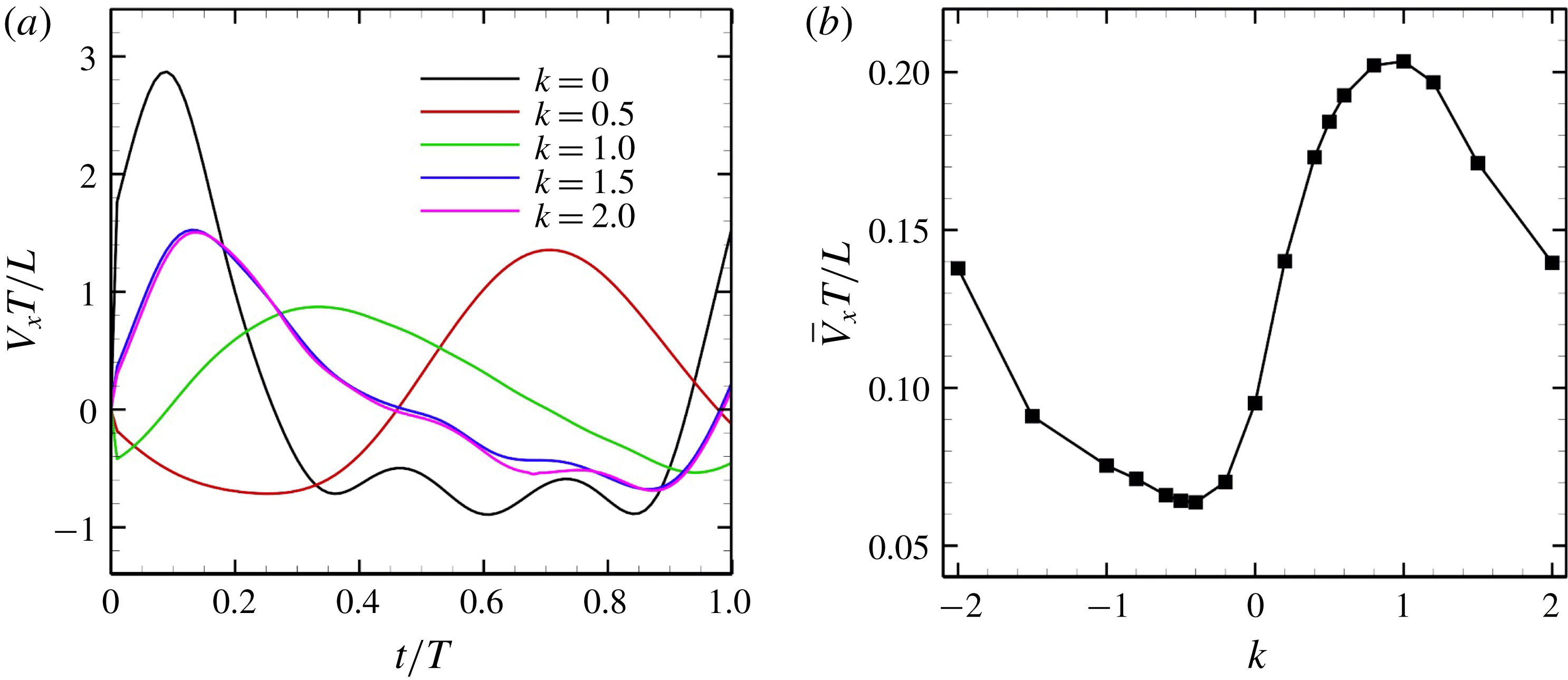
Figure 5. Swimming velocity with various
![]() $k$
. (a) Time change of swimming velocity, and (b) time-averaged swimming speed. When
$k$
. (a) Time change of swimming velocity, and (b) time-averaged swimming speed. When
![]() $k>0$
, the ciliate shows antiplectic metachronal waves, whereas it shows symplectic metachronal waves with
$k>0$
, the ciliate shows antiplectic metachronal waves, whereas it shows symplectic metachronal waves with
![]() $k<0$
. Movies of
$k<0$
. Movies of
![]() $k=1$
and
$k=1$
and
![]() $k=-1$
are available in the supplementary material.
$k=-1$
are available in the supplementary material.
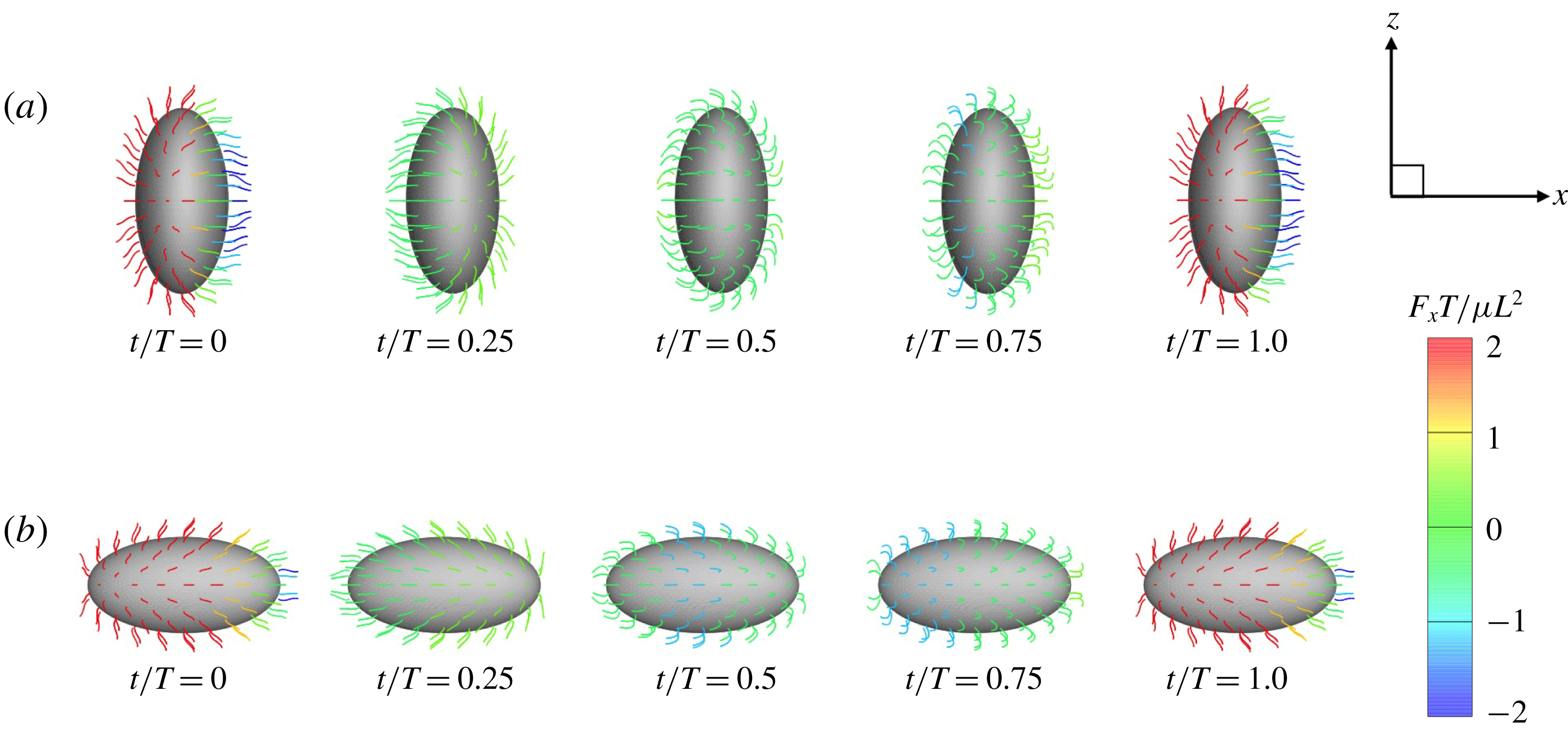
Figure 6. Swimming of spheroidal ciliates: (a) oblate-type ciliate with aspect ratio
![]() $\unicode[STIX]{x1D6FC}_{v}=0.5$
and (b) prolate-type ciliate with
$\unicode[STIX]{x1D6FC}_{v}=0.5$
and (b) prolate-type ciliate with
![]() $\unicode[STIX]{x1D6FC}_{v}=2.0$
. In both cases, ciliary beats are in-phase.
$\unicode[STIX]{x1D6FC}_{v}=2.0$
. In both cases, ciliary beats are in-phase.
We also investigated the effect of a symplectic metachronal wave (i.e.
![]() $k<0$
); the results are also shown in figure 5. Unlike what was seen when an antiplectic wave was in play, swimming velocity was not enhanced by a symplectic metachronal wave. With such a wave, ciliary stroke effectiveness is likely to be compromised by cilia of the posterior side, as shown in figure 4. On the other hand, when an antiplectic wave forms, the distance between the fore and aft cilia engaging in effective strokes becomes larger, and fluid flows freely in the ciliary layer. This agrees well with the findings of earlier studies (Blake Reference Blake1972; Guo et al.
Reference Guo, Nawroth, Ding and Kanso2014). Thus, an antiplectic metachronal wave enhances the swimming velocity of spherical ciliates.
$k<0$
); the results are also shown in figure 5. Unlike what was seen when an antiplectic wave was in play, swimming velocity was not enhanced by a symplectic metachronal wave. With such a wave, ciliary stroke effectiveness is likely to be compromised by cilia of the posterior side, as shown in figure 4. On the other hand, when an antiplectic wave forms, the distance between the fore and aft cilia engaging in effective strokes becomes larger, and fluid flows freely in the ciliary layer. This agrees well with the findings of earlier studies (Blake Reference Blake1972; Guo et al.
Reference Guo, Nawroth, Ding and Kanso2014). Thus, an antiplectic metachronal wave enhances the swimming velocity of spherical ciliates.
3.3 Effect of aspect ratio
In previous sections, the cell considered was spherical, like the micro-alga Volvox. In nature, however, micro-organisms assume various forms. For example, Tetrahymena is ellipsoidal with an aspect ratio of approximately 2. We thus investigated the effects of cellular shape by varying the aspect ratio. As explained in § 2.4, we defined two aspect ratios
![]() $\unicode[STIX]{x1D6FC}_{v}$
and
$\unicode[STIX]{x1D6FC}_{v}$
and
![]() $\unicode[STIX]{x1D6FC}_{l}$
. The swimming behaviours of an oblate ciliate (
$\unicode[STIX]{x1D6FC}_{l}$
. The swimming behaviours of an oblate ciliate (
![]() $\unicode[STIX]{x1D6FC}_{v}=0.5$
) and a prolate ciliate (
$\unicode[STIX]{x1D6FC}_{v}=0.5$
) and a prolate ciliate (
![]() $\unicode[STIX]{x1D6FC}_{v}=2.0$
) are shown in figure 6. For an oblate ciliate, the effective strokes of the anterior and posterior cilia are probably perpendicular to the direction of swimming. Thus, the average swimming velocity is smaller than that of prolate ciliates for both the
$\unicode[STIX]{x1D6FC}_{v}=2.0$
) are shown in figure 6. For an oblate ciliate, the effective strokes of the anterior and posterior cilia are probably perpendicular to the direction of swimming. Thus, the average swimming velocity is smaller than that of prolate ciliates for both the
![]() $\unicode[STIX]{x1D6FC}_{v}$
and
$\unicode[STIX]{x1D6FC}_{v}$
and
![]() $\unicode[STIX]{x1D6FC}_{l}$
cases, as shown in figures 7(a) and 8. When the aspect ratio was varied while keeping the volume constant, the drag coefficient of a rigid spheroid became the minimum when
$\unicode[STIX]{x1D6FC}_{l}$
cases, as shown in figures 7(a) and 8. When the aspect ratio was varied while keeping the volume constant, the drag coefficient of a rigid spheroid became the minimum when
![]() $\unicode[STIX]{x1D6FC}_{v}\sim 2$
, as shown in figure 7(b). Thus, large velocities were observed around
$\unicode[STIX]{x1D6FC}_{v}\sim 2$
, as shown in figure 7(b). Thus, large velocities were observed around
![]() $\unicode[STIX]{x1D6FC}_{v}=2$
in the antiplectic mode. The highest velocities appear at the aspect ratio of approximately 1.5 with
$\unicode[STIX]{x1D6FC}_{v}=2$
in the antiplectic mode. The highest velocities appear at the aspect ratio of approximately 1.5 with
![]() $k=0.5$
–1.5. Hence, the velocity is not simply a function of aspect ratio, but hydrodynamic interactions between cilia play an important role. For
$k=0.5$
–1.5. Hence, the velocity is not simply a function of aspect ratio, but hydrodynamic interactions between cilia play an important role. For
![]() $\unicode[STIX]{x1D6FC}_{l}$
(i.e. the major axis is constant), the cellular volume becomes smaller as the aspect ratio increases and the drag on the cell body thus decreases. Accordingly, the swimming speed increases with
$\unicode[STIX]{x1D6FC}_{l}$
(i.e. the major axis is constant), the cellular volume becomes smaller as the aspect ratio increases and the drag on the cell body thus decreases. Accordingly, the swimming speed increases with
![]() $\unicode[STIX]{x1D6FC}_{l}$
in the moderate-aspect-ratio regime, as shown in figure 8.
$\unicode[STIX]{x1D6FC}_{l}$
in the moderate-aspect-ratio regime, as shown in figure 8.
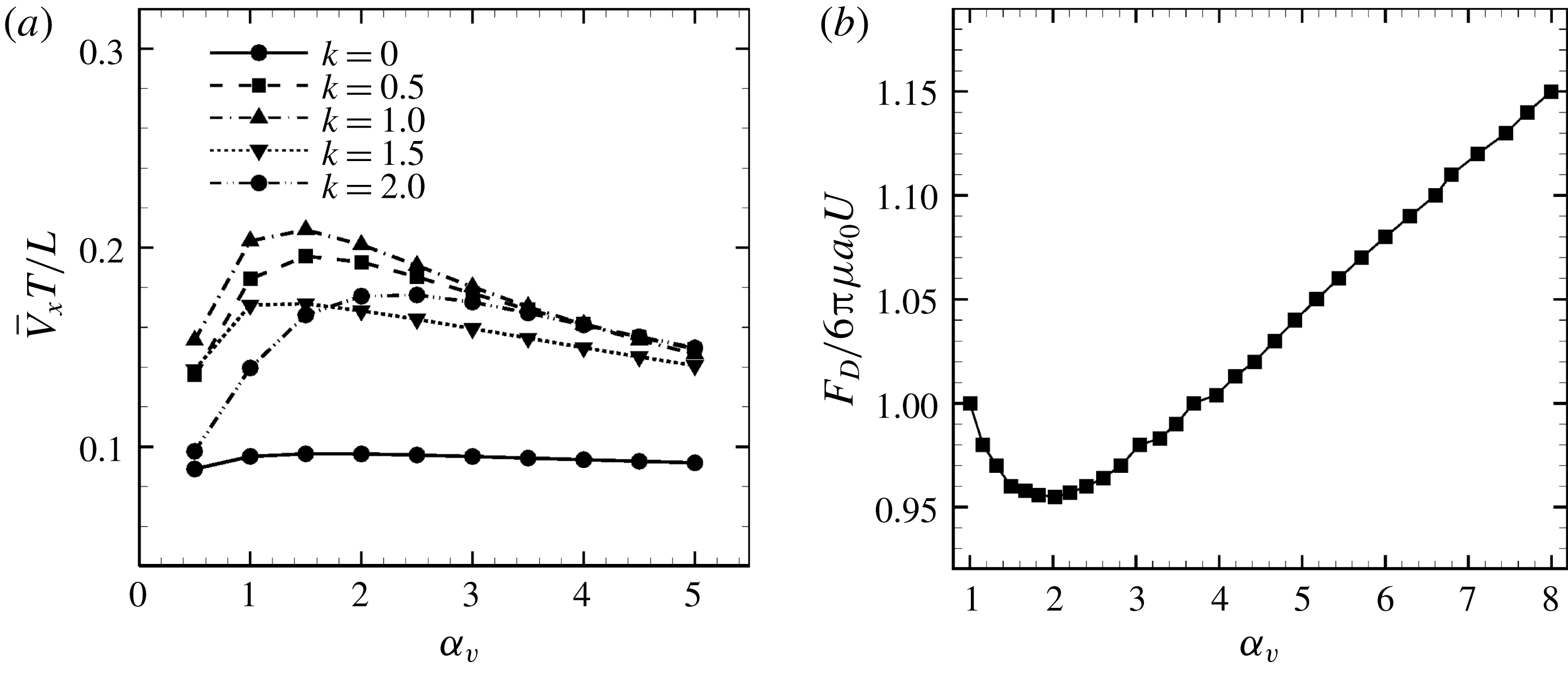
Figure 7. Effect of aspect ratio
![]() $\unicode[STIX]{x1D6FC}_{v}$
so as to keep the volume constant. (a) Average swimming speed of ciliate. For all cases, cilia beat as in-phase and number of cilia
$\unicode[STIX]{x1D6FC}_{v}$
so as to keep the volume constant. (a) Average swimming speed of ciliate. For all cases, cilia beat as in-phase and number of cilia
![]() $N=160$
. (b) Drag coefficient of a rigid spheroid without cilia as a function of
$N=160$
. (b) Drag coefficient of a rigid spheroid without cilia as a function of
![]() $\unicode[STIX]{x1D6FC}_{v}$
. Here
$\unicode[STIX]{x1D6FC}_{v}$
. Here
![]() $U$
is the fluid velocity relative to the rigid spheroid.
$U$
is the fluid velocity relative to the rigid spheroid.
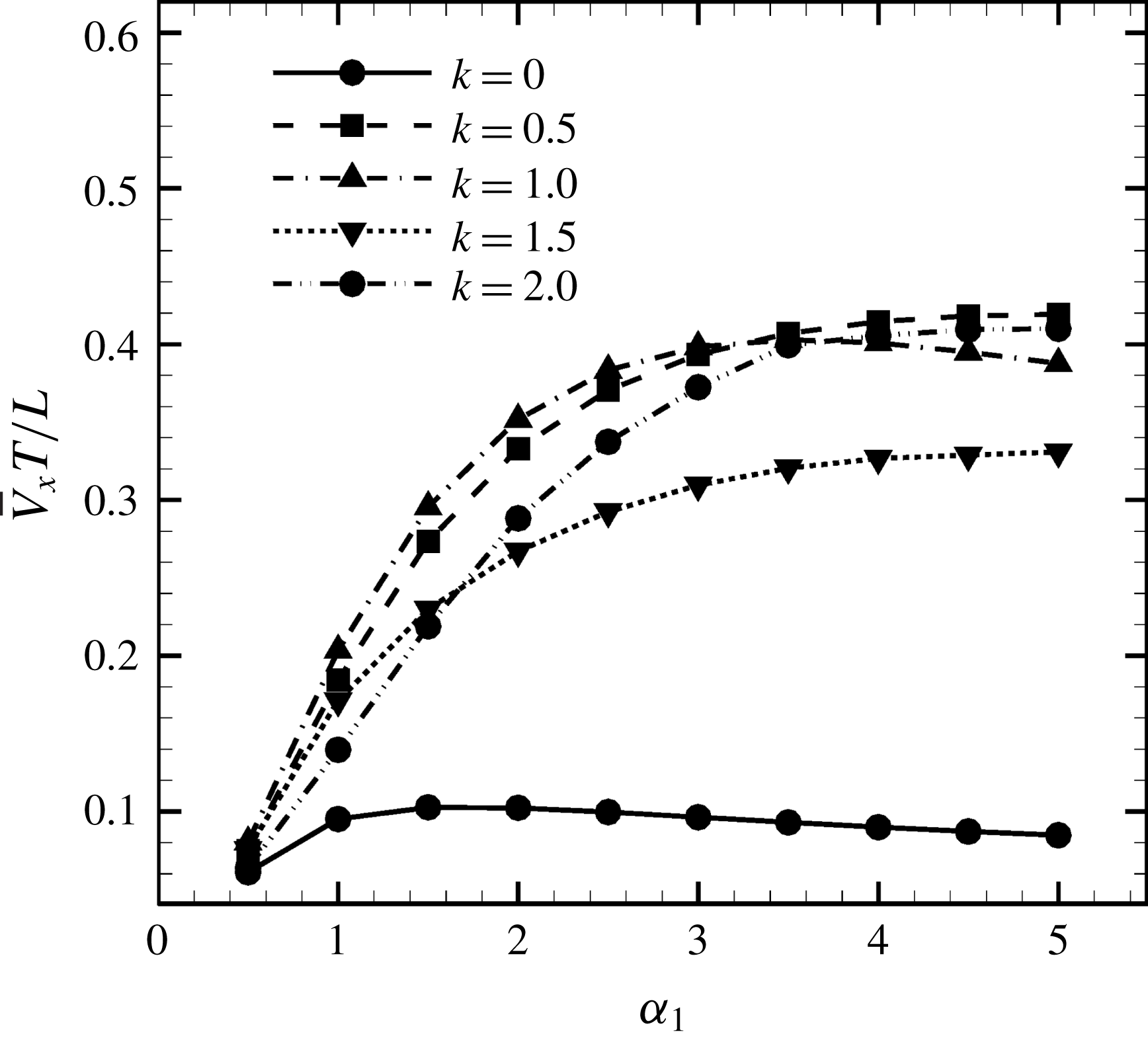
Figure 8. Effect of aspect ratio
![]() $\unicode[STIX]{x1D6FC}_{l}$
so as to keep the major axis constant.
$\unicode[STIX]{x1D6FC}_{l}$
so as to keep the major axis constant.
We compared our results with the swimming behaviour of a real ciliate Tetrahymena. In Ishikawa & Kikuchi (Reference Ishikawa and Kikuchi2018), the aspect ratio of Tetrahymena was found to be approximately 2.1. The body length was approximately
![]() $65~\unicode[STIX]{x03BC}\text{m}$
and the swimming velocity was
$65~\unicode[STIX]{x03BC}\text{m}$
and the swimming velocity was
![]() $440~\unicode[STIX]{x03BC}\text{m}~\text{s}^{-1}$
(i.e. 6.8 body lengths per second). In figure 7(b), the average velocity when
$440~\unicode[STIX]{x03BC}\text{m}~\text{s}^{-1}$
(i.e. 6.8 body lengths per second). In figure 7(b), the average velocity when
![]() $\unicode[STIX]{x1D6FC}_{l}=2.0$
and
$\unicode[STIX]{x1D6FC}_{l}=2.0$
and
![]() $k=1.0$
was approximately 0.35, corresponding to 0.058 body lengths per beat. The beat frequency of Tetrahymena was reported to be approximately 30 Hz (Ishikawa & Kikuchi Reference Ishikawa and Kikuchi2018). Our ciliate model yields a swimming velocity of 1.74 body lengths per second, thus approximately 3.9-fold less than the actual swimming velocity of Tetrahymena. The real Tetrahymena has more than 1000 cilia, whereas our model features only 160 cilia. We thus explored the effect of cilia numbers on swimming velocity.
$k=1.0$
was approximately 0.35, corresponding to 0.058 body lengths per beat. The beat frequency of Tetrahymena was reported to be approximately 30 Hz (Ishikawa & Kikuchi Reference Ishikawa and Kikuchi2018). Our ciliate model yields a swimming velocity of 1.74 body lengths per second, thus approximately 3.9-fold less than the actual swimming velocity of Tetrahymena. The real Tetrahymena has more than 1000 cilia, whereas our model features only 160 cilia. We thus explored the effect of cilia numbers on swimming velocity.
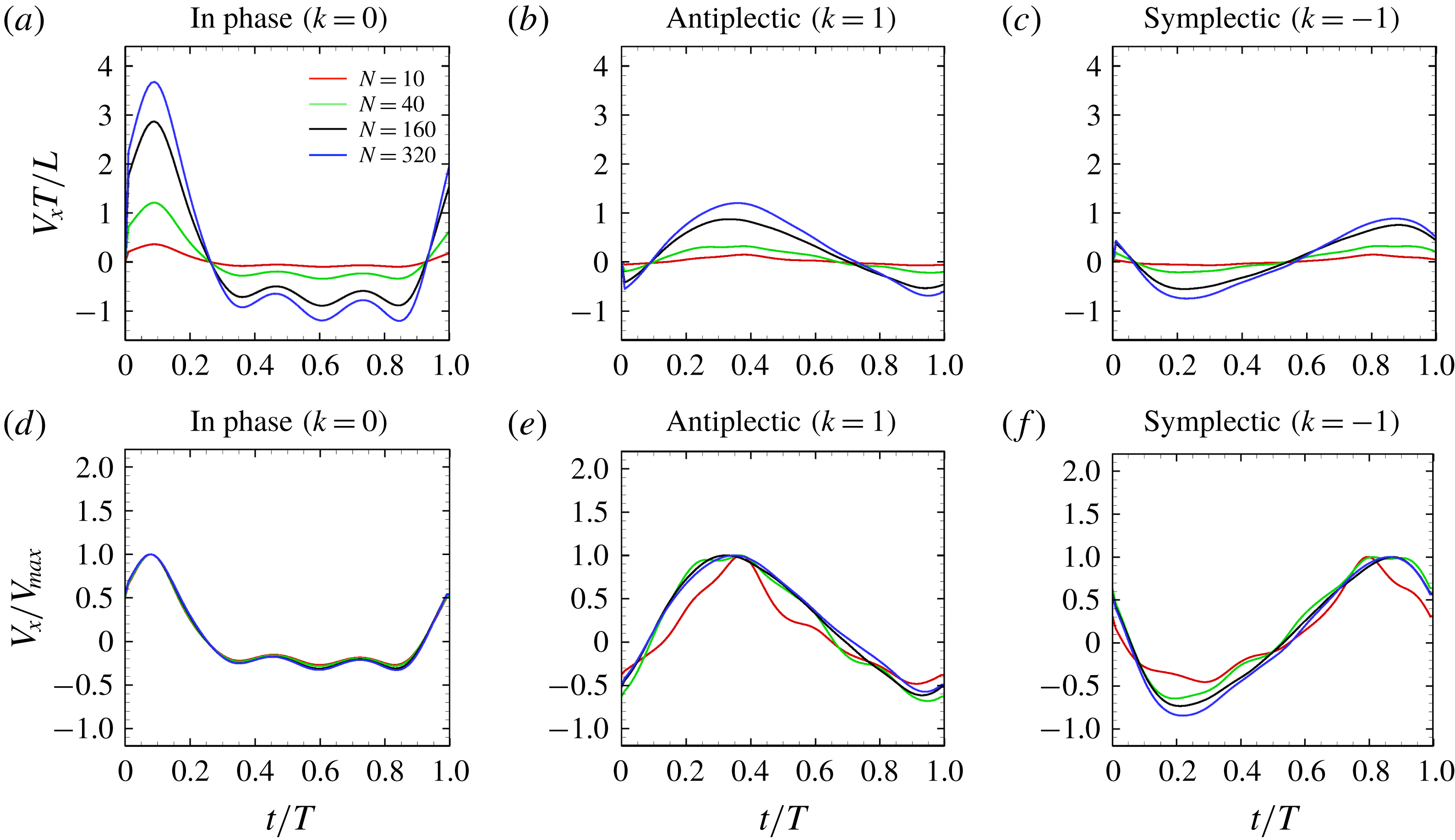
Figure 9. Swimming velocity with different number of cilia and metachronal waves: (a) in-phase, (b) antiplectic and (c) symplectic waves. In panels (d–f), the velocities are normalised by each maximum swimming velocity. For all the cases, we set the aspect ratio equal to 1.0.
3.4 Effect of cilia numbers
Here, we investigate the effect of cilia numbers. The aspect ratio was again set to 1.0 and the radius to
![]() $a_{0}/L=3.0$
. The temporal swimming velocities for
$a_{0}/L=3.0$
. The temporal swimming velocities for
![]() $N=10,~40,~160$
and 320 are shown in figure 9. The wavenumber
$N=10,~40,~160$
and 320 are shown in figure 9. The wavenumber
![]() $k$
was set to
$k$
was set to
![]() $k=-1,~0$
and 1, and
$k=-1,~0$
and 1, and
![]() $\unicode[STIX]{x1D708}$
was set to zero. In the case of
$\unicode[STIX]{x1D708}$
was set to zero. In the case of
![]() $k=0$
, i.e. in-phase beating, the cell showed larger back-and-forth movements as
$k=0$
, i.e. in-phase beating, the cell showed larger back-and-forth movements as
![]() $N$
increases; while in the antiplectic waves, we see a longer period of propelled motions. The maximum instantaneous swimming velocity attains
$N$
increases; while in the antiplectic waves, we see a longer period of propelled motions. The maximum instantaneous swimming velocity attains
![]() $V_{x}T/L\simeq 3.7$
when
$V_{x}T/L\simeq 3.7$
when
![]() $N=320$
at in-phase beating, and was
$N=320$
at in-phase beating, and was
![]() $V_{x}T/L\simeq 3.0$
when
$V_{x}T/L\simeq 3.0$
when
![]() $N=160$
. Thus, the maximum swimming velocity was not simply proportional to the number of cilia. However, when the velocity was normalised by the maximum velocity, all curves almost converged onto one curve regardless of the number of cilia. Thus, the shape of velocity over time is independent of
$N=160$
. Thus, the maximum swimming velocity was not simply proportional to the number of cilia. However, when the velocity was normalised by the maximum velocity, all curves almost converged onto one curve regardless of the number of cilia. Thus, the shape of velocity over time is independent of
![]() $N$
, but it depends on the metachronal waves. We next explored average ciliate velocity as a function of the number of cilia
$N$
, but it depends on the metachronal waves. We next explored average ciliate velocity as a function of the number of cilia
![]() $N$
(cf. figure 10). The swimming velocity increased monotonically with
$N$
(cf. figure 10). The swimming velocity increased monotonically with
![]() $N$
for all
$N$
for all
![]() $k$
, although the slope decreased as
$k$
, although the slope decreased as
![]() $N$
increased. Again, the wavenumber
$N$
increased. Again, the wavenumber
![]() $k=1.0$
was associated with the maximum velocity regardless of the
$k=1.0$
was associated with the maximum velocity regardless of the
![]() $N$
-value. Thus, the optimal wavenumber is not greatly affected by cilia numbers.
$N$
-value. Thus, the optimal wavenumber is not greatly affected by cilia numbers.
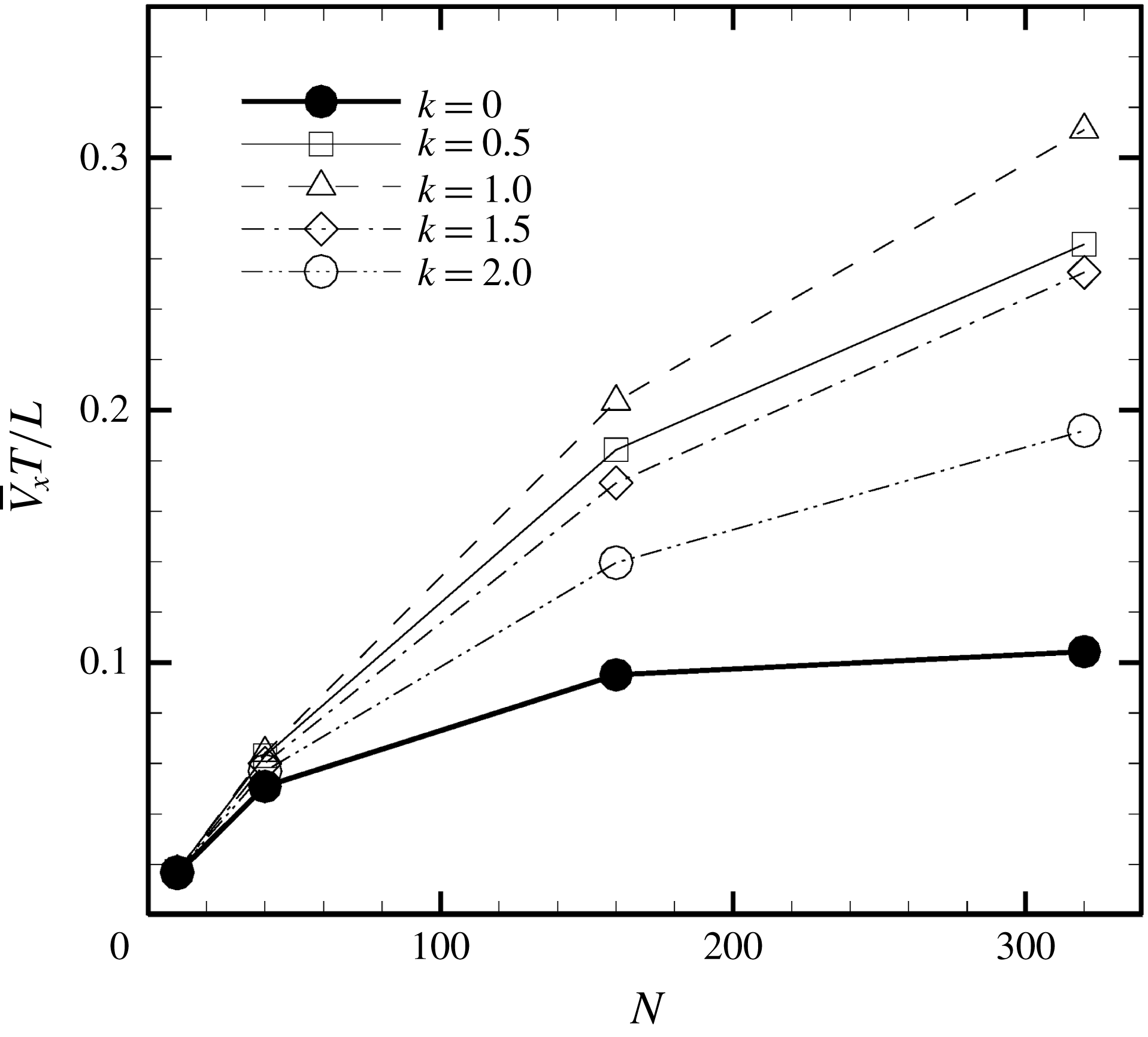
Figure 10. Average swimming velocity with different number of cilia
![]() $N$
.
$N$
.
If hydrodynamic interactions among cilia are omitted, the cilia-driven velocity and the thrust force may be proportional to the number of cilia
![]() $N$
. Using resistive force theory, the force generated by a single cilium
$N$
. Using resistive force theory, the force generated by a single cilium
![]() $F$
can be scaled as (Osterman & Vilfan Reference Osterman and Vilfan2011)
$F$
can be scaled as (Osterman & Vilfan Reference Osterman and Vilfan2011)
where
![]() $\unicode[STIX]{x1D714}$
is the angular velocity of ciliary beat,
$\unicode[STIX]{x1D714}$
is the angular velocity of ciliary beat,
![]() $L$
is the length of the cilium,
$L$
is the length of the cilium,
![]() $c_{N}=4\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}/(\ln (2L/r)-0.5)$
is the drag coefficient of a slender body (Blake Reference Blake1974),
$c_{N}=4\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}/(\ln (2L/r)-0.5)$
is the drag coefficient of a slender body (Blake Reference Blake1974),
![]() $\unicode[STIX]{x1D707}$
is the viscosity and
$\unicode[STIX]{x1D707}$
is the viscosity and
![]() $r$
is the radius of the cilium. The swimming velocity of a spherical ciliate without hydrodynamic interaction can then be scaled as
$r$
is the radius of the cilium. The swimming velocity of a spherical ciliate without hydrodynamic interaction can then be scaled as
The above scaling can be used only for small numbers of cilia and is qualitatively different from the numerical results in figure 10. These results illustrate that hydrodynamic interactions between cilia and the cell body considerably affect swimming velocity.
3.5 Helical swimming with an oblique metachronal wave
Oblique metachronal waves (dexioplectic or laeoplectic waves) are evident in the natural world. To determine the effects of such waves, we considered wave propagations in both the
![]() $\unicode[STIX]{x1D703}$
- and
$\unicode[STIX]{x1D703}$
- and
![]() $\unicode[STIX]{x1D719}$
-directions on a spherical cellular surface. By setting
$\unicode[STIX]{x1D719}$
-directions on a spherical cellular surface. By setting
![]() $\unicode[STIX]{x1D708}=1.0$
and
$\unicode[STIX]{x1D708}=1.0$
and
![]() $k=1.0$
, we established dexioplectic wave propagation; the trajectory of the centre of mass over 10 beats is shown in figure 11. The trajectory is helical, because the ciliary beat is no longer instantaneously axisymmetric, although the time-averaged ciliary propulsion force remains axisymmetric. Thus, helical swimming was reproduced using an oblique metachronal wave even when both the cellular body and time-averaged ciliary propulsion force were axisymmetric.
$k=1.0$
, we established dexioplectic wave propagation; the trajectory of the centre of mass over 10 beats is shown in figure 11. The trajectory is helical, because the ciliary beat is no longer instantaneously axisymmetric, although the time-averaged ciliary propulsion force remains axisymmetric. Thus, helical swimming was reproduced using an oblique metachronal wave even when both the cellular body and time-averaged ciliary propulsion force were axisymmetric.
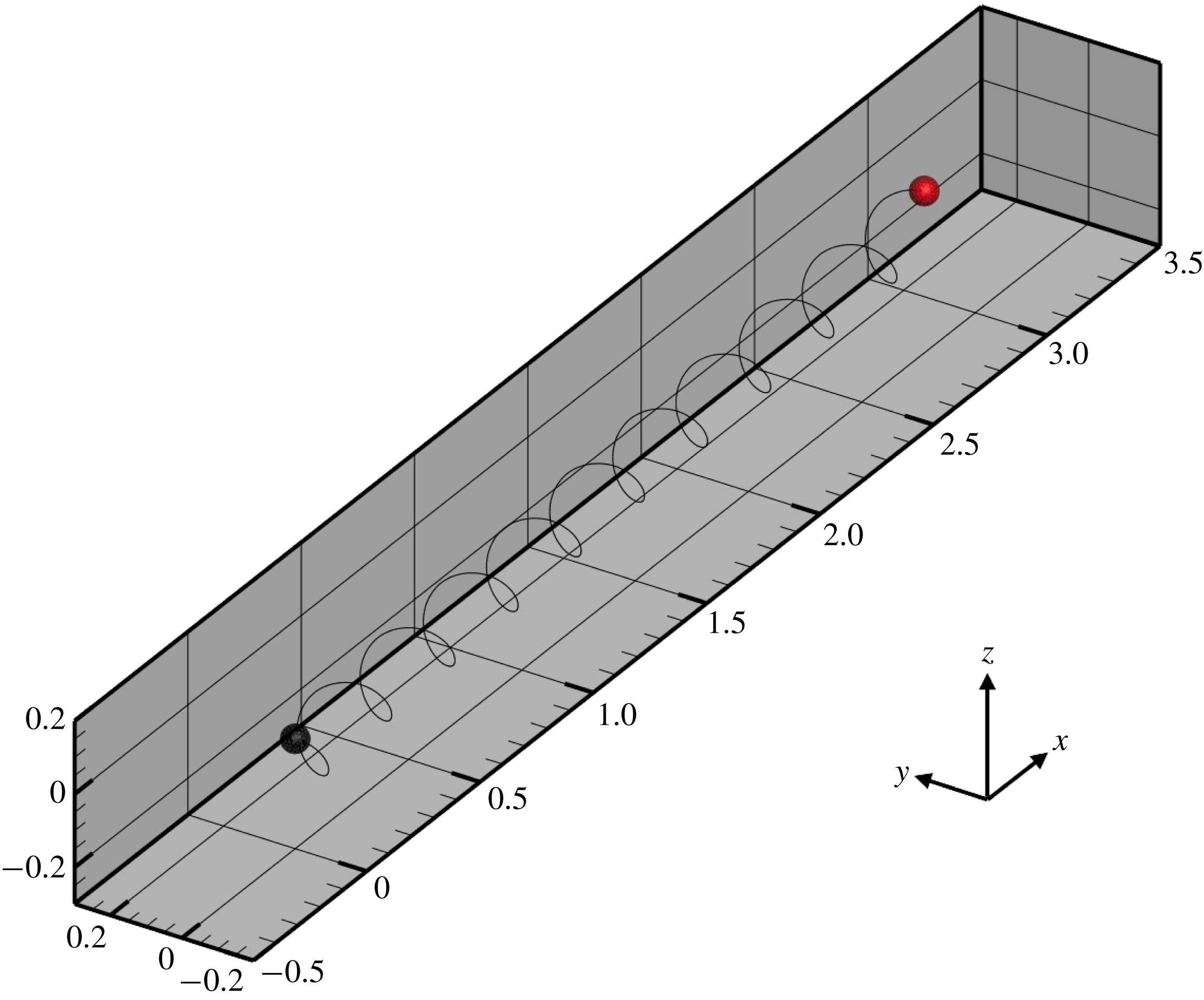
Figure 11. Trajectory of the centre of the spherical ciliate with dexioplectic metachronal wave (
![]() $k=1.0$
and
$k=1.0$
and
![]() $\unicode[STIX]{x1D708}=1.0$
). Black dot indicates starting point, while red dot is the end point. A movie can be seen in the supplementary material.
$\unicode[STIX]{x1D708}=1.0$
). Black dot indicates starting point, while red dot is the end point. A movie can be seen in the supplementary material.
4 Comparison with the Lighthill–Blake squirmer
4.1 Swimming velocity
Here we compare the swimming velocity calculated in the present study to that of the squirmer model. The Lighthill–Blake squirmer (Blake Reference Blake1971) has been widely used in earlier analytical and numerical studies, as mentioned above in § 1. Using spherical polar coordinates, fluid motion caused by squirming in the radial and azimuthal directions is given by
 $$\begin{eqnarray}\displaystyle v_{r}(r,\unicode[STIX]{x1D703}) & = & \displaystyle -U\cos \unicode[STIX]{x1D703}+A_{0}\frac{a^{2}}{r^{2}}P_{0}+\frac{2}{3}(A_{1}+B_{1})\frac{a^{3}}{r^{3}}P_{1}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n=2}^{\infty }\left[\left(\frac{1}{2}n\frac{a^{n}}{r^{n}}-\left(\frac{1}{2}n-1\right)\frac{a^{n+2}}{r^{n+2}}\right)A_{n}P_{n}+\left(\frac{a^{n+2}}{r^{n+2}}-\frac{a^{n}}{r^{n}}\right)B_{n}P_{n}\right]\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v_{r}(r,\unicode[STIX]{x1D703}) & = & \displaystyle -U\cos \unicode[STIX]{x1D703}+A_{0}\frac{a^{2}}{r^{2}}P_{0}+\frac{2}{3}(A_{1}+B_{1})\frac{a^{3}}{r^{3}}P_{1}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n=2}^{\infty }\left[\left(\frac{1}{2}n\frac{a^{n}}{r^{n}}-\left(\frac{1}{2}n-1\right)\frac{a^{n+2}}{r^{n+2}}\right)A_{n}P_{n}+\left(\frac{a^{n+2}}{r^{n+2}}-\frac{a^{n}}{r^{n}}\right)B_{n}P_{n}\right]\qquad\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle v_{\unicode[STIX]{x1D703}}(r,\unicode[STIX]{x1D703}) & = & \displaystyle U\sin \unicode[STIX]{x1D703}+\frac{1}{3}(A_{1}+B_{1})\frac{a^{3}}{r^{3}}V_{1}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n=2}^{\infty }\left[\left(\frac{1}{2}n\frac{a^{n+2}}{r^{n+2}}-\left(\frac{1}{2}n-1\right)\frac{a^{n}}{r^{n}}\right)B_{n}V_{n}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{1}{2}n\left(\frac{1}{2}n-1\right)\left(\frac{a^{n}}{r^{n}}-\frac{a^{n+2}}{r^{n+2}}\right)A_{n}V_{n}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v_{\unicode[STIX]{x1D703}}(r,\unicode[STIX]{x1D703}) & = & \displaystyle U\sin \unicode[STIX]{x1D703}+\frac{1}{3}(A_{1}+B_{1})\frac{a^{3}}{r^{3}}V_{1}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n=2}^{\infty }\left[\left(\frac{1}{2}n\frac{a^{n+2}}{r^{n+2}}-\left(\frac{1}{2}n-1\right)\frac{a^{n}}{r^{n}}\right)B_{n}V_{n}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{1}{2}n\left(\frac{1}{2}n-1\right)\left(\frac{a^{n}}{r^{n}}-\frac{a^{n+2}}{r^{n+2}}\right)A_{n}V_{n}\right],\end{eqnarray}$$
where
![]() $a$
is the squirming surface, i.e. the mean radius of the ciliary envelope,
$a$
is the squirming surface, i.e. the mean radius of the ciliary envelope,
![]() $U$
is the swimming speed of the squirmer,
$U$
is the swimming speed of the squirmer,
![]() $P_{n}$
is the Legendre polynomial and
$P_{n}$
is the Legendre polynomial and
The velocity on the surface of sphere
![]() $r=a$
is given by
$r=a$
is given by
The swimming velocity
![]() $U$
and the coefficients
$U$
and the coefficients
![]() $A_{1}$
and
$A_{1}$
and
![]() $B_{1}$
satisfy the following relation:
$B_{1}$
satisfy the following relation:
If the ciliary envelope is set outside the individual cilia, equation (4.5) should describe the swimming velocity of our present model. However, if the ciliary envelope overlaps with individual cilia, a propulsion force is generated even outside the envelope and (4.5) is no longer valid. We thus calculated the velocities
![]() $v_{r}$
and
$v_{r}$
and
![]() $v_{\unicode[STIX]{x1D703}}$
at
$v_{\unicode[STIX]{x1D703}}$
at
![]() $r=a_{0}+L+\unicode[STIX]{x1D716}$
, where
$r=a_{0}+L+\unicode[STIX]{x1D716}$
, where
![]() $a_{0}$
is the cell radius and
$a_{0}$
is the cell radius and
![]() $L$
is the length of a cilium. Here
$L$
is the length of a cilium. Here
![]() $\unicode[STIX]{x1D716}$
is an offset used to avoid the singularity and to increase the accuracy of numerical integration;
$\unicode[STIX]{x1D716}$
is an offset used to avoid the singularity and to increase the accuracy of numerical integration;
![]() $\unicode[STIX]{x1D716}/L$
was set to 0.1. We averaged
$\unicode[STIX]{x1D716}/L$
was set to 0.1. We averaged
![]() $v_{r}$
and
$v_{r}$
and
![]() $v_{\unicode[STIX]{x1D703}}$
in the circumferential direction, and estimated
$v_{\unicode[STIX]{x1D703}}$
in the circumferential direction, and estimated
![]() $A_{n}$
and
$A_{n}$
and
![]() $B_{n}$
of our present ciliate model using a least-squares method to fit the data to (4.4). We used 50 points in the
$B_{n}$
of our present ciliate model using a least-squares method to fit the data to (4.4). We used 50 points in the
![]() $\unicode[STIX]{x1D703}$
-direction to estimate
$\unicode[STIX]{x1D703}$
-direction to estimate
![]() $A_{1}$
and
$A_{1}$
and
![]() $B_{1}$
, and the swimming velocity was then calculated employing (4.5).
$B_{1}$
, and the swimming velocity was then calculated employing (4.5).
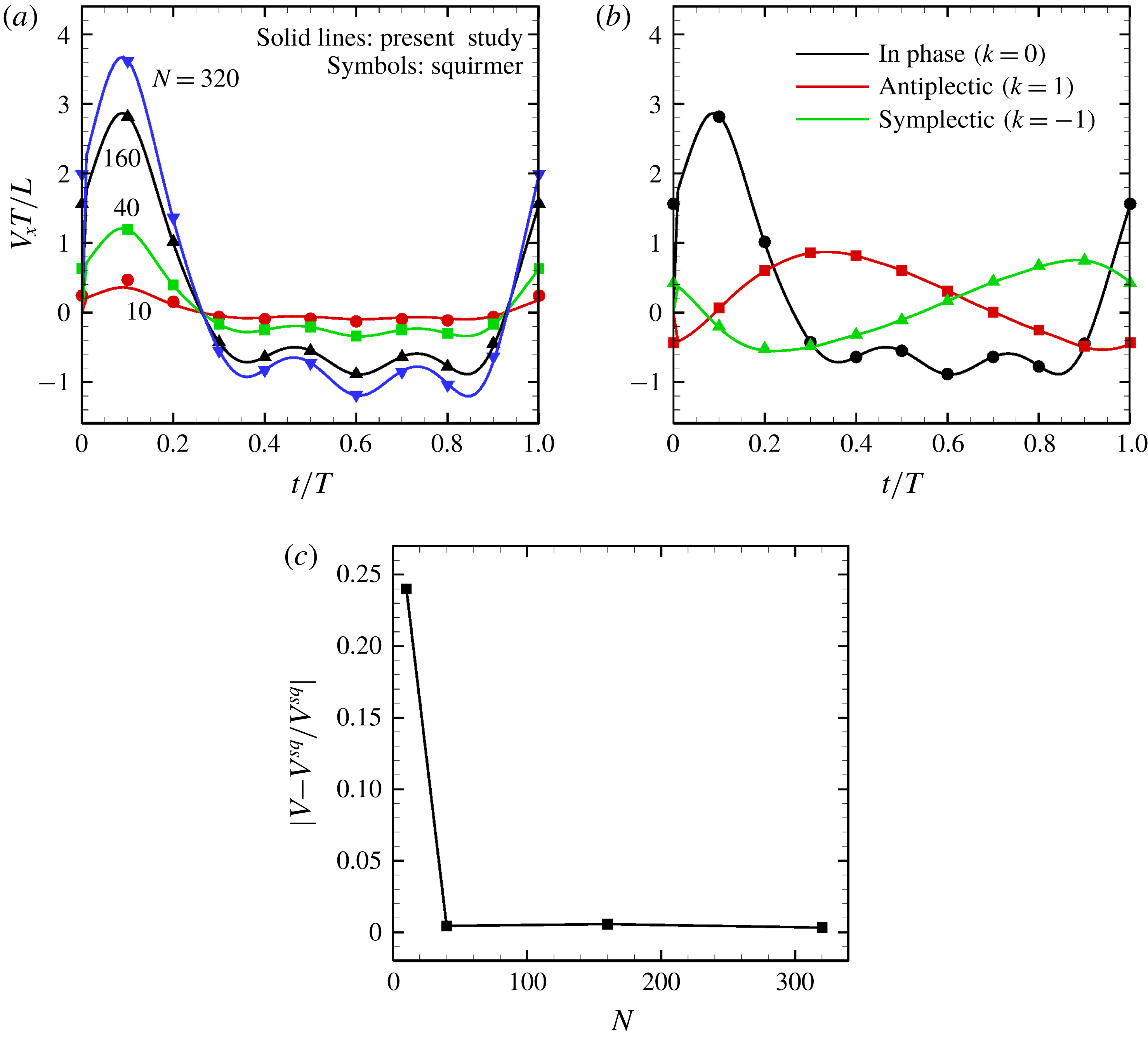
Figure 12. Comparison with the squirmer. Solid lines express present numerical results, whereas symbols are the theory (Blake Reference Blake1971). (a) Effect of the cilia number
![]() $N$
on the temporal swimming speed with in-phase wave. (b) Temporal swimming speed with antiplectic and symplectic waves
$N$
on the temporal swimming speed with in-phase wave. (b) Temporal swimming speed with antiplectic and symplectic waves
![]() $(N=160)$
. (c) Difference of maximum swimming speed between the present numerical results (in-phase beating) and the squirmer.
$(N=160)$
. (c) Difference of maximum swimming speed between the present numerical results (in-phase beating) and the squirmer.
The time changes in swimming velocities outlined in this study and squirmers with three different types of metachronism are shown in figure 12. In all cases, there is quantitative agreement between the two models. We also compared maximum swimming speeds between our numerical model and the squirmers. As shown in figure 12(c), we found quantitative agreement, and the difference between the two models was less than 1 % when
![]() $N>10$
. We thus confirmed that swimming velocity can be predicted by the Lighthill–Blake theory when the ciliary envelope is set outside the individual cilia.
$N>10$
. We thus confirmed that swimming velocity can be predicted by the Lighthill–Blake theory when the ciliary envelope is set outside the individual cilia.
4.2 Energy dissipation
In the squirmer model, the instantaneous rate of working of the stress at the squirming surface
![]() $a$
is given by
$a$
is given by
where
![]() $\unicode[STIX]{x1D748}$
is the viscous stress. In an isolated system, the above
$\unicode[STIX]{x1D748}$
is the viscous stress. In an isolated system, the above
![]() $P$
-value reflects the rate of viscous energy dissipation via fluid motion. In the squirmer model, fluid motion inside the ciliary envelope is not considered; thus, viscous energy dissipation is only considered outside the envelope. We calculated energy dissipation inside the ciliary envelope using our model.
$P$
-value reflects the rate of viscous energy dissipation via fluid motion. In the squirmer model, fluid motion inside the ciliary envelope is not considered; thus, viscous energy dissipation is only considered outside the envelope. We calculated energy dissipation inside the ciliary envelope using our model.
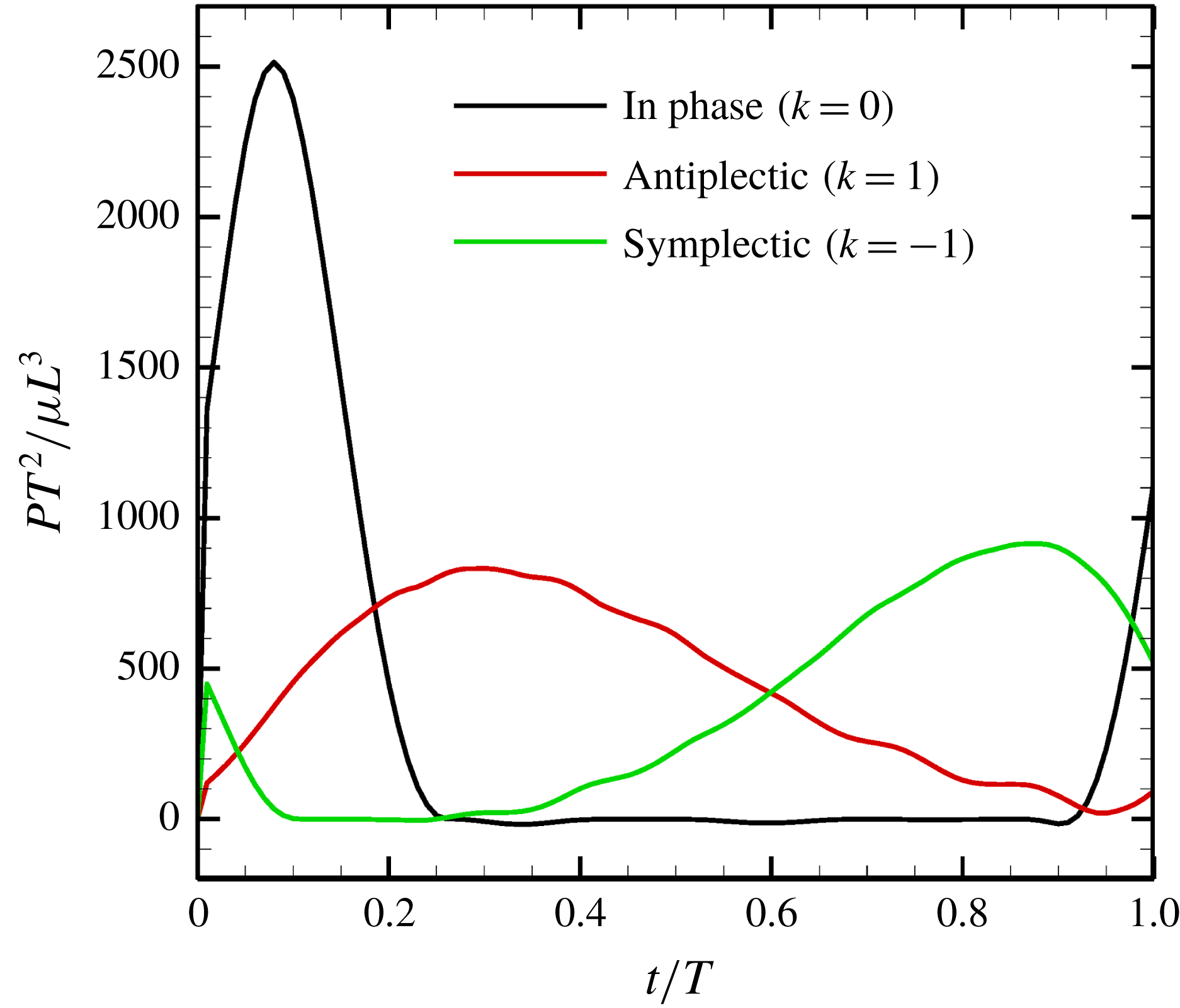
Figure 13. Power generated by ciliary beat with three different metachronal waves.
The powers associated with movement of the cell body and cilia are given by
and
The rate of energy dissipation occurring outside the envelope can be given by
where
![]() $a=a_{0}+L+\unicode[STIX]{x1D716}$
is the squirming surface. Considering the energy conservation, the rate of energy dissipation inside the envelope
$a=a_{0}+L+\unicode[STIX]{x1D716}$
is the squirming surface. Considering the energy conservation, the rate of energy dissipation inside the envelope
![]() $P_{in}$
is given by
$P_{in}$
is given by
To calculate the infinite integral (4.9), we split
![]() $P_{out}$
into two parts,
$P_{out}$
into two parts,
where
![]() $r_{c}$
is the domain truncation. As the stress
$r_{c}$
is the domain truncation. As the stress
![]() $\unicode[STIX]{x1D748}$
is proportional to
$\unicode[STIX]{x1D748}$
is proportional to
![]() $r^{-3}$
in the far field, the energy
$r^{-3}$
in the far field, the energy
![]() $\unicode[STIX]{x1D748}\,\boldsymbol{ : }\,\unicode[STIX]{x1D735}\boldsymbol{v}$
is proportional to
$\unicode[STIX]{x1D748}\,\boldsymbol{ : }\,\unicode[STIX]{x1D735}\boldsymbol{v}$
is proportional to
![]() $r^{-6}$
(which can be numerically confirmed (data not shown)). We then assumed that
$r^{-6}$
(which can be numerically confirmed (data not shown)). We then assumed that
![]() $\unicode[STIX]{x1D748}\,\boldsymbol{ : }\,\unicode[STIX]{x1D735}\boldsymbol{v}\propto r^{-6}$
applied in the far field. In (4.11)
$\unicode[STIX]{x1D748}\,\boldsymbol{ : }\,\unicode[STIX]{x1D735}\boldsymbol{v}\propto r^{-6}$
applied in the far field. In (4.11)
![]() $P_{out}^{far}$
was analytically calculated at
$P_{out}^{far}$
was analytically calculated at
![]() $r=r_{c}$
using numerical data. The domain truncation
$r=r_{c}$
using numerical data. The domain truncation
![]() $r_{c}$
was set to
$r_{c}$
was set to
![]() $r_{c}/L=10$
, which is sufficiently large to allow computation of the near-field contribution. In the near field,
$r_{c}/L=10$
, which is sufficiently large to allow computation of the near-field contribution. In the near field,
![]() $P_{out}^{near}$
in (4.11) was numerically calculated via Gaussian numerical integration. The details are given in our earlier work (Omori et al.
Reference Omori, Sugai, Imai and Ishikawa2017).
$P_{out}^{near}$
in (4.11) was numerically calculated via Gaussian numerical integration. The details are given in our earlier work (Omori et al.
Reference Omori, Sugai, Imai and Ishikawa2017).
We first computed the power of the ciliary beat over a cycle with three different metachronal waves (in-phase, antiplectic and symplectic), and the results are shown in figure 13. The power generated was highest when cilia were in-phase. However, due to the increased duration of the recovery stroke, the rate of working over the cycle was small. In the case of the antiplectic wave, on the other hand, the effective time was longer, but the peak decreased, as did the swimming velocity (cf. figure 9). In the antiplectic mode, the rate of working of each cilium was large during the effective stroke and the wave propagated to neighbouring cilia as in Blake (Reference Blake1972). Thus, the total period of effective power was longer than for in-phase beating.
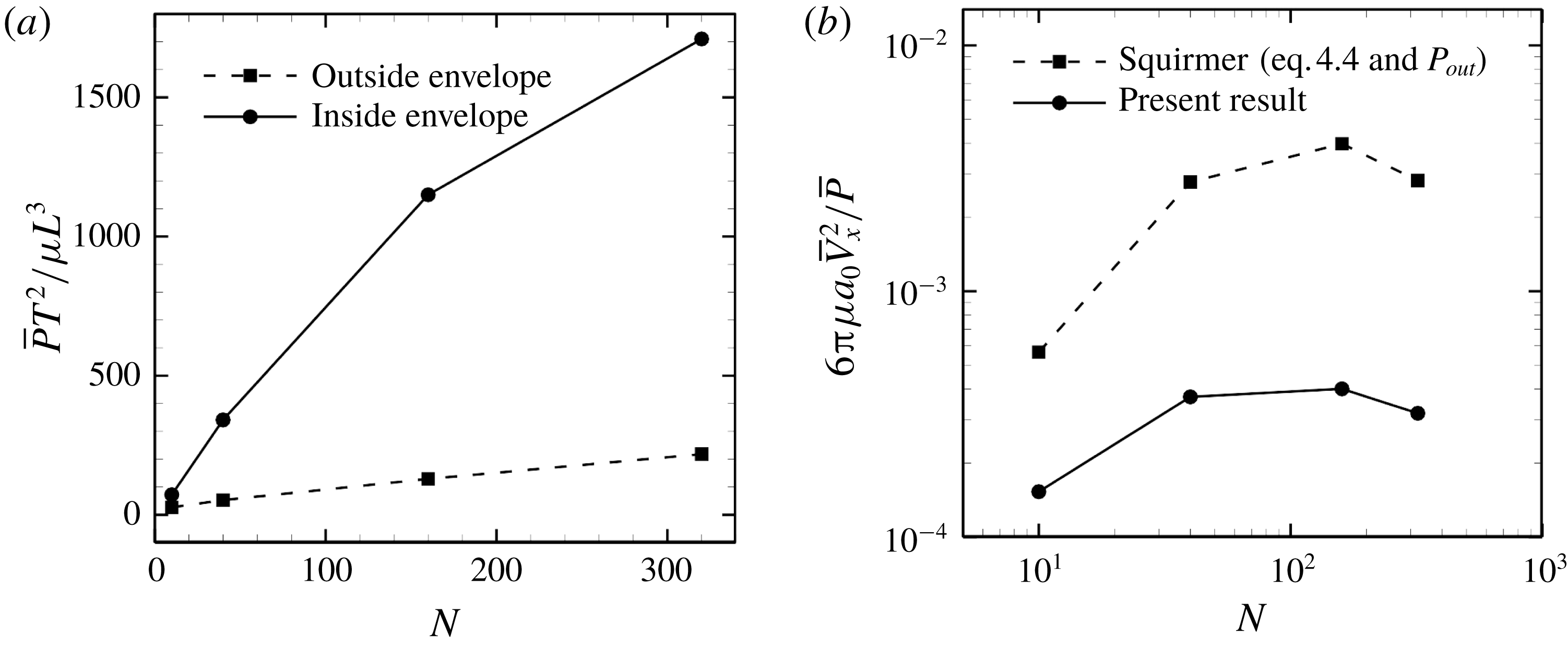
Figure 14. Effect of cilia number on the energy dissipation of a ciliate model. (a) Energy dissipations occurred outside and inside the ciliary envelope. (b) Efficiency of the swimming.
We then calculated energy dissipation occurring inside and outside the ciliary envelope, and results with in-phase beating are shown in figure 14(a). The energy loss inside the envelope,
![]() $P_{in}$
, rapidly increases with
$P_{in}$
, rapidly increases with
![]() $N$
, and approximately 90 % of the energy is dissipated within the envelope when
$N$
, and approximately 90 % of the energy is dissipated within the envelope when
![]() $N=320$
. Thus, most energy dissipation occurs within the envelope; ciliary motion, rather than fluid motion outside the envelope, explains most of the dissipation. Keller & Wu (Reference Keller and Wu1977) estimated energy dissipation inside the ciliary envelope analytically and found that over 95 % of dissipation occurred inside the envelope. They assumed that each cilium worked at the same rate and did not consider hydrodynamic interactions among cilia, unlike the current study. If we neglect hydrodynamic interactions, the total power due to ciliary beating should be proportional to the number of cilia. To clarify the effects of hydrodynamic interactions, we additionally calculated the power of a single cilium located on a flat plane; the result of this assessment was
$N=320$
. Thus, most energy dissipation occurs within the envelope; ciliary motion, rather than fluid motion outside the envelope, explains most of the dissipation. Keller & Wu (Reference Keller and Wu1977) estimated energy dissipation inside the ciliary envelope analytically and found that over 95 % of dissipation occurred inside the envelope. They assumed that each cilium worked at the same rate and did not consider hydrodynamic interactions among cilia, unlike the current study. If we neglect hydrodynamic interactions, the total power due to ciliary beating should be proportional to the number of cilia. To clarify the effects of hydrodynamic interactions, we additionally calculated the power of a single cilium located on a flat plane; the result of this assessment was
![]() $\bar{P}_{single}T^{2}/\unicode[STIX]{x1D707}L^{3}=9.74$
. Multiplying by
$\bar{P}_{single}T^{2}/\unicode[STIX]{x1D707}L^{3}=9.74$
. Multiplying by
![]() $N=320$
, we have
$N=320$
, we have
![]() $N\bar{P}_{single}T^{2}/\unicode[STIX]{x1D707}L^{3}=3116.8$
. This value is approximately twice as large as the numerical result in figure 14(a). This implies that hydrodynamic interactions within ciliary layers diminish the rate of working. Although the magnitude of ciliary power differed, the ratio of energy dissipation inside the envelope was almost the same in the present study as in the study by Keller & Wu (Reference Keller and Wu1977). This may be because both swimming velocity and energy dissipation outside the envelope decrease as a reflection of the reduced power of individual cilia.
$N\bar{P}_{single}T^{2}/\unicode[STIX]{x1D707}L^{3}=3116.8$
. This value is approximately twice as large as the numerical result in figure 14(a). This implies that hydrodynamic interactions within ciliary layers diminish the rate of working. Although the magnitude of ciliary power differed, the ratio of energy dissipation inside the envelope was almost the same in the present study as in the study by Keller & Wu (Reference Keller and Wu1977). This may be because both swimming velocity and energy dissipation outside the envelope decrease as a reflection of the reduced power of individual cilia.
When the energy dissipation is known, it is possible to calculate swimming efficiency. Swimming efficiency is defined as the time-average swimming speed and the power, e.g.
![]() $6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}a_{0}\bar{V}^{2}/\bar{P}$
for a spherical ciliate. In the case of in-phase beating, the efficiency of the ciliate model is 10-fold lower than that of the squirmer model, as shown in figure 14(b).
$6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}a_{0}\bar{V}^{2}/\bar{P}$
for a spherical ciliate. In the case of in-phase beating, the efficiency of the ciliate model is 10-fold lower than that of the squirmer model, as shown in figure 14(b).
We then investigated the effect of the aspect ratio on efficiency. As stated in former studies (Pironneau Reference Pironneau1973; Vilfan Reference Vilfan2012), the optimal profile for minimum dissipation is a prolate rather than an oblate ellipsoid, and the drag coefficient of a rigid spheroid is minimised when
![]() $\unicode[STIX]{x1D6FC}_{v}\sim 2$
(cf. figure 7
b). Swimming efficiency, on the other hand, has a different tendency due to the effect of the metachronal wave, as shown in figure 15. The efficiency of a symplectic wave increases with the aspect ratio, whereas an antiplectic wave is maximal at
$\unicode[STIX]{x1D6FC}_{v}\sim 2$
(cf. figure 7
b). Swimming efficiency, on the other hand, has a different tendency due to the effect of the metachronal wave, as shown in figure 15. The efficiency of a symplectic wave increases with the aspect ratio, whereas an antiplectic wave is maximal at
![]() $\unicode[STIX]{x1D6FC}_{v}\sim 1$
.
$\unicode[STIX]{x1D6FC}_{v}\sim 1$
.
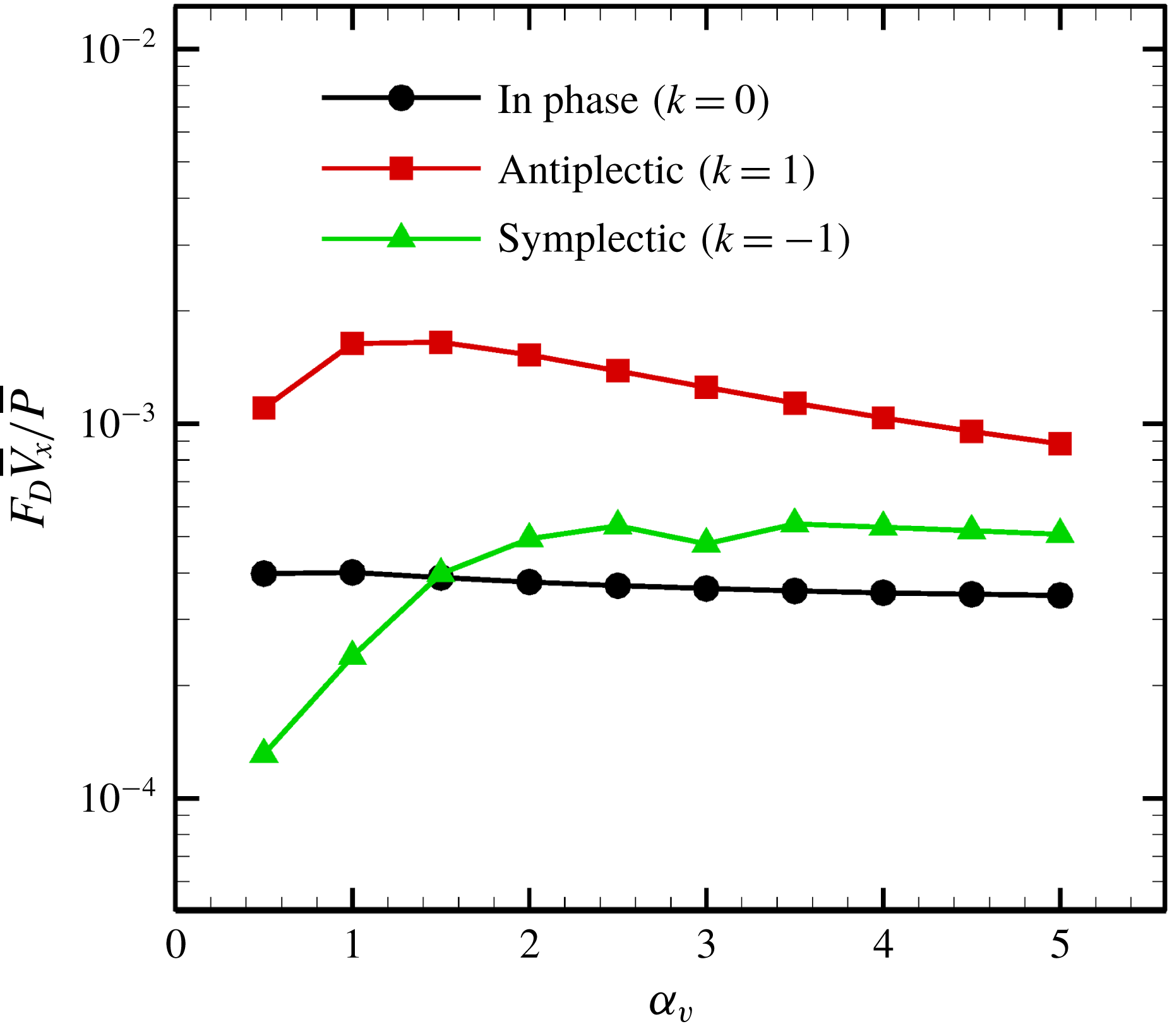
Figure 15. Swimming efficiency with various aspect ratios
![]() $\unicode[STIX]{x1D6FC}_{v}$
(
$\unicode[STIX]{x1D6FC}_{v}$
(
![]() $N=160$
).
$N=160$
).
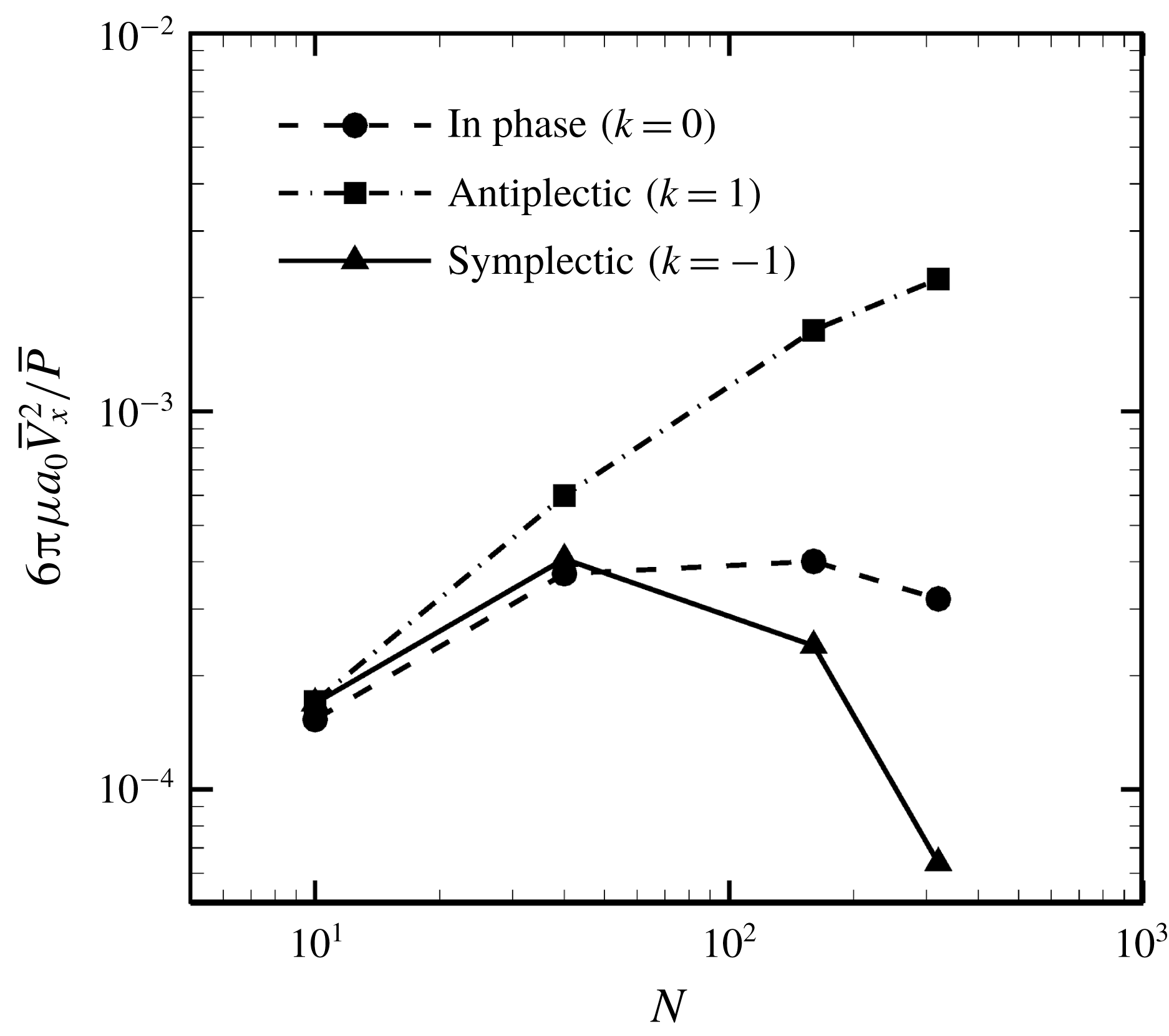
Figure 16. Effect of metachronal wave on the efficiency.
Finally, we investigated the effect of a metachronal wave on swimming efficiency. The ciliate shape was again set to a sphere with radius
![]() $a_{0}/L=3.0$
, and the result is shown in figure 16. The optimal efficiency was given by the antiplectic wave, and the value monotonically increased with the number of cilia. The efficiency of the antiplectic wave was approximately 6.7 times larger than that of the in-phase wave when
$a_{0}/L=3.0$
, and the result is shown in figure 16. The optimal efficiency was given by the antiplectic wave, and the value monotonically increased with the number of cilia. The efficiency of the antiplectic wave was approximately 6.7 times larger than that of the in-phase wave when
![]() $N=320$
. Several studies (Blake Reference Blake1972; Michelin & Lauga Reference Michelin and Lauga2010; Osterman & Vilfan Reference Osterman and Vilfan2011) also found that an antiplectic metachronal wave resulted in optimal efficiency. Thus, we confirmed qualitative agreement between the present and former studies. We also found that the ratio of energy dissipation inside and outside of the ciliary envelope was not significantly modified by the ciliary beat configuration. Hence, the antiplectic wave becomes the most efficient not only by considering the dissipation outside the envelope but also by considering both inside and outside dissipations.
$N=320$
. Several studies (Blake Reference Blake1972; Michelin & Lauga Reference Michelin and Lauga2010; Osterman & Vilfan Reference Osterman and Vilfan2011) also found that an antiplectic metachronal wave resulted in optimal efficiency. Thus, we confirmed qualitative agreement between the present and former studies. We also found that the ratio of energy dissipation inside and outside of the ciliary envelope was not significantly modified by the ciliary beat configuration. Hence, the antiplectic wave becomes the most efficient not only by considering the dissipation outside the envelope but also by considering both inside and outside dissipations.
Blake (Reference Blake1974) investigated the optimal spacing of cilia for efficiency and found efficiency to be maximum at
![]() $\unicode[STIX]{x0394}x/L=0.25$
for antiplectic waves, where
$\unicode[STIX]{x0394}x/L=0.25$
for antiplectic waves, where
![]() $\unicode[STIX]{x0394}x$
is the spacing. In our simulations, swimming efficiency increased monotonically with
$\unicode[STIX]{x0394}x$
is the spacing. In our simulations, swimming efficiency increased monotonically with
![]() $N$
when cilia were beating in antiplectic mode (cf. figure 16), and the minimum spacing was
$N$
when cilia were beating in antiplectic mode (cf. figure 16), and the minimum spacing was
![]() $\unicode[STIX]{x0394}x/L=0.59$
with
$\unicode[STIX]{x0394}x/L=0.59$
with
![]() $N=320$
. This value is approximately 2.3 times larger than Blake’s estimation. Osterman & Vilfan (Reference Osterman and Vilfan2011) numerically calculated ciliary beating efficiency by considering the losses inside the ciliary layer, and reported that the maximum efficiency was given by an antiplectic wave with an inter-ciliary distance
$N=320$
. This value is approximately 2.3 times larger than Blake’s estimation. Osterman & Vilfan (Reference Osterman and Vilfan2011) numerically calculated ciliary beating efficiency by considering the losses inside the ciliary layer, and reported that the maximum efficiency was given by an antiplectic wave with an inter-ciliary distance
![]() $\unicode[STIX]{x0394}x\sim 0.25L$
. The resulting optimal swimming efficiency was 0.016, which is approximately 10 times larger than our numerical result of the antiplectic wave with
$\unicode[STIX]{x0394}x\sim 0.25L$
. The resulting optimal swimming efficiency was 0.016, which is approximately 10 times larger than our numerical result of the antiplectic wave with
![]() $N=320$
(cf. figure 16). The discrepancy may arise from the difference in the number of cilia between the two studies: at most 320 cilia were used in the present study, whereas an infinite number of cilia with periodic boundary was set in Osterman & Vilfan (Reference Osterman and Vilfan2011). Since the efficiency of an antiplectic wave monotonically increases with the number of cilia in the present study, the difference may be reduced by further increasing
$N=320$
(cf. figure 16). The discrepancy may arise from the difference in the number of cilia between the two studies: at most 320 cilia were used in the present study, whereas an infinite number of cilia with periodic boundary was set in Osterman & Vilfan (Reference Osterman and Vilfan2011). Since the efficiency of an antiplectic wave monotonically increases with the number of cilia in the present study, the difference may be reduced by further increasing
![]() $N$
. Another possibility for the discrepancy is the difference in the ciliary beat pattern between the two studies. The amplitude of the ciliary beat in Osterman & Vilfan (Reference Osterman and Vilfan2011) is larger than ours, which may make their efficiency larger. We could not employ the same beat pattern in this study, because the cilia tend to collide frequently with each other, and non-hydrodynamic forces start to play a role.
$N$
. Another possibility for the discrepancy is the difference in the ciliary beat pattern between the two studies. The amplitude of the ciliary beat in Osterman & Vilfan (Reference Osterman and Vilfan2011) is larger than ours, which may make their efficiency larger. We could not employ the same beat pattern in this study, because the cilia tend to collide frequently with each other, and non-hydrodynamic forces start to play a role.
Katsu-Kimura et al. (Reference Katsu-Kimura, Nakaya, Baba and Mogami2009) also experimentally estimated the energetic efficiency of swimming in Paramecium as 0.078 %, which includes losses in metabolism. This value is still above the results of the present study. We think the ciliary configurations used in this study, such as number and density of cilia, and ciliary beat pattern, caused the quantitative difference from the experimental result of Katsu-Kimura et al. (Reference Katsu-Kimura, Nakaya, Baba and Mogami2009). We would like to address these effects in our future studies by overcoming numerical difficulties caused by the collision of cilia.
5 Conclusions
We developed a ciliate model using the slender-body–boundary integral coupling method. We found that an antiplectic metachronal wave of wavenumber
![]() $k=1.0$
optimised the swimming speed when the cellular body assumed various aspect ratios. We used oblique wave propagation to reproduce the helical swimming trajectories of even spherical ciliates exerting axisymmetric, time-averaged ciliary forces. We also compared our numerical model to the squirmer model of Lighthill and Blake. The swimming speed afforded by our discrete ciliary model agreed with that derived using Lighthill–Blake theory. However, the squirmer model considers only events outside the ciliary envelope, and thus fails to accurately estimate the energy cost of swimming; over 90 % of the energy was dissipated inside the ciliary envelope. The results of this study show that swimming efficiency was optimal with an antiplectic wave, which is consistent with former studies. The efficiency was 6.7 times larger than that of in-phase beating when the number of cilia was
$k=1.0$
optimised the swimming speed when the cellular body assumed various aspect ratios. We used oblique wave propagation to reproduce the helical swimming trajectories of even spherical ciliates exerting axisymmetric, time-averaged ciliary forces. We also compared our numerical model to the squirmer model of Lighthill and Blake. The swimming speed afforded by our discrete ciliary model agreed with that derived using Lighthill–Blake theory. However, the squirmer model considers only events outside the ciliary envelope, and thus fails to accurately estimate the energy cost of swimming; over 90 % of the energy was dissipated inside the ciliary envelope. The results of this study show that swimming efficiency was optimal with an antiplectic wave, which is consistent with former studies. The efficiency was 6.7 times larger than that of in-phase beating when the number of cilia was
![]() $N=320$
. Our findings provide a fundamental basis for modelling swimming micro-organisms.
$N=320$
. Our findings provide a fundamental basis for modelling swimming micro-organisms.
Acknowledgement
This research was supported by JSPS KAKENHI grants, numbers 17H00853 and 18K18354.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2019.490.
Appendix A. Validation of the numerical method
In this appendix, we explain the accuracy of our numerical method. We validated the numerical method by calculating the viscous drag of a rigid sphere or a slender ellipsoid. We first calculated the drag of a sphere in a uniform flow by using a boundary element method. We compared the numerical results with the analytical solution of Stokes’ law,
![]() $6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}aU$
, where
$6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}aU$
, where
![]() $U$
is the velocity,
$U$
is the velocity,
![]() $\unicode[STIX]{x1D707}$
is the viscosity and
$\unicode[STIX]{x1D707}$
is the viscosity and
![]() $a$
is the radius of the sphere. We confirmed that the error became less than 0.1 % when we used 5120 triangular elements or larger meshes. We then calculated the drag of a slender ellipsoid in a uniform flow. We set two different flow directions, as shown in figure 17(a), and compared the results using slender-body theory and the boundary element method. To estimate numerical accuracy, we defined the force difference between the slender-body theory (SBT) and the boundary element method (BEM) as
$a$
is the radius of the sphere. We confirmed that the error became less than 0.1 % when we used 5120 triangular elements or larger meshes. We then calculated the drag of a slender ellipsoid in a uniform flow. We set two different flow directions, as shown in figure 17(a), and compared the results using slender-body theory and the boundary element method. To estimate numerical accuracy, we defined the force difference between the slender-body theory (SBT) and the boundary element method (BEM) as
The results are shown in figure 17(b). The force differences are less than 1 % when the slenderness
![]() $\unicode[STIX]{x1D700}=r/L$
is smaller than
$\unicode[STIX]{x1D700}=r/L$
is smaller than
![]() $10^{-2}$
in both the normal and tangential directions (
$10^{-2}$
in both the normal and tangential directions (
![]() $\unicode[STIX]{x0394}F_{n}$
and
$\unicode[STIX]{x0394}F_{n}$
and
![]() $\unicode[STIX]{x0394}F_{t}$
), where
$\unicode[STIX]{x0394}F_{t}$
), where
![]() $r$
is the semi-minor axis and
$r$
is the semi-minor axis and
![]() $L$
is the length. In the case of a cilium, a typical length is
$L$
is the length. In the case of a cilium, a typical length is
![]() $10~\unicode[STIX]{x03BC}\text{m}$
and a typical radius is 100 nm; thus
$10~\unicode[STIX]{x03BC}\text{m}$
and a typical radius is 100 nm; thus
![]() $\unicode[STIX]{x1D700}$
can be estimated as
$\unicode[STIX]{x1D700}$
can be estimated as
![]() $10^{-2}$
. This confirms that our numerical method has sufficient accuracy to simulate the swimming of ciliates.
$10^{-2}$
. This confirms that our numerical method has sufficient accuracy to simulate the swimming of ciliates.
Figure 17. Comparison with a slender-body theory (SBT) and a boundary element method (BEM). (a) Uniform flow around a slender body with
![]() $\unicode[STIX]{x1D700}=10^{-2}$
. We set two different flow directions. (b) Force difference between the slender-body theory and the boundary element method.
$\unicode[STIX]{x1D700}=10^{-2}$
. We set two different flow directions. (b) Force difference between the slender-body theory and the boundary element method.





















