Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-25T05:52:41.964Z Has data issue: false hasContentIssue false
  • English
  • Français

Surface-tension- and injection-driven spreading of a thin viscous film

Published online by Cambridge University Press:  28 December 2018

K. B. Kiradjiev Open the ORCID record for K. B. Kiradjiev [Opens in a new window] ,
C. J. W. Breward Open the ORCID record for C. J. W. Breward [Opens in a new window]  and
I. M. Griffiths Open the ORCID record for I. M. Griffiths [Opens in a new window]
K. B. Kiradjiev*
Affiliation:
Mathematical Institute, University of Oxford, Radcliffe Observatory Quarter, Woodstock Rd, Oxford OX2 6GG, UK
C. J. W. Breward
Affiliation:
Mathematical Institute, University of Oxford, Radcliffe Observatory Quarter, Woodstock Rd, Oxford OX2 6GG, UK
I. M. Griffiths
Affiliation:
Mathematical Institute, University of Oxford, Radcliffe Observatory Quarter, Woodstock Rd, Oxford OX2 6GG, UK
*
†Email address for correspondence: kristian.kiradjiev@maths.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the spreading of a thin viscous droplet, injected through a finite region of a substrate, under the influence of surface tension. We neglect gravity and assume that there is a precursor layer covering the whole substrate and that the rate of injection is constant. We analyse the evolution of the film profile for early and late time, and obtain power-law dependencies for the maximum film thickness at the centre of the injection region and the position of an apparent contact line, which compare well with numerical solutions of the full problem. We relax the conditions on the injection rate to consider more general time-dependent and spatially varying forms. In the case of power-law injection of the form $t^{k}$, we observe a switch in the behaviour of the evolution of the film thickness for late time from increasing to decreasing at a critical value of 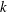$k$. We show that point-source injection can be treated as a limiting case of a finite-injection slot and the solutions exhibit identical behaviours for late time. Finally, we formulate the problem with thickness-dependent injection rate, discuss the behaviour of the maximum film thickness and the position of the apparent contact line and give power-law dependencies for these.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Low-Reynolds-number flows: Low-Reynolds-number flows Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 861 , 25 February 2019 , pp. 765 - 795
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ajaev, V. S. 2012 Interfacial Fluid Mechanics: A Mathematical Modelling Approach. Springer.Google Scholar
Anderson, D. M. & Davis, H. 1995 The spreading of volatile liquid droplets on heated surfaces. Phys. Fluids 7 (2), 248–265.Google Scholar
Benilov, E. S., Chapman, S. J., McLeod, J. B., Ockendon, J. R. & Zubkov, V. S. 2010 On liquid films on an inclined plate. J. Fluid Mech. 663, 53–69.Google Scholar
Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolley, E. 2009 Wetting and spreading. Rev. Mod. Phys. 81 (2), 739–805.Google Scholar
Carlson, A., Mandre, S. & Mahadevan, L.2015 Elastohydrodynamics of contact in adherent sheets. Preprint, 2015, arXiv:1508.06234.Google Scholar
Chilukuri, R., Aeling, D. & Middleman, S. 1984 Removal of a thin liquid film from a flat surface using an axisymmetric impinging jet. J. Fluids Engng 106 (2), 223–226.Google Scholar
Cox, R. G. 1986 The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech. 168, 169–194.Google Scholar
Craster, R. V. & Matar, O. K. 2009 Dynamics and stability of thin liquid films. Rev. Mod. Phys. 81, 1131–1198.Google Scholar
Davis, S. H. & Hocking, L. M. 1999 Spreading and imbibition of viscous liquid on a porous base. Phys. Fluids 11 (1), 48–57.Google Scholar
Davis, S. H. & Hocking, L. M. 2000 Spreading and imbibition of viscous liquid on a porous base. II. Phys. Fluids 12 (7), 1646–1655.Google Scholar
Diez, J. A., Kondic, L. & Bertozzi, A. 2001 Global models for moving contact lines. Phys. Rev. E 63, 1–13.Google Scholar
Duffy, B. R. & Moffatt, H. K. 1997 A similarity solution for viscous source flow on a vertical plane. Eur. J. Appl. Maths 8, 37–47.Google Scholar
Duffy, B. R. & Wilson, S. K. 1997 A third-order differential equation arising in thin-film flows and relevant to tanner’s law. Appl. Math. Lett. 10 (3), 63–68.Google Scholar
Ehrhard, P. & Davis, S. H. 1991 Non-isothermal spreading of liquid drops on horizontal plates. J. Fluid Mech. 229, 365–388.Google Scholar
Fraysse, N. & Homsy, G. M. 1994 An experimental study of rivulet instabilities in centrifugal spin coating of viscous Newtonian and non-Newtonian fluids. Phys. Fluids 6 (4), 1491–1504.Google Scholar
Guzman, R. & Vasquez, D. A. 2016 Surface tension driven flow on a thin reaction front. Eur. Phys. J. Spec. Top. 225 (13–14), 2573–2580.Google Scholar
Halpern, D. & Grotberg, J. B. 1992 Fluid–elastic instabilities of liquid-lined flexible tubes. J. Fluid Mech. 244, 615–632.Google Scholar
Hocking, G. C., Sweatman, W. L., Fitt, A. D. & Breward, C. 2011 Deformations during jet-stripping in the galvanizing process. J. Engng Maths 70 (1–3), 297–306.Google Scholar
Hocking, L. M. 1980 Sliding and spreading of two-dimensional drops. Q. J. Mech. Appl. Maths 34 (1), 37–55.Google Scholar
Hocking, L. M. 1983 The spreading of a thin drop by gravity and capillarity. Q. J. Mech. Appl. Maths 36 (1), 55–69.Google Scholar
Hocking, L. M. 1992 Rival contact-angle models and the spreading of drops. J. Fluid Mech. 239, 671–681.Google Scholar
Howell, P. D. 2010 Surface-tension-driven flow on a moving curved surface. J. Engng Maths 45 (3), 283–308.Google Scholar
Howell, P. D., Robinson, J. & Stone, H. A. 2013 Gravity-driven thin-film flow on a flexible substrate. J. Fluid Mech. 732, 190–213.Google Scholar
Howison, S. D., Moriarty, J. A., Ockendon, J. R., Terrill, E. L. & Wilson, S. K. 1997 A mathematical model for drying paint layers. J. Engng Maths 32 (4), 377–394.Google Scholar
Huh, C. & Scriven, L. E. 1971 Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 35 (1), 85–101.Google Scholar
Huppert, H. E. 1982 The propagation of two-dimensional and axisymmetric viscous gravity currents over a rigid horizontal surface. J. Fluid Mech. 121, 43–58.Google Scholar
King, J. R. & Bowen, M. 2001 Moving boundary problems and non-uniqueness for the thin film equation. Eur. J. Appl. Maths 12 (3), 321–356.Google Scholar
Lacey, A. A. 1982 The motion with slip of a thin viscous droplet over a solid surface. Stud. Appl. Maths 67 (3), 217–230.Google Scholar
Lister, J. R. 1992 Viscous flows down an inclined pane from point and line sources. J. Fluid Mech. 242, 631–653.Google Scholar
Lister, J. R., Peng, G. G. & Neufeld, J. A. 2013 Viscous control of peeling an elastic sheet by bending and pulling. Phys. Rev. Lett. 111 (15), 1–5.Google Scholar
Mason, D. P. & Momoniat, E. 2004 Axisymmetric spreading of a thin liquid drop with suction or blowing at the horizontal base. Intl J. Non-Linear Mech. 39, 1013–1026.Google Scholar
McEwan, A. D. & Taylor, G. I. 1966 The peeling of a flexible strip attached by a viscous adhesive. J. Fluid Mech. 26 (1), 1–15.Google Scholar
McKinley, I. S., Wilson, S. K. & Duffy, B. R. 1999 Spin coating and air-jet blowing of thin viscous drops. Phys. Fluids 11 (1), 30–47.Google Scholar
Momoniat, E. & Mason, D. P. 2007 Spreading of a thin film with suction or blowing including surface tension effects. Intl J. Comput. Maths Appl. 53 (2), 198–208.Google Scholar
Momoniat, E., Ravindran, R. & Roy, S. 2010 The influence of slot injection/suction on the spreading of a thin film under gravity and surface tension. Acta Mech. 211 (1–2), 61–71.Google Scholar
Murphy, E. A. & Lee, W. T. 2017 Mathematical modelling of contact lens moulding. IMA J. Appl. Maths 82 (3), 473–495.Google Scholar
Myers, T. G. 1998 Thin films with high surface tension. SIAM Rev. 40 (3), 441–462.Google Scholar
Oliver, J. M., Whiteley, J. P., Saxton, M. A., Vella, D., Zubkov, V. S. & King, J. R. 2015 On contact-line dynamics with mass transfer. Eur. J. Appl. Maths 26 (5), 671–719.Google Scholar
Oron, A., Davis, S. H. & Bankoff, S. G. 1997 Long-scale evolution of thin liquid films. Rev. Mod. Phys. 69 (3), 931–980.Google Scholar
Savva, N. & Kalliadasis, S. 2009 Two-dimensional droplet spreading over topographical substrates. Phys. Fluids 21 (9), 92102.Google Scholar
Savva, N. & Kalliadasis, S. 2011 Dynamics of moving contact lines: a comparison between slip and precursor film models. Europhys. Lett. 94 (6), 64004.Google Scholar
Savva, N. & Kalliadasis, S. 2013 Droplet motion on inclined heterogeneous substrates. J. Fluid Mech. 725, 462–491.Google Scholar
Saxton, M. A., Vella, D., Whiteley, J. P. & Oliver, J. M. 2017 Kinetic effects regularize the mass-flux singularity at the contact line of a thin evaporating drop. J. Engng Maths 106 (1), 47–73.Google Scholar
Saxton, M. A., Whiteley, J. P., Vella, D. & Oliver, J. M. 2016 On thin evaporating drops: when is the d2-law valid? J. Fluid Mech. 792, 134–167.Google Scholar
Schwartz, L. W. & Michaelides, L. E. 1988 Gravity flow of a viscous liquid down a slope with injection. Phys. Fluids 31 (1988), 397–399.Google Scholar
Sibley, D. N., Nold, A., Savva, N. & Kalliadasis, S. 2015 A comparison of slip, disjoining pressure, and interface formation models for contact line motion through asymptotic analysis of thin two-dimensional droplet spreading. J. Engng Maths 94 (1), 19–41.Google Scholar
Smith, P. C. 1973 A similarity solution for slow viscous flow down an inclined plane. J. Fluid Mech. 58 (2), 275–288.Google Scholar
Tanner, L. H. 1979 The spreading of silicone oil drops on horizontal surfaces. J. Phys. D 12, 1473–1484.Google Scholar
Thompson, A. B., Tseluiko, D. & Papageorgiou, D. T. 2015 Falling liquid films with blowing and suction. J. Fluid Mech. 787, 292–330.Google Scholar
Tuck, E. O. & Schwartz, L. W. 1990 A numerical and asymptotic study of some third-order ordinary differential equations relevant to draining and coating flows. SIAM Rev. 32 (3), 453–469.Google Scholar
Voinov, O. V. 1976 Hydrodynamics of wetting. Fluid Dyn. 11 (5), 714–721.Google Scholar
Wilson, S. D. R. 1982 The drag-out problem in film coating theory. J. Engng Maths 16 (3), 209–221.Google Scholar
Wilson, S. K., Hunt, R. & Duffy, B. R. 2000 The rate of spreading in spin coating. J. Fluid Mech. 413, 65–88.Google Scholar
Yatim, Y. M., Duffy, B. R. & Wilson, S. K. 2012 Similarity solutions for unsteady shear-stress-driven flow of Newtonian and power-law fluids: slender rivulets and dry patches. J. Engng Maths 73 (1), 53–69.Google Scholar
Yatim, Y. M., Duffy, B. R. & Wilson, S. K. 2013 Travelling-wave similarity solutions for a steadily translating slender dry patch in a thin fluid film. Phys. Fluids 25 (5), 52103.Google Scholar
Yatim, Y. M., Wilson, S. K. & Duffy, B. R. 2010 Unsteady gravity-driven slender rivulets of a power-law fluid. J. Non-Newtonian Fluid Mech. 165 (21–22), 1423–1430.Google Scholar
Zheng, Z., Fontelos, M. A., Shin, S., Dallaston, M. C., Tseluiko, D., Kalliadasis, S. & Stone, H. A. 2018 Healing capillary films. J. Fluid Mech. 838, 404–434.Google Scholar
Zheng, Z., Griffiths, I. M. & Stone, H. A. 2015 Propagation of a viscous thin film over an elastic membrane. J. Fluid Mech. 784, 443–464.Google Scholar