Article contents
Streaky dynamo equilibria persisting at infinite Reynolds numbers
Published online by Cambridge University Press: 17 December 2019
Abstract
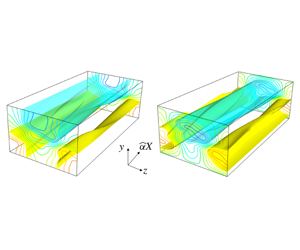
Nonlinear three-dimensional dynamo equilibrium solutions of viscous-resistive magneto-hydrodynamic equations are continued to formally infinite magnetic and hydrodynamic Reynolds numbers. The external driving mechanism of the dynamo is a uniform shear, which constitutes the base laminar flow and cannot support any kinematic dynamo. Nevertheless, an efficient subcritical nonlinear instability mechanism is found to be able to generate large-scale coherent structures known as streaks, for both velocity and magnetic fields. A finite amount of magnetic field generation is identified at the self-consistent asymptotic limit of the nonlinear solutions, thereby confirming the existence of an effective nonlinear dynamo action at astronomically large Reynolds numbers.
- Type
- JFM Rapids
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 1
- Cited by


