Article contents
Steady free surface flows induced by a submerged ring source or sink
Published online by Cambridge University Press: 24 January 2012
Abstract
The steady axisymmetric flow induced by a ring sink (or source) submerged in an unbounded inviscid fluid is computed and the resulting deformation of the free surface is obtained. Solutions are obtained analytically in the limit of small Froude number (and hence small surface deformation) and numerically for the full nonlinear problem. The small Froude number solutions are found to have the property that if the non-dimensional radius of the ring sink is less than 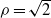 , there is a central stagnation point on the surface surrounded by a dip which rises to the stagnation level in the far distance. However, as the radius of the ring sink increases beyond
, there is a central stagnation point on the surface surrounded by a dip which rises to the stagnation level in the far distance. However, as the radius of the ring sink increases beyond  , a surface stagnation ring forms and moves outward as the ring sink radius increases. It is also shown that as the radius of the sink increases, the solutions in the vicinity of the ring sink/source change continuously from those due to a point sink/source (
, a surface stagnation ring forms and moves outward as the ring sink radius increases. It is also shown that as the radius of the sink increases, the solutions in the vicinity of the ring sink/source change continuously from those due to a point sink/source ( ) to those due to a line sink/source (
) to those due to a line sink/source (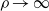 ). These properties are confirmed by the numerical solutions to the full nonlinear equations for finite Froude numbers. At small values of the Froude number and sink or source radius, the nonlinear solutions look like the approximate solutions, but as the flow rate increases a limiting maximum Froude number solution with a secondary stagnation ring is obtained. At large values of sink or source radius, however, this ring does not form and there is no obvious physical reason for the limit on solutions. The maximum Froude numbers at which steady solutions exist for each radius are computed.
). These properties are confirmed by the numerical solutions to the full nonlinear equations for finite Froude numbers. At small values of the Froude number and sink or source radius, the nonlinear solutions look like the approximate solutions, but as the flow rate increases a limiting maximum Froude number solution with a secondary stagnation ring is obtained. At large values of sink or source radius, however, this ring does not form and there is no obvious physical reason for the limit on solutions. The maximum Froude numbers at which steady solutions exist for each radius are computed.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 5
- Cited by


