1. Introduction
The study of passive tracer transport is of fundamental importance in characterizing turbulence. However, predicting a chaotic dynamical trajectory over long times is infeasible (Lorenz Reference Lorenz1963), so one must switch to a statistical perspective to make headway on transport properties. From the analysis of dispersion by Taylor (Reference Taylor1922), operator notions of mixing from Knobloch (Reference Knobloch1977), computations of ‘effective diffusivity’ by Avellaneda & Majda (Reference Avellaneda and Majda1991), simplified models of turbulence by Pope (Reference Pope2011), rigorous notions of mixing in terms of Sobolev norms by Thiffeault (Reference Thiffeault2012) or upper bounds on transport of Hassanzadeh, Chini & Doering (Reference Hassanzadeh, Chini and Doering2014), a variety of different approaches have been developed to elucidate fundamental properties of turbulence.
In addition to furthering our understanding of turbulence, there are practical applications for turbulence closures. In particular, Earth Systems Models require closure relations for the transport of unresolved motions (Schneider et al. Reference Schneider, Lan, Stuart and Teixeira2017); however, the closure relations are marred by structural and parametric uncertainty, requiring ad hoc tuning to compensate for biases. Structural biases are associated with scaling laws and closure assumptions between turbulent fluxes and gradients. Modern studies are bridging the gap by incorporating more complex physics and novel scaling laws, see as examples the works of Tan et al. (Reference Tan, Kaul, Pressel, Cohen, Schneider and Teixeira2018) and Gallet & Ferrari (Reference Gallet and Ferrari2020), but the correct functional forms to represent fluxes still need to be discovered.
The multi-scale nature of turbulent flows, coherent structures and the interconnection of reacting chemical species and prognostic fields suggest that fluxes are better modelled using nonlinear and non-local operators in space, time and state. Data-driven methods relying on flexible interpolants can significantly reduce structural bias, but often at the expense of interpretability, generalizability or efficiency. Thus, understanding scaling laws and functional forms of turbulence closures is still necessary to physically constrain data-driven methods and decrease their computational expense. A promising avenue for significant progress, lying at the intersection of theory and practice, is the calculation of closure relations for passive tracers.
The present work addresses a fundamentally different question than that of short-time Lagrangian statistics, such as the works of Taylor (Reference Taylor1922), Moffatt (Reference Moffatt1983), Weeks, Urbach & Swinney (Reference Weeks, Urbach and Swinney1996) and Falkovich, Gawȩ dzki & Vergassola (Reference Falkovich, Gawȩ dzki and Vergassola2001), since our focus is on Eulerian statistically steady statistics. Consequently, we develop new non-perturbative techniques to address the question at hand. In particular, the use of path integrals or Taylor expansions is stymied since perturbation methods based on local information often yield irredeemably non-convergent expansions for strong flow fields and long time limits. The calculations herein are more akin to calculating a ground state in quantum mechanics rather than short-time particle scattering.
A middle ground is the work of Gorbunova et al. (Reference Gorbunova, Pagani, Balarac, Canet and Rossetto2021), which analyses short-time Eulerian two-point statistics and makes connections to the Lagrangian approach. There they use renormalization groups as the workhorse for calculations. The most similar prior work regarding problem formulation is the upper bound analysis of Hakulinen (Reference Hakulinen2003), in which all moments of a stochastically advected passive tracer were considered. The scope was different because the goal was to understand all moments of the resulting stochastic tracer field advected by the Gaussian model of Kraichnan (Reference Kraichnan1968). Here we focus on exact expressions for the ensemble mean flux caused by a general class of flow fields. Although we only focus on the ensemble mean flux of a passive tracer, we do not make restrictions on the temporal statistics of the stochastic flow field. Furthermore, the methodology we outline extends to other moments of the flow field and short-time statistics, although we emphasize neither.
We make arguments akin to those by Kraichnan (Reference Kraichnan1968) to motivate the operator approach, but our calculation method is fundamentally different. Given that the goal is to construct an operator rather than estimate a diffusivity tensor acting on the ensemble mean gradients or deriving upper bounds, we take a field-theoretic perspective (Hopf Reference Hopf1952). Doing so allows us to derive a coupled set of partial differential equations representing conditional mean tracers where the conditional averages are with respect to different flow states. The flux associated with fluctuations is then a Schur complement of the resulting linear system with respect to statistical ‘perturbation’ variables. Moreover, if the flow statistics are given by a continuous-time Markov process with a small finite state space, the Schur complement becomes tractable to compute analytically. Hereafter, we refer to the flux associated with fluctuations as the turbulent flux (which is sometimes also called an ‘eddy flux’), and the corresponding operator is the turbulent diffusivity operator (alternatively an ‘effective diffusivity operator’).
The paper is organized as follows. In § 2, we formulate the closure problem and recast it as one of solving partial differential equations. In § 3, we give two examples: a one-dimensional (1-D) tracer advected by an Ornstein–Uhlenbeck process and a tracer advected by a flow field with an arbitrary spatial structure that switches between three states. Section 4 outlines the general theory, and we apply it to a travelling stochastic wave in a channel in § 5. Appendices supplement the body of the manuscript. Appendix A shows how a ‘white-noise’ limit reduces the turbulent diffusivity to a local diffusivity tensor and how the present theory encompasses the class of flow fields of Kraichnan (Reference Kraichnan1968) in the ‘white-noise’ limit. Appendix B provides a direct field-theoretic derivation of arguments in § 2, and Appendix C provides a heuristic overview of obtaining continuous-time Markov processes with finite state space and their statistics from deterministic or stochastic dynamical systems.
2. Problem formulation
We consider the advection and diffusion of an ensemble of passive tracers ![]() $\theta _{\omega }$
$\theta _{\omega }$
by a stochastic flow field ![]() $\boldsymbol {\tilde {u}}_{\omega } (\boldsymbol {x}, t)$ where
$\boldsymbol {\tilde {u}}_{\omega } (\boldsymbol {x}, t)$ where ![]() $\omega$ labels the ensemble member. Here,
$\omega$ labels the ensemble member. Here, ![]() $s$ is a deterministic mean zero source term and
$s$ is a deterministic mean zero source term and ![]() $\kappa$ is a diffusivity constant. (For laboratory flows,
$\kappa$ is a diffusivity constant. (For laboratory flows, ![]() $\kappa$ would be the molecular diffusivity; for larger-scale problems, we rely on the fact that away from boundaries, the ensemble mean advective flux (but not necessarily other statistics) may still be much larger than the diffusive flux. Thus, the exact value of
$\kappa$ would be the molecular diffusivity; for larger-scale problems, we rely on the fact that away from boundaries, the ensemble mean advective flux (but not necessarily other statistics) may still be much larger than the diffusive flux. Thus, the exact value of ![]() $\kappa$ will not matter.) Our target is to obtain a meaningful equation for the ensemble mean,
$\kappa$ will not matter.) Our target is to obtain a meaningful equation for the ensemble mean,
which requires a computationally amenable expression for the mean advective flux, ![]() $\langle \boldsymbol {\tilde {u}} \theta \rangle$, in terms of the statistics of the flow field,
$\langle \boldsymbol {\tilde {u}} \theta \rangle$, in terms of the statistics of the flow field, ![]() $\boldsymbol {\tilde {u}}_{\omega } (\boldsymbol {x}, t)$, and the ensemble average of the tracer,
$\boldsymbol {\tilde {u}}_{\omega } (\boldsymbol {x}, t)$, and the ensemble average of the tracer, ![]() $\langle \theta \rangle$. Thus, the closure problem is to find an operator
$\langle \theta \rangle$. Thus, the closure problem is to find an operator ![]() ${O}$ that relates the ensemble mean,
${O}$ that relates the ensemble mean, ![]() $\langle \theta \rangle$, to the ensemble mean advective-flux,
$\langle \theta \rangle$, to the ensemble mean advective-flux, ![]() $\langle \boldsymbol {\tilde {u}} \theta \rangle$, i.e.
$\langle \boldsymbol {\tilde {u}} \theta \rangle$, i.e.
We show how to define (and solve for) the operator ![]() ${O}$. We do so by writing down the Fokker–Planck/master equation for the joint Markov process
${O}$. We do so by writing down the Fokker–Planck/master equation for the joint Markov process ![]() $(\boldsymbol {\tilde {u}}_{\omega } , \theta _{\omega })$ corresponding to (2.1), integrating with respect to all possible tracer field configurations and manipulating the resulting system of partial differential equations. The operator will be linear with respect to its argument and depend on the statistics of the flow field.
$(\boldsymbol {\tilde {u}}_{\omega } , \theta _{\omega })$ corresponding to (2.1), integrating with respect to all possible tracer field configurations and manipulating the resulting system of partial differential equations. The operator will be linear with respect to its argument and depend on the statistics of the flow field.
We assume all tracer ensemble members to have the same initial condition and, thus, the ensemble average here is with respect to different flow realizations. The only source of randomness comes from different flow realizations. Throughout the manuscript, we assume homogeneous Neumann boundary conditions for the tracer and zero wall-normal flow for the velocity field when boundaries are present. Combined with the assumption that the source term is mean zero, these restrictions imply that the tracer average is conserved.
For the statistics of the flow field, we consider a continuous-time Markov process with known statistics, as characterized by the generator of the process. When the state space of the flow is finite with ![]() $N$ states, we label all possible flow configurations corresponding to steady flow fields by
$N$ states, we label all possible flow configurations corresponding to steady flow fields by ![]() $\boldsymbol {u}_n(\boldsymbol {x})$, where
$\boldsymbol {u}_n(\boldsymbol {x})$, where ![]() $n$ is the associated state index. We will keep with the convention of using the
$n$ is the associated state index. We will keep with the convention of using the ![]() $\boldsymbol {\tilde {u}}$ as a dynamic variable and
$\boldsymbol {\tilde {u}}$ as a dynamic variable and ![]() $\boldsymbol {u}$ as a fixed flow structure. These choices represent the flow as a Markov jump process where the jumps occur between flow fields with a fixed spatial structure.
$\boldsymbol {u}$ as a fixed flow structure. These choices represent the flow as a Markov jump process where the jumps occur between flow fields with a fixed spatial structure.
Physically, we think of these states as representing coherent structures in a turbulent flow. (This is viewed as a finite volume discretization in function space where the states are the ‘cell averages’ of a control volume in function space. Thus, the transition probability matrix becomes an approximated Perron–Frobenius operator of the turbulent flow.) Suri et al. (Reference Suri, Tithof, Grigoriev and Schatz2017) provide the experimental and numerical motivation for this philosophy in the context of an approximate Kolmogorov flow. By its very nature, a turbulent flow that is chaotic and unpredictable over long time horizons is modelled as being semi-unpredictable through our choice. Over short horizons, the probability of remaining in a given state is large. The flow is limited to moving to a subset of likely places in phase space in the medium term. Over long time horizons, the most one can say about the flow is related to the likelihood of being found in the appropriate subset of phase space associated with the statistically steady state.
Thus, we proceed by characterizing the probability, ![]() $\mathbb {P}$, of transitioning from state
$\mathbb {P}$, of transitioning from state ![]() $n$ to state
$n$ to state ![]() $m$ by a transition matrix
$m$ by a transition matrix ![]() $\mathscr {P}(\tau )$,
$\mathscr {P}(\tau )$,
The transition probability is defined through its relation to the generator ![]() $\mathcal {Q}$,
$\mathcal {Q}$,
where ![]() $\exp ( \mathcal {Q} \tau )$ is a matrix exponential. Each entry of
$\exp ( \mathcal {Q} \tau )$ is a matrix exponential. Each entry of ![]() $\mathscr {P}(\tau )$ must be positive. Furthermore, for each
$\mathscr {P}(\tau )$ must be positive. Furthermore, for each ![]() $\tau$, the columns of
$\tau$, the columns of ![]() $\mathscr {P}(\tau )$ sum to one since the total probability must always sum to one. Similarly,
$\mathscr {P}(\tau )$ sum to one since the total probability must always sum to one. Similarly, ![]() $\mathcal {Q}$'s off-diagonal terms must be positive and the column sum of
$\mathcal {Q}$'s off-diagonal terms must be positive and the column sum of ![]() $\mathcal {Q}$ must be zero. (Indeed, to first order,
$\mathcal {Q}$ must be zero. (Indeed, to first order, ![]() $\exp (\mathcal {Q} \,{\rm d}t) = \mathbb {I} + \mathcal {Q} \,{\rm d}t$. The positivity requirement of the transition probability
$\exp (\mathcal {Q} \,{\rm d}t) = \mathbb {I} + \mathcal {Q} \,{\rm d}t$. The positivity requirement of the transition probability ![]() $\mathscr {P}({\rm d}t)=\exp (\mathcal {Q} \,{\rm d}t)$ necessitates the positivity of
$\mathscr {P}({\rm d}t)=\exp (\mathcal {Q} \,{\rm d}t)$ necessitates the positivity of ![]() $\mathcal {Q}$'s off-diagonal terms and thus, in turn, the negativity of its diagonal terms.)
$\mathcal {Q}$'s off-diagonal terms and thus, in turn, the negativity of its diagonal terms.)
We denote the probability of an ensemble member, ![]() $\boldsymbol {\tilde {u}}_{\omega }$, being found at state
$\boldsymbol {\tilde {u}}_{\omega }$, being found at state ![]() $m$ at time
$m$ at time ![]() $t$ by
$t$ by ![]() $\mathcal {P}_m(t)$,
$\mathcal {P}_m(t)$,
The evolution equation for ![]() $\mathcal {P}_m(t)$ is the master equation,
$\mathcal {P}_m(t)$ is the master equation,
We assume that (2.7) has a unique steady state and denote the components of the steady state by ![]() $P_m$.
$P_m$.
We have used several ‘P’ at this stage, and their relation is:
(i)
 $\mathbb {P}$ denotes a probability;
$\mathbb {P}$ denotes a probability;(ii)
 $\mathscr {P}(\tau )$ denotes the transition probability matrix for a time
$\mathscr {P}(\tau )$ denotes the transition probability matrix for a time  $\tau$ in the future;
$\tau$ in the future;(iii)
 $\mathcal {P}_m(t)$ denotes the probability of being in state
$\mathcal {P}_m(t)$ denotes the probability of being in state  $m$ at time
$m$ at time  $t$. The algebraic relation
(2.8)holds;
$t$. The algebraic relation
(2.8)holds; \begin{equation} \sum_m \mathcal{P}_m(t+\tau) \boldsymbol{\hat{e}}_m = \mathscr{P}(\tau) \sum_n \mathcal{P}_n(t) \boldsymbol{\hat{e}}_n \end{equation}
\begin{equation} \sum_m \mathcal{P}_m(t+\tau) \boldsymbol{\hat{e}}_m = \mathscr{P}(\tau) \sum_n \mathcal{P}_n(t) \boldsymbol{\hat{e}}_n \end{equation}(iv) in addition, we use
 $P_m$ for the statistically steady probability of being found in state
$P_m$ for the statistically steady probability of being found in state  $m$, in the limit
(2.9)
$m$, in the limit
(2.9) \begin{equation} \lim_{t \rightarrow \infty} \mathcal{P}_m(t) = P_m . \end{equation}
\begin{equation} \lim_{t \rightarrow \infty} \mathcal{P}_m(t) = P_m . \end{equation}
We exploit the information about the flow field to infer the mean statistics of the passive tracer ![]() $\theta _\omega$. We do so by conditionally averaging the tracer field
$\theta _\omega$. We do so by conditionally averaging the tracer field ![]() $\theta _\omega$ with respect to a given flow state
$\theta _\omega$ with respect to a given flow state ![]() $\boldsymbol {u}_m$. More precisely, given the stochastic partial differential equation,
$\boldsymbol {u}_m$. More precisely, given the stochastic partial differential equation,
we shall obtain equations for probability weighted conditional means of ![]() $\theta _\omega$,
$\theta _\omega$,
Empirically, the probability weighted conditional average is computed by examining all ensemble members at a fixed time step, adding up only the ensemble members that are currently being advected by state ![]() $\boldsymbol {u}_m$ and then dividing by the total number of ensemble members. We will show that the evolution equation for
$\boldsymbol {u}_m$ and then dividing by the total number of ensemble members. We will show that the evolution equation for ![]() $\varTheta _m$ is
$\varTheta _m$ is
As we shall see, the explicit dependence on the generator in (2.14) yields considerable information. We recover the equation for the tracer ensemble mean, (2.2), by summing (2.14) over the index ![]() $m$, using
$m$, using ![]() $\langle \theta \rangle = \sum _m \varTheta _m$,
$\langle \theta \rangle = \sum _m \varTheta _m$, ![]() $\sum _m \mathcal {Q}_{mn} = \boldsymbol {0}$, and
$\sum _m \mathcal {Q}_{mn} = \boldsymbol {0}$, and ![]() $\sum _m \mathcal {P}_{m} = 1$,
$\sum _m \mathcal {P}_{m} = 1$,
 \begin{align} \partial_t \sum_m \varTheta_m + \boldsymbol{\nabla} \boldsymbol{\cdot} \left( \sum_m \boldsymbol{u}_m \varTheta_m - \kappa \boldsymbol{\nabla} \sum_m \varTheta_m \right) &= s(\boldsymbol{x}) \end{align}
\begin{align} \partial_t \sum_m \varTheta_m + \boldsymbol{\nabla} \boldsymbol{\cdot} \left( \sum_m \boldsymbol{u}_m \varTheta_m - \kappa \boldsymbol{\nabla} \sum_m \varTheta_m \right) &= s(\boldsymbol{x}) \end{align}The presence of the generator when taking conditional averages is similar to the entrainment hypothesis in the atmospheric literature. See, for example, Tan et al. (Reference Tan, Kaul, Pressel, Cohen, Schneider and Teixeira2018) for its use in motivating a turbulence closure; however, here, we derive the result from the direct statistical representation instead of hypothesizing its presence from a dynamical argument.
We give a brief derivation of (2.13) and (2.14) using a discretization of the advection-diffusion equation here. For an alternative derivation where we forego discretization, see Appendix B, and for a brief overview of the connection between the discrete, continuous and mixed master equation, see Appendix C or, in a simpler context, the work of Hagan, Doering & Levermore (Reference Hagan, Doering and Levermore1989). Most of the terms in (2.14) are obtained by applying a conditional average to (2.11), commuting with spatial derivatives when necessary and then multiplying through by ![]() $\mathcal {P}_m$; however, the primary difficulty lies in proper treatment of the conditional average of the temporal derivative. We circumvent the problem in a roundabout manner: discretize the advection-diffusion equation, write down the resulting master equation, compute moments of the probability distribution and then take limits to restore the continuum nature of the advection-diffusion equation.
$\mathcal {P}_m$; however, the primary difficulty lies in proper treatment of the conditional average of the temporal derivative. We circumvent the problem in a roundabout manner: discretize the advection-diffusion equation, write down the resulting master equation, compute moments of the probability distribution and then take limits to restore the continuum nature of the advection-diffusion equation.
A generic discretization (in any number of dimensions) of (2.11) is of the form
 \begin{equation} \frac{{\rm d}}{{\rm d}t} \theta^i + \sum_{jkc} A_{ijk}^c \tilde{u}^{k,c}_\omega \theta^j - \sum_j D_{ij} \theta^j = s^i \end{equation}
\begin{equation} \frac{{\rm d}}{{\rm d}t} \theta^i + \sum_{jkc} A_{ijk}^c \tilde{u}^{k,c}_\omega \theta^j - \sum_j D_{ij} \theta^j = s^i \end{equation}
for some tensor ![]() $A_{ijk}^c$, representing advection, and matrix
$A_{ijk}^c$, representing advection, and matrix ![]() $D_{ij}$, representing diffusion. Here, each
$D_{ij}$, representing diffusion. Here, each ![]() $i,j$ and
$i,j$ and ![]() $k$ corresponds to a spatial location, and the index
$k$ corresponds to a spatial location, and the index ![]() $c$ corresponds to a component of the velocity field
$c$ corresponds to a component of the velocity field ![]() $\boldsymbol {\tilde {u}}$. The variable
$\boldsymbol {\tilde {u}}$. The variable ![]() $\theta ^i$ is the value of the tracer at grid location
$\theta ^i$ is the value of the tracer at grid location ![]() $i$ and
$i$ and ![]() $v^{k,c}$ is the value of the
$v^{k,c}$ is the value of the ![]() $c$th velocity component and grid location
$c$th velocity component and grid location ![]() $k$. The master equation for the joint probability density for each component
$k$. The master equation for the joint probability density for each component ![]() $\theta ^i$ and Markov state
$\theta ^i$ and Markov state ![]() $m$,
$m$, ![]() $\rho _m( \boldsymbol {\theta } )$, where
$\rho _m( \boldsymbol {\theta } )$, where ![]() $\boldsymbol {\theta } = (\theta ^1, \theta ^2,\ldots )$ and the
$\boldsymbol {\theta } = (\theta ^1, \theta ^2,\ldots )$ and the ![]() $m$-index denotes a particular Markov state, is a combination of the Liouville equation for (2.17) and the transition rate equation for (2.10),
$m$-index denotes a particular Markov state, is a combination of the Liouville equation for (2.17) and the transition rate equation for (2.10),
 \begin{equation} \partial_t \rho_m = \sum_{i} \frac{\partial}{\partial \theta^i} \left[ \left( \sum_{jkc} A_{ijk}^c u^{k,c}_m \theta^j - \sum_j D_{ij} \theta^j - s^i \right ) \rho_m \right] + \sum_n \mathcal{Q}_{mn} \rho_n . \end{equation}
\begin{equation} \partial_t \rho_m = \sum_{i} \frac{\partial}{\partial \theta^i} \left[ \left( \sum_{jkc} A_{ijk}^c u^{k,c}_m \theta^j - \sum_j D_{ij} \theta^j - s^i \right ) \rho_m \right] + \sum_n \mathcal{Q}_{mn} \rho_n . \end{equation}Define the following moments:
We obtain an equation for ![]() $\mathcal {P}_m$ by integrating (2.18) by
$\mathcal {P}_m$ by integrating (2.18) by ![]() ${\rm d}\boldsymbol {\theta }$ to yield
${\rm d}\boldsymbol {\theta }$ to yield
as expected from (2.7). The equation for ![]() $\varTheta _m^\ell$ is obtained by multiplying (2.18) by
$\varTheta _m^\ell$ is obtained by multiplying (2.18) by ![]() $\theta ^\ell$ and then integrating with respect to
$\theta ^\ell$ and then integrating with respect to ![]() ${\rm d}\boldsymbol {\theta }$,
${\rm d}\boldsymbol {\theta }$,
 \begin{equation} \frac{{\rm d}}{{\rm d}t} \varTheta_m^\ell ={-}\sum_{jkc} A_{\ell jk}^c u^{k,c}_m \varTheta^j_m + \sum_j D_{\ell j} \varTheta^j_m + s^\ell \mathcal{P}_m + \sum_n \mathcal{Q}_{mn} \varTheta_n^\ell , \end{equation}
\begin{equation} \frac{{\rm d}}{{\rm d}t} \varTheta_m^\ell ={-}\sum_{jkc} A_{\ell jk}^c u^{k,c}_m \varTheta^j_m + \sum_j D_{\ell j} \varTheta^j_m + s^\ell \mathcal{P}_m + \sum_n \mathcal{Q}_{mn} \varTheta_n^\ell , \end{equation}
where we integrated by parts on the ![]() $\int \,{\rm d} \boldsymbol {\theta } \theta ^\ell \partial _{\theta ^i} \bullet$ term. Upon taking limits of (2.21), we arrive at (2.13) and (2.14), repeated here for convenience,
$\int \,{\rm d} \boldsymbol {\theta } \theta ^\ell \partial _{\theta ^i} \bullet$ term. Upon taking limits of (2.21), we arrive at (2.13) and (2.14), repeated here for convenience,
We compare (2.23) to the direct application of the conditional average to (2.11) followed by multiplication with ![]() $\mathcal {P}_m$ to infer
$\mathcal {P}_m$ to infer
In summary, for an ![]() $m$-dimensional advection-diffusion equation and
$m$-dimensional advection-diffusion equation and ![]() $N$ Markov states, (2.13) and (2.14) are a set of
$N$ Markov states, (2.13) and (2.14) are a set of ![]() $N$-coupled
$N$-coupled ![]() $m$-dimensional advection-diffusion equations with
$m$-dimensional advection-diffusion equations with ![]() $N$ different steady velocities. When
$N$ different steady velocities. When ![]() $c$ continuous variables describe the statistics of the flow field, the resulting equation set becomes an
$c$ continuous variables describe the statistics of the flow field, the resulting equation set becomes an ![]() $m+c$ dimensional system. Stated differently, if the statistics of
$m+c$ dimensional system. Stated differently, if the statistics of ![]() $\boldsymbol {\tilde {u}}_{\omega }$ are characterized by transitions between a continuum of states associated with variables
$\boldsymbol {\tilde {u}}_{\omega }$ are characterized by transitions between a continuum of states associated with variables ![]() $\boldsymbol {\alpha } \in \mathbb {R}^c$ and Fokker–Planck operator
$\boldsymbol {\alpha } \in \mathbb {R}^c$ and Fokker–Planck operator ![]() $\mathcal {F}_{\boldsymbol {\alpha }}$, then the conditional averaging procedure yields
$\mathcal {F}_{\boldsymbol {\alpha }}$, then the conditional averaging procedure yields
where ![]() $\mathcal {P} = \mathcal {P}(\boldsymbol {\alpha }, t)$,
$\mathcal {P} = \mathcal {P}(\boldsymbol {\alpha }, t)$, ![]() $\varTheta = \varTheta (\boldsymbol {x}, \boldsymbol {\alpha }, t)$ and
$\varTheta = \varTheta (\boldsymbol {x}, \boldsymbol {\alpha }, t)$ and ![]() $\boldsymbol {u} = \boldsymbol {u}(\boldsymbol {x}, \boldsymbol {\alpha })$. Equations (2.22) and (2.23) are thought of as finite volume discretizations of flow statistics in (2.25) and (2.26). We give an explicit example in § 3.1 and another in § 5.
$\boldsymbol {u} = \boldsymbol {u}(\boldsymbol {x}, \boldsymbol {\alpha })$. Equations (2.22) and (2.23) are thought of as finite volume discretizations of flow statistics in (2.25) and (2.26). We give an explicit example in § 3.1 and another in § 5.
Our primary concern in this work is to use (2.22) and (2.23), or analogously (2.25) and (2.26), to calculate meaningful expressions for ![]() $\langle \boldsymbol {\tilde {u}} \theta \rangle$; however, we shall first take a broader view to understand the general structure of the turbulent fluxes. We attribute the following argument to Weinstock (Reference Weinstock1969) but use different notation and make additional simplifications.
$\langle \boldsymbol {\tilde {u}} \theta \rangle$; however, we shall first take a broader view to understand the general structure of the turbulent fluxes. We attribute the following argument to Weinstock (Reference Weinstock1969) but use different notation and make additional simplifications.
Applying the Reynolds decomposition
yields
The perturbation equation is rewritten as
This equation is an infinite system (or finite, depending on the number of ensemble members) of coupled partial differential equations between the different ensemble members. The ensemble members are coupled due to the turbulent flux, ![]() $\langle \boldsymbol {\tilde {u}}' \theta ' \rangle$. The key observation is to notice that the terms on the left-hand side involve the perturbation variables and not the ensemble mean of the gradients. Assuming it is possible to find the inverse, the Green's function for the large linear system is used to yield
$\langle \boldsymbol {\tilde {u}}' \theta ' \rangle$. The key observation is to notice that the terms on the left-hand side involve the perturbation variables and not the ensemble mean of the gradients. Assuming it is possible to find the inverse, the Green's function for the large linear system is used to yield
where we also have to integrate with respect to the measure defining the different ensemble members through ![]() ${\rm d}\mu _{\omega '}$. In our notation, this implies
${\rm d}\mu _{\omega '}$. In our notation, this implies ![]() $\langle \theta \rangle = \int \,{\rm d} \mu _{\omega } \theta _\omega$. We use this expression to rewrite the turbulent flux as
$\langle \theta \rangle = \int \,{\rm d} \mu _{\omega } \theta _\omega$. We use this expression to rewrite the turbulent flux as
We make two simplifications for illustrative purposes.
(i) All ensemble averages are independent of time.
(ii) The flow is incompressible, i.e.
 $\boldsymbol {\nabla } \boldsymbol {\cdot } \boldsymbol {\tilde {u}} = 0$.
$\boldsymbol {\nabla } \boldsymbol {\cdot } \boldsymbol {\tilde {u}} = 0$.
Equation (2.32) becomes
We perform the ![]() $t', \alpha, \omega$ integrals first to define the turbulent diffusivity tensor kernel as
$t', \alpha, \omega$ integrals first to define the turbulent diffusivity tensor kernel as
 \begin{align} \langle \boldsymbol{\tilde{u}}' \theta' \rangle &={-}\int \,{\rm d}\boldsymbol{x}' \underbrace{\int \,{\rm d}t' \,{\rm d}\mu_{\omega} \,{\rm d}\mu_{\omega'} \left[ \boldsymbol{\tilde{u}}'_\omega(\boldsymbol{x}, t) \otimes \boldsymbol{\tilde{u}}_{\omega'}'(\boldsymbol{x}' , t') \mathcal{G}_{\omega \omega'}(\boldsymbol{x}, t | \boldsymbol{x}' , t' ) \right] }_{\boldsymbol{\mathcal{K}}(\boldsymbol{x}|\boldsymbol{x}')} \boldsymbol{\cdot} \boldsymbol{\nabla} \langle \theta \rangle (\boldsymbol{x}' ), \end{align}
\begin{align} \langle \boldsymbol{\tilde{u}}' \theta' \rangle &={-}\int \,{\rm d}\boldsymbol{x}' \underbrace{\int \,{\rm d}t' \,{\rm d}\mu_{\omega} \,{\rm d}\mu_{\omega'} \left[ \boldsymbol{\tilde{u}}'_\omega(\boldsymbol{x}, t) \otimes \boldsymbol{\tilde{u}}_{\omega'}'(\boldsymbol{x}' , t') \mathcal{G}_{\omega \omega'}(\boldsymbol{x}, t | \boldsymbol{x}' , t' ) \right] }_{\boldsymbol{\mathcal{K}}(\boldsymbol{x}|\boldsymbol{x}')} \boldsymbol{\cdot} \boldsymbol{\nabla} \langle \theta \rangle (\boldsymbol{x}' ), \end{align}
The independence of ![]() $\boldsymbol {\mathcal {K}}$ with respect to
$\boldsymbol {\mathcal {K}}$ with respect to ![]() $t$ follows from the time-independence of
$t$ follows from the time-independence of ![]() $\langle \boldsymbol {\tilde {u}}' \theta ' \rangle$ and
$\langle \boldsymbol {\tilde {u}}' \theta ' \rangle$ and ![]() $\langle \theta \rangle$. In total, we see
$\langle \theta \rangle$. In total, we see
An insight from (2.36) is the dependence of turbulent fluxes ![]() $\langle \boldsymbol {\tilde {u}}' \theta ' \rangle$ at location
$\langle \boldsymbol {\tilde {u}}' \theta ' \rangle$ at location ![]() $\boldsymbol {x}$ as a weighted sum of gradients of the mean variable
$\boldsymbol {x}$ as a weighted sum of gradients of the mean variable ![]() $\langle \theta \rangle$ at locations
$\langle \theta \rangle$ at locations ![]() $\boldsymbol {x}'$. The operator is linear and amenable to computation, even in turbulent flows (Bhamidipati, Souza & Flierl Reference Bhamidipati, Souza and Flierl2020).
$\boldsymbol {x}'$. The operator is linear and amenable to computation, even in turbulent flows (Bhamidipati, Souza & Flierl Reference Bhamidipati, Souza and Flierl2020).
We consider the spectrum for the turbulent diffusivity operator ![]() $\int \,{\rm d} \boldsymbol {x}' \mathcal {K}(\boldsymbol {x} | \boldsymbol {x}' ) \bullet$ as a characterization of turbulent mixing by the flow field
$\int \,{\rm d} \boldsymbol {x}' \mathcal {K}(\boldsymbol {x} | \boldsymbol {x}' ) \bullet$ as a characterization of turbulent mixing by the flow field ![]() $\boldsymbol {\tilde {u}}_{\omega } (\boldsymbol {x}, t)$. We comment that the operator
$\boldsymbol {\tilde {u}}_{\omega } (\boldsymbol {x}, t)$. We comment that the operator ![]() $\int \,{\rm d} \boldsymbol {x}' \mathcal {K}(\boldsymbol {x} | \boldsymbol {x}' ) \bullet$ is a mapping from vector fields to vector fields, whereas the kernel
$\int \,{\rm d} \boldsymbol {x}' \mathcal {K}(\boldsymbol {x} | \boldsymbol {x}' ) \bullet$ is a mapping from vector fields to vector fields, whereas the kernel ![]() $\mathcal {K}(\boldsymbol {x} | \boldsymbol {x}' )$ is a mapping from two positions to a tensor.
$\mathcal {K}(\boldsymbol {x} | \boldsymbol {x}' )$ is a mapping from two positions to a tensor.
For example, consider a 1-D problem in a periodic domain ![]() $x \in [0, 2 {\rm \pi})$. If
$x \in [0, 2 {\rm \pi})$. If ![]() $\mathcal {K}(x | x' ) = \kappa _e \delta (x - x')$ for some positive constant
$\mathcal {K}(x | x' ) = \kappa _e \delta (x - x')$ for some positive constant ![]() $\kappa _e$, the spectrum of the operator is flat and turbulent mixing remains the same on every length scale. If
$\kappa _e$, the spectrum of the operator is flat and turbulent mixing remains the same on every length scale. If ![]() $\mathcal {K}(x| x' ) = -\kappa _e \partial _{xx}^2 \delta (x - x')$, then the rate of mixing increases with increasing wavenumber and one gets hyperdiffusion. Lastly, if
$\mathcal {K}(x| x' ) = -\kappa _e \partial _{xx}^2 \delta (x - x')$, then the rate of mixing increases with increasing wavenumber and one gets hyperdiffusion. Lastly, if ![]() $\int \,{{\rm d} x}' \mathcal {K}(x | x' ) \bullet = (\kappa _e - \partial _{xx})^{-1}$, then the kernel is non-local and the rate of mixing decreases at smaller length scales.
$\int \,{{\rm d} x}' \mathcal {K}(x | x' ) \bullet = (\kappa _e - \partial _{xx})^{-1}$, then the kernel is non-local and the rate of mixing decreases at smaller length scales.
In the following section, we calculate ![]() $\int \,{\rm d} \boldsymbol {x}' \mathcal {K}(\boldsymbol {x} | \boldsymbol {x}' ) \bullet$ directly from the conditional equations, discuss the general structure in § 4 and then apply the methodology to a wandering wave in a channel in § 5.
$\int \,{\rm d} \boldsymbol {x}' \mathcal {K}(\boldsymbol {x} | \boldsymbol {x}' ) \bullet$ directly from the conditional equations, discuss the general structure in § 4 and then apply the methodology to a wandering wave in a channel in § 5.
3. Examples
We now go through two examples to understand the implications of (2.13) and (2.14). The two examples illustrate different aspects of the conditional averaging procedure. The first aspect is the ability to approximate continuous stochastic processes as one with a finite state space, i.e. a Markov jump process. The second aspect is to obtain closed-form formulae for a Markov jump process. In both cases, we use the methodology to calculate turbulent diffusivities for statistically steady states.
The first example is the advection of a passive tracer in a 1-D periodic domain by an Ornstein–Uhlenbeck process: perhaps the simplest class of problems amenable to detailed analysis. See Pappalettera (Reference Pappalettera2022) for a mathematical treatment of this problem without source terms. The second example further builds intuition for the statistical significance of the conditionally averaging procedure by examining a three-velocity state approximation to an Ornstein–Uhlenbeck in an abstract ![]() $n$-dimensional setting and a concrete two-dimensional (2-D) setting.
$n$-dimensional setting and a concrete two-dimensional (2-D) setting.
3.1. Ornstein–Uhlenbeck process in one dimension
Consider the advection of a 1-D tracer by an Ornstein–Uhlenbeck (OU) process in a ![]() $2 {\rm \pi}$ periodic domain. The equations of motion are
$2 {\rm \pi}$ periodic domain. The equations of motion are
where ![]() $s$ is a mean zero source,
$s$ is a mean zero source, ![]() $\omega$ labels the ensemble member and we choose
$\omega$ labels the ensemble member and we choose ![]() $\kappa = 0.01$ for the diffusivity constant. We shall calculate the turbulent diffusivity operator for this system in two different ways. The first will be by simulating the equations and the second will be by using numerical approximations of the conditional mean equations.
$\kappa = 0.01$ for the diffusivity constant. We shall calculate the turbulent diffusivity operator for this system in two different ways. The first will be by simulating the equations and the second will be by using numerical approximations of the conditional mean equations.
Since the flow field ![]() $u$ is independent of the spatial variable and the domain is periodic, we decompose the tracer equation using Fourier modes and calculate a diffusivity as a function of wavenumber
$u$ is independent of the spatial variable and the domain is periodic, we decompose the tracer equation using Fourier modes and calculate a diffusivity as a function of wavenumber ![]() $k$, wavenumber by wavenumber. Decomposing
$k$, wavenumber by wavenumber. Decomposing ![]() $\theta _\omega$ as
$\theta _\omega$ as
 \begin{equation} \theta_\omega(x, t) = \sum_{n={-}\infty}^{\infty} \hat{\theta}^n_\omega(t) {\rm e}^{{\rm i} k_n x} \quad\text{and}\quad s(x) = \sum_{n={-}\infty}^{\infty} \hat{s}^n {\rm e}^{{\rm i} k_n x}, \end{equation}
\begin{equation} \theta_\omega(x, t) = \sum_{n={-}\infty}^{\infty} \hat{\theta}^n_\omega(t) {\rm e}^{{\rm i} k_n x} \quad\text{and}\quad s(x) = \sum_{n={-}\infty}^{\infty} \hat{s}^n {\rm e}^{{\rm i} k_n x}, \end{equation}
where ![]() $k_n = n$, yields
$k_n = n$, yields
which are ordinary differential equations for each wavenumber ![]() $k_n$ with no coupling between wavenumbers. We define a ‘turbulent diffusivity’ on a wavenumber by wavenumber basis with
$k_n$ with no coupling between wavenumbers. We define a ‘turbulent diffusivity’ on a wavenumber by wavenumber basis with
 \begin{equation} \kappa_T(k_n) ={-}\frac{\langle \tilde{u} \hat{\theta}^n \rangle}{\langle {\rm i} k_n \hat{\theta}^n \rangle}, \end{equation}
\begin{equation} \kappa_T(k_n) ={-}\frac{\langle \tilde{u} \hat{\theta}^n \rangle}{\langle {\rm i} k_n \hat{\theta}^n \rangle}, \end{equation}
which is a flux divided by a gradient. A local diffusivity would be independent of wavenumber. Here the averaging operator, ![]() $\langle {\cdot } \rangle$, is an average over all ensemble members. This quantity is independent of the source wavenumber amplitude,
$\langle {\cdot } \rangle$, is an average over all ensemble members. This quantity is independent of the source wavenumber amplitude, ![]() $\hat {s}^n$, for non-zero sources and conventions for scaling the Fourier transform. With this observation in place, we take our source term to be
$\hat {s}^n$, for non-zero sources and conventions for scaling the Fourier transform. With this observation in place, we take our source term to be ![]() $s(x) = \delta (x) - 1$ so that
$s(x) = \delta (x) - 1$ so that ![]() $\hat {s}^n = 1$ for all
$\hat {s}^n = 1$ for all ![]() $n \neq 0$ and
$n \neq 0$ and ![]() $\hat {s}^0 = 0$. We numerically simulate (3.1) and (3.2) in spectral space until a time
$\hat {s}^0 = 0$. We numerically simulate (3.1) and (3.2) in spectral space until a time ![]() $t=25$ using
$t=25$ using ![]() $10^6$ ensemble members and then perform the ensemble average at this fixed time. We have finished the description for the first method of calculation. We now move on to using the conditional mean equations directly.
$10^6$ ensemble members and then perform the ensemble average at this fixed time. We have finished the description for the first method of calculation. We now move on to using the conditional mean equations directly.
The conditional mean equations recover the same result as the continuous ensemble mean. We show this through numerical discretization. The conditional mean equation version of (3.1) and (3.2) is
where ![]() $\varTheta = \varTheta (x, u, t)$ and
$\varTheta = \varTheta (x, u, t)$ and ![]() $\mathcal {P} = \mathcal {P}(u, t)$. We make the observation
$\mathcal {P} = \mathcal {P}(u, t)$. We make the observation
To discretize the ![]() $u$ variable, we invoke a finite volume discretization by integrating with respect to
$u$ variable, we invoke a finite volume discretization by integrating with respect to ![]() $N = N'+1$ control volumes
$N = N'+1$ control volumes ![]() $\varOmega _m = [(2m - 1 - N') / \sqrt {N'},(2m + 1 - N') / \sqrt {N'}]$ for
$\varOmega _m = [(2m - 1 - N') / \sqrt {N'},(2m + 1 - N') / \sqrt {N'}]$ for ![]() $m = 0,\ldots, N'$, a procedure which is detailed in Appendix C.2. The result is
$m = 0,\ldots, N'$, a procedure which is detailed in Appendix C.2. The result is
where
and ![]() $\mathcal {Q}_{mm'} = ( -N' \delta _{mm'} + m' \delta _{(m+1)m'} + (N'-m')\delta _{(m-1)m'} )/2$ and
$\mathcal {Q}_{mm'} = ( -N' \delta _{mm'} + m' \delta _{(m+1)m'} + (N'-m')\delta _{(m-1)m'} )/2$ and ![]() $m = 0 ,\ldots, N'$. This approximation is the same as that used by Hagan et al. (Reference Hagan, Doering and Levermore1989) to represent the Ornstein–Uhlenbeck process by Markov jump processes, but now justified as a finite volume discretization. Observe that for
$m = 0 ,\ldots, N'$. This approximation is the same as that used by Hagan et al. (Reference Hagan, Doering and Levermore1989) to represent the Ornstein–Uhlenbeck process by Markov jump processes, but now justified as a finite volume discretization. Observe that for ![]() $N = 2$, we have a dichotomous velocity process
$N = 2$, we have a dichotomous velocity process
and for ![]() $N=3$, we have a generalization
$N=3$, we have a generalization
similar to the models of Davis et al. (Reference Davis, Flierl, Wiebe and Franks1991) and Ferrari, Manfroi & Young (Reference Ferrari, Manfroi and Young2001). The presence of an evolution equation for ![]() $\mathcal {P}_n$ accounts for statistically non-stationary states of the flow field. Alternative discretizations are possible. For example, using a spectral discretization for the
$\mathcal {P}_n$ accounts for statistically non-stationary states of the flow field. Alternative discretizations are possible. For example, using a spectral discretization for the ![]() $u$ variable via Hermite polynomials converges to the continuous system at a faster rate; however, the resulting discrete system no longer has an interpretation as a Markov jump process for three or more state variables.
$u$ variable via Hermite polynomials converges to the continuous system at a faster rate; however, the resulting discrete system no longer has an interpretation as a Markov jump process for three or more state variables.
Next, taking the Fourier transform in ![]() $x$ yields
$x$ yields
We solve for the steady-state solution
and then compute
 \begin{equation} \kappa_E(k_n)
={-}\frac{\displaystyle\sum_m u_m \hat{\varTheta}_m^n}{\displaystyle \sum_m {\rm i}
k_n \hat{\varTheta}_m^n } \Rightarrow
-\frac{\displaystyle\int_{-\infty}^\infty \,{\rm d}u \hat{\varTheta}^n u
}{\displaystyle\int_{-\infty}^\infty \,{\rm d}u ({\rm i} k_n
\hat{\varTheta}^n) } \end{equation}
\begin{equation} \kappa_E(k_n)
={-}\frac{\displaystyle\sum_m u_m \hat{\varTheta}_m^n}{\displaystyle \sum_m {\rm i}
k_n \hat{\varTheta}_m^n } \Rightarrow
-\frac{\displaystyle\int_{-\infty}^\infty \,{\rm d}u \hat{\varTheta}^n u
}{\displaystyle\int_{-\infty}^\infty \,{\rm d}u ({\rm i} k_n
\hat{\varTheta}^n) } \end{equation}
for various choices of discrete states. The calculations in the numerator and denominator are equivalent to ensemble averages.
We compare the two methods of calculation in figure 1. We see that increasing the number of states from ![]() $N=2$ to
$N=2$ to ![]() $N=15$ yields, for each wavenumber, ensemble averages similar to those of the Ornstein–Uhlenbeck process. The explicit formula for
$N=15$ yields, for each wavenumber, ensemble averages similar to those of the Ornstein–Uhlenbeck process. The explicit formula for ![]() $N=3$ is given in the next section. We stop at
$N=3$ is given in the next section. We stop at ![]() $N = 15$ states since all wavenumbers in the plot are within 1 % of one another. The
$N = 15$ states since all wavenumbers in the plot are within 1 % of one another. The ![]() $n=0$ wavenumber is plotted for convenience as well and, in the case of the present process, also happens to correspond to the velocity autocorrelation. The correspondence of all velocity states (including the Ornstein–Uhlenbeck process) at wavenumber
$n=0$ wavenumber is plotted for convenience as well and, in the case of the present process, also happens to correspond to the velocity autocorrelation. The correspondence of all velocity states (including the Ornstein–Uhlenbeck process) at wavenumber ![]() $k_n=0$ is particular to this system and is not a feature that holds in general. The ‘large scale limit’, corresponding to wavenumber
$k_n=0$ is particular to this system and is not a feature that holds in general. The ‘large scale limit’, corresponding to wavenumber ![]() $k_n = 0$, can often be considered an appropriate local diffusivity definition.
$k_n = 0$, can often be considered an appropriate local diffusivity definition.

Figure 1. Wavenumber diffusivities. We show the turbulent diffusivity estimate as a function of wavenumber. Here we see that different wavenumbers, or equivalently length scales, produce different estimates of the turbulent diffusivity. Furthermore, we show that the different N-state approximations yield an increasingly better approximation to the Ornstein–Uhlenbeck empirical estimate.
Although we use the finite volume discretization of velocity states as approximations to the Ornstein–Uhlenbeck process, they also constitute a realizable stochastic process in the form of a Markov jump process. Thus, each finite state case can be simulated from whence the turbulent diffusivity estimate in figure 1 is exact rather than an approximation. We choose a particular example with ![]() $N=3$ in the following section.
$N=3$ in the following section.
Furthermore, each wavenumber ![]() $k_n$ yields a different estimate of the turbulent diffusivity. In particular, the decrease of turbulent diffusivity as a function of wavenumber implies non-locality. Choosing a forcing that is purely sinusoidal of a given mode would yield different estimates of turbulent fluxes. For example, forcing with
$k_n$ yields a different estimate of the turbulent diffusivity. In particular, the decrease of turbulent diffusivity as a function of wavenumber implies non-locality. Choosing a forcing that is purely sinusoidal of a given mode would yield different estimates of turbulent fluxes. For example, forcing with ![]() $s(x) = \sin (x)$ would yield a diffusivity estimate of
$s(x) = \sin (x)$ would yield a diffusivity estimate of ![]() $\kappa _T(1) \approx 0.58$, whereas forcing with
$\kappa _T(1) \approx 0.58$, whereas forcing with ![]() $s(x) = \sin (2x)$ would yield a diffusivity estimate of
$s(x) = \sin (2x)$ would yield a diffusivity estimate of ![]() $\kappa _T(2) \approx 0.34$, as implied by figure 1.
$\kappa _T(2) \approx 0.34$, as implied by figure 1.
In the present case, the inverse Fourier transform of the turbulent diffusivity yields the turbulent diffusivity operator in real space. Since products in wavenumber space are circular convolutions in real space, we naturally guarantee the translation invariance of the kernel for the present case. The turbulent diffusivity kernels are shown in figure 2. Thus, the equation for the ensemble mean is
where ![]() $*$ is a circular convolution with the kernel in figure 2.
$*$ is a circular convolution with the kernel in figure 2.

Figure 2. Kernels for N-state systems. Here we show the turbulent diffusivity kernels for several approximations of the Ornstein–Uhlenbeck diffusivity kernel. We compare all kernels to the ![]() $N = 15$ state kernel, which is a good approximation to the OU process kernel. We see that the width of the kernel is comparable to the domain. The non-locality of the kernel is a consequence of the turbulent diffusivity estimate differing on a wavenumber per wavenumber basis.
$N = 15$ state kernel, which is a good approximation to the OU process kernel. We see that the width of the kernel is comparable to the domain. The non-locality of the kernel is a consequence of the turbulent diffusivity estimate differing on a wavenumber per wavenumber basis.
To illustrate the action of a non-local operator, we show the implied flux for a gradient that is presumed to have the functional form
The flux computed from the convolution with the ![]() $N=15$ state kernel
$N=15$ state kernel
is shown in figure 3. Even though the gradient changes sign, we see that the flux remains purely negative, i.e. the flux is up-gradient at particular points of the domain. Furthermore, the figure 3(b) does not resemble a straight line through the origin, as would be the case for a local diffusivity. The red portion highlights the ‘up-gradient’ part of the flux-gradient relation. We point out these features to illustrate the limitations of a purely local flux-gradient relationship.

Figure 3. Flux prediction from the kernel. Given the ensemble mean gradient (green), we convolve with the ![]() $N=15$ state kernel to get the flux (yellow) in panel (a). We see that the gradient changes sign while the flux always remains negative. To further illustrate the effect of non-locality, we show flux versus gradient in panel (b). The blue regions are down-gradient and the red regions are up-gradient. A local diffusivity estimate would be a straight line through the origin, whose slope determines the diffusivity constant.
$N=15$ state kernel to get the flux (yellow) in panel (a). We see that the gradient changes sign while the flux always remains negative. To further illustrate the effect of non-locality, we show flux versus gradient in panel (b). The blue regions are down-gradient and the red regions are up-gradient. A local diffusivity estimate would be a straight line through the origin, whose slope determines the diffusivity constant.
This section focused on a flow field with a simple spatial and temporal structure. In the next section, we derive the turbulent diffusivity operator for a flow with arbitrary spatial structure but with a simple statistical temporal structure: a three-state velocity field whose amplitude is an approximation to the Ornstein–Uhlenbeck process.
3.2. A generalized three-state system with a 2-D example
For this example, we consider a Markov process that transitions between three incompressible states ![]() $\boldsymbol {u}_1(\boldsymbol {x}) = \boldsymbol {u}(\boldsymbol {x})$,
$\boldsymbol {u}_1(\boldsymbol {x}) = \boldsymbol {u}(\boldsymbol {x})$, ![]() $\boldsymbol {u}_2(\boldsymbol {x}) = 0$ and
$\boldsymbol {u}_2(\boldsymbol {x}) = 0$ and ![]() $\boldsymbol {u}_3(\boldsymbol {x}) = -\boldsymbol {u}(\boldsymbol {x})$. We use the three-state approximation to the Ornstein–Uhlenbeck process, in which case we let the generator be
$\boldsymbol {u}_3(\boldsymbol {x}) = -\boldsymbol {u}(\boldsymbol {x})$. We use the three-state approximation to the Ornstein–Uhlenbeck process, in which case we let the generator be
 \begin{equation} \mathcal{Q} = \gamma \begin{bmatrix} -1 & 1/2 & 0 \\ 1 & -1 & 1 \\ 0 & 1/2 & -1 \end{bmatrix}, \end{equation}
\begin{equation} \mathcal{Q} = \gamma \begin{bmatrix} -1 & 1/2 & 0 \\ 1 & -1 & 1 \\ 0 & 1/2 & -1 \end{bmatrix}, \end{equation}
where ![]() $\gamma > 0$. This generator implies that the flow field stays in each state for an exponentially distributed amount of time, with each state's rate parameter
$\gamma > 0$. This generator implies that the flow field stays in each state for an exponentially distributed amount of time, with each state's rate parameter ![]() $\gamma$. Flow fields
$\gamma$. Flow fields ![]() $\boldsymbol {u}_1$ and
$\boldsymbol {u}_1$ and ![]() $\boldsymbol {u}_3$ always transition to state
$\boldsymbol {u}_3$ always transition to state ![]() $\boldsymbol {u}_2$ and
$\boldsymbol {u}_2$ and ![]() $\boldsymbol {u}_2$ transitions to either
$\boldsymbol {u}_2$ transitions to either ![]() $\boldsymbol {u}_1$ or
$\boldsymbol {u}_1$ or ![]() $\boldsymbol {u}_3$ with
$\boldsymbol {u}_3$ with ![]() $50\,\%$ probability. This stochastic process is a generalization of the model considered in the previous section and the class of problems considered by Ferrari et al. (Reference Ferrari, Manfroi and Young2001) since the flow field can have spatial structure and is not limited to one dimension.
$50\,\%$ probability. This stochastic process is a generalization of the model considered in the previous section and the class of problems considered by Ferrari et al. (Reference Ferrari, Manfroi and Young2001) since the flow field can have spatial structure and is not limited to one dimension.
The three-state system is viewed as a reduced-order statistical model for any flow field that randomly switches between clockwise or counterclockwise advection, such as the numerical and experimental flows of Sugiyama et al. (Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010). In their work, the numerical computations of 2-D Rayleigh–Bénard convection in a rectangular domain with no-slip boundary conditions along all walls yielded large-scale convection rolls that flipped orientation at random time intervals upon particular choices of Rayleigh and Prandtl numbers. In addition, they showed that the phenomenology could be observed in a laboratory experiment with a setup similar to that of Xia, Sun & Zhou (Reference Xia, Sun and Zhou2003). In general, we expect reducing the statistics of a flow to a continuous-time Markov process with discrete states to be useful and lead to tractable analysis in fluid flows characterized by distinct well-separated flow regimes with seemingly random transitions between behaviours. Consequently, a similar construction is possible for more complex three-dimensional flow fields, such as those of Brown & Ahlers (Reference Brown and Ahlers2007), or geophysical applications (Zhang, Zhang & Tian Reference Zhang, Zhang and Tian2022).
Proceeding with calculations, we note that the eigenvectors of the generator are
 \begin{equation} \boldsymbol{v}^1 = \begin{bmatrix} 1/4 \\ 1/2 \\ 1/4 \end{bmatrix},\quad \boldsymbol{v}^2 = \begin{bmatrix} 1/2 \\ 0 \\ -1/2 \end{bmatrix} \quad \text{and}\quad \boldsymbol{v}^3 = \begin{bmatrix} 1/4 \\ -1/2 \\ 1/4 \end{bmatrix} \end{equation}
\begin{equation} \boldsymbol{v}^1 = \begin{bmatrix} 1/4 \\ 1/2 \\ 1/4 \end{bmatrix},\quad \boldsymbol{v}^2 = \begin{bmatrix} 1/2 \\ 0 \\ -1/2 \end{bmatrix} \quad \text{and}\quad \boldsymbol{v}^3 = \begin{bmatrix} 1/4 \\ -1/2 \\ 1/4 \end{bmatrix} \end{equation}
with respective eigenvalues ![]() $\lambda ^1 = 0$,
$\lambda ^1 = 0$, ![]() $\lambda ^2 = - \gamma$ and
$\lambda ^2 = - \gamma$ and ![]() $\lambda ^3 = - 2 \gamma$.
$\lambda ^3 = - 2 \gamma$.
The statistically steady three-state manifestation of (2.13) and (2.14) is
We define a transformation using the eigenvectors of the generator ![]() $\mathcal {Q}$,
$\mathcal {Q}$,
 \begin{equation} \begin{bmatrix} 1/4 & 1/2 & 1/4 \\ 1/2 & 0 & -1/2 \\ 1/4 & -1/2 & 1/4 \end{bmatrix} \begin{bmatrix} \varphi_1 \\ \varphi_2 \\ \varphi_3 \end{bmatrix} = \begin{bmatrix} \varTheta_1 \\ \varTheta_2 \\ \varTheta_3 \end{bmatrix} \Leftrightarrow \begin{bmatrix} \varphi_1 \\ \varphi_2 \\ \varphi_3 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 \\ 1 & 0 & -1 \\ 1 & -1 & 1 \end{bmatrix} \begin{bmatrix} \varTheta_1 \\ \varTheta_2 \\ \varTheta_3 \end{bmatrix} \end{equation}
\begin{equation} \begin{bmatrix} 1/4 & 1/2 & 1/4 \\ 1/2 & 0 & -1/2 \\ 1/4 & -1/2 & 1/4 \end{bmatrix} \begin{bmatrix} \varphi_1 \\ \varphi_2 \\ \varphi_3 \end{bmatrix} = \begin{bmatrix} \varTheta_1 \\ \varTheta_2 \\ \varTheta_3 \end{bmatrix} \Leftrightarrow \begin{bmatrix} \varphi_1 \\ \varphi_2 \\ \varphi_3 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 \\ 1 & 0 & -1 \\ 1 & -1 & 1 \end{bmatrix} \begin{bmatrix} \varTheta_1 \\ \varTheta_2 \\ \varTheta_3 \end{bmatrix} \end{equation}resulting in the equations
We comment that ![]() $\varphi _1 = \langle \theta \rangle$, and that
$\varphi _1 = \langle \theta \rangle$, and that ![]() $\varphi _2$ and
$\varphi _2$ and ![]() $\varphi _3$ are thought of as perturbation variables. Furthermore, the turbulent flux is
$\varphi _3$ are thought of as perturbation variables. Furthermore, the turbulent flux is ![]() $\langle \boldsymbol {\tilde {u}}' \theta ' \rangle = \boldsymbol {u} \varphi _2$. We eliminate dependence on the perturbation variables
$\langle \boldsymbol {\tilde {u}}' \theta ' \rangle = \boldsymbol {u} \varphi _2$. We eliminate dependence on the perturbation variables ![]() $\varphi _2$ and
$\varphi _2$ and ![]() $\varphi _3$ by first solving for
$\varphi _3$ by first solving for ![]() $\varphi _3$ in terms of
$\varphi _3$ in terms of ![]() $\varphi _2$,
$\varphi _2$,
and then solving for ![]() $\varphi _2$ in terms of
$\varphi _2$ in terms of ![]() $\varphi _1$,
$\varphi _1$,
And finally, we write our equation for the ensemble mean as
from whence we extract the turbulent diffusivity operator
We point out a few salient features of (3.42).
For large ![]() $\kappa$, we have
$\kappa$, we have
The inverse Helmholtz operator, ![]() $(\gamma - \kappa \Delta )^{-1}$, damps high spatial frequency components of ensemble mean gradients. Thus, the operator's eigenvalues decrease as one examines increasingly fine-scale structure. Intuitively, as one examines a small-scale structure, the presence of diffusivity leads to lower turbulent fluxes, expressing that it is challenging to transport something that immediately diffuses.
$(\gamma - \kappa \Delta )^{-1}$, damps high spatial frequency components of ensemble mean gradients. Thus, the operator's eigenvalues decrease as one examines increasingly fine-scale structure. Intuitively, as one examines a small-scale structure, the presence of diffusivity leads to lower turbulent fluxes, expressing that it is challenging to transport something that immediately diffuses.
A second observation pertains to the presence of the eigenvalue of the generator in the operator. If the flow field changes rapidly, transitioning between the disparate states, then ![]() $\gamma$ is large and one can expect the turbulent diffusivity to be local. In other words, the flow does not stay sufficiently long time near a coherent structure. More concretely, larger transition rates correspond to an enhanced locality in the turbulent diffusivity operator since, as
$\gamma$ is large and one can expect the turbulent diffusivity to be local. In other words, the flow does not stay sufficiently long time near a coherent structure. More concretely, larger transition rates correspond to an enhanced locality in the turbulent diffusivity operator since, as ![]() $\gamma \rightarrow \infty$,
$\gamma \rightarrow \infty$,
Observe that (3.44) is the integrated autocorrelation of the stochastic flow field. Whether or not non-local effects matter depends on the characteristic time scale of the flow field, ![]() $L U^{-1}$ as well as the characteristic time scale for diffusion
$L U^{-1}$ as well as the characteristic time scale for diffusion ![]() $L^2 / \kappa$, as it compares to the characteristic time scale for transitioning between states,
$L^2 / \kappa$, as it compares to the characteristic time scale for transitioning between states, ![]() $\gamma ^{-1}$.
$\gamma ^{-1}$.
We see that the ![]() $\kappa \rightarrow 0$ limit retains a non-local feature since
$\kappa \rightarrow 0$ limit retains a non-local feature since
and the operator ![]() $(\boldsymbol {u}\boldsymbol {\cdot } \boldsymbol {\nabla })(\boldsymbol {u} \boldsymbol {\cdot } \boldsymbol {\nabla })$ can have a significant spatial structure. To further understand this point, we simplify by using the example from the previous section. Using the 1-D example in Fourier space and using the usual transcriptions
$(\boldsymbol {u}\boldsymbol {\cdot } \boldsymbol {\nabla })(\boldsymbol {u} \boldsymbol {\cdot } \boldsymbol {\nabla })$ can have a significant spatial structure. To further understand this point, we simplify by using the example from the previous section. Using the 1-D example in Fourier space and using the usual transcriptions ![]() $\Delta \rightarrow -k^2$,
$\Delta \rightarrow -k^2$, ![]() $\boldsymbol {\nabla } \rightarrow \iota k$, and with
$\boldsymbol {\nabla } \rightarrow \iota k$, and with ![]() $u > 0$, the kernel is
$u > 0$, the kernel is
 \begin{align} \dfrac{u^2}{2(\gamma + \kappa k^2) + \dfrac{u^2 k^2}{(\kappa k^2 + 2 \gamma)}} \rightarrow u \dfrac{ \dfrac{2 \gamma}{u} }{ \dfrac{4\gamma^2}{u^2} + k^2} \Rightarrow \mathcal{K}(x, x') = \dfrac{u}{2} \exp \left( -\dfrac{2 \gamma}{u} \left| x - x' \right| \right), \end{align}
\begin{align} \dfrac{u^2}{2(\gamma + \kappa k^2) + \dfrac{u^2 k^2}{(\kappa k^2 + 2 \gamma)}} \rightarrow u \dfrac{ \dfrac{2 \gamma}{u} }{ \dfrac{4\gamma^2}{u^2} + k^2} \Rightarrow \mathcal{K}(x, x') = \dfrac{u}{2} \exp \left( -\dfrac{2 \gamma}{u} \left| x - x' \right| \right), \end{align}
where in the last line, we used the inverse Fourier transform on the real line to simplify the structure of the kernel. (Accounting for finite domain effects yields the Fourier series of a hyperbolic cosine.) The left-most expression corresponds to the blue dots in figure 1 for ![]() $N=3$,
$N=3$, ![]() $u = \sqrt {2}$,
$u = \sqrt {2}$, ![]() $\gamma = 1$ and
$\gamma = 1$ and ![]() $\kappa = 0.01$ for each wavenumber
$\kappa = 0.01$ for each wavenumber ![]() $k \in \{0, 1, 2,\ldots, 7 \}$. In the right-most expression, we see the mean free path
$k \in \{0, 1, 2,\ldots, 7 \}$. In the right-most expression, we see the mean free path ![]() $\ell \equiv u / (2\gamma )$ as the characteristic width of the non-local kernel. Observe that by rescaling
$\ell \equiv u / (2\gamma )$ as the characteristic width of the non-local kernel. Observe that by rescaling ![]() $u \rightarrow \sqrt {2 \gamma } u$ and taking the limit as
$u \rightarrow \sqrt {2 \gamma } u$ and taking the limit as ![]() $\gamma \rightarrow \infty$ yields a delta function, a point that we come back to in § 4.3 and Appendix A. Furthermore, the weak velocity amplitude limit
$\gamma \rightarrow \infty$ yields a delta function, a point that we come back to in § 4.3 and Appendix A. Furthermore, the weak velocity amplitude limit ![]() $u \rightarrow 0$ is also local.
$u \rightarrow 0$ is also local.
To further explicate the conditional average procedure, we compare empirical conditional averages of (2.10) and (2.11) (specialized to the present system) to the direct conditionally averaged equations (3.36)–(3.38). Concretely, we use the flow field and source term
in a ![]() $2 {\rm \pi}$ periodic domain and
$2 {\rm \pi}$ periodic domain and ![]() $\gamma = 1$ for the transition rate. We employ a 2-D pseudo-spectral Fourier discretization with
$\gamma = 1$ for the transition rate. We employ a 2-D pseudo-spectral Fourier discretization with ![]() $48 \times 48$ grid points and evolve both systems to a time
$48 \times 48$ grid points and evolve both systems to a time ![]() $t=25$, which suffices for the flow and tracer to ‘forget’ its initial condition and reach a statistically steady state. For the stochastic differential equation, we use 10 000 ensemble members. We emphasize that the turbulent diffusivity operator is independent of the source term, and we make a choice for illustrative purposes.
$t=25$, which suffices for the flow and tracer to ‘forget’ its initial condition and reach a statistically steady state. For the stochastic differential equation, we use 10 000 ensemble members. We emphasize that the turbulent diffusivity operator is independent of the source term, and we make a choice for illustrative purposes.
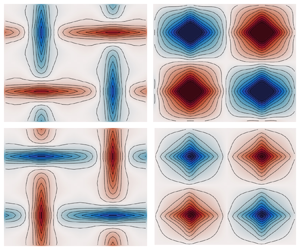
Figure 4 summarizes the result of comparing two different calculation methods. To compute the conditional averages, for example, ![]() $\varTheta _1$ at time
$\varTheta _1$ at time ![]() $t=25$, we proceed as follows. At the time
$t=25$, we proceed as follows. At the time ![]() $t=25$, we tag all fields that are currently being advected by
$t=25$, we tag all fields that are currently being advected by ![]() $\boldsymbol {u}_1$, add them up and then divide by the number of ensemble members, which in the present case is 10 000. This sequence of calculations yields
$\boldsymbol {u}_1$, add them up and then divide by the number of ensemble members, which in the present case is 10 000. This sequence of calculations yields ![]() $\varTheta _1$, shown in figure 4(a). The conditional means
$\varTheta _1$, shown in figure 4(a). The conditional means ![]() $\varTheta _2$ and
$\varTheta _2$ and ![]() $\varTheta _3$ are obtained similarly. We then calculate the conditional mean equations directly in the bottom row. All fields are plotted with respect to the same colour scale. For convenience, we also show the ensemble average, which here is
$\varTheta _3$ are obtained similarly. We then calculate the conditional mean equations directly in the bottom row. All fields are plotted with respect to the same colour scale. For convenience, we also show the ensemble average, which here is ![]() $\langle \theta \rangle = \varphi _1 = \varTheta _1 + \varTheta _2 + \varTheta _3$. The empirical averages have a slight asymmetry due to finite sampling effects. For reference, the source and stream function of the flow field are shown in the last column of the figure.
$\langle \theta \rangle = \varphi _1 = \varTheta _1 + \varTheta _2 + \varTheta _3$. The empirical averages have a slight asymmetry due to finite sampling effects. For reference, the source and stream function of the flow field are shown in the last column of the figure.

Figure 4. Three-state system. Here, we show the stream function, source term, conditional averages and the ensemble mean obtained using two different calculation methods. The first calculation method uses an empirical average with 10 000 ensemble members, and the second method uses the equations from the text. Both are shown at a final time of ![]() $T = 25$ time units where the statistical steady state has been reached.
$T = 25$ time units where the statistical steady state has been reached.
When the tracers are being advected by flow field ![]() $\boldsymbol {u}_1$, we see that the red in the stream function corresponds to a counterclockwise flow and the blue to a clockwise flow. The negative source concentration corresponding to the top left and bottom right parts of the domain are then transported vertically, whereas the positive source, located in the top right and bottom left of the domain, is transported horizontally. When advected by flow field
$\boldsymbol {u}_1$, we see that the red in the stream function corresponds to a counterclockwise flow and the blue to a clockwise flow. The negative source concentration corresponding to the top left and bottom right parts of the domain are then transported vertically, whereas the positive source, located in the top right and bottom left of the domain, is transported horizontally. When advected by flow field ![]() $\boldsymbol {u}_3$, the clockwise and counterclockwise roles reverse, and positive tracer sources are transported vertically and negative tracer sources are transported horizontally. When advected by
$\boldsymbol {u}_3$, the clockwise and counterclockwise roles reverse, and positive tracer sources are transported vertically and negative tracer sources are transported horizontally. When advected by ![]() $\boldsymbol {u}_2 = 0$, the conditional averages reflect the source term closely.
$\boldsymbol {u}_2 = 0$, the conditional averages reflect the source term closely.
Now that we have presented two examples, in the next section, we generalize by expressing the turbulent diffusivity operator in terms of the spectrum of the generator.
4. General approach
The previous example had the following pattern:
(i) compute the eigenvectors of the generator
 $\mathcal {Q}$;
$\mathcal {Q}$;(ii) transform the equations into a basis that diagonalizes
 $\mathcal {Q}$;
$\mathcal {Q}$;(iii) separate the mean equation from the perturbation equations;
(iv) solve for the perturbation variables in terms of the mean variable.
Here we aim to gather the above procedure in the general case where we have access to the eigenvectors of ![]() $\mathcal {Q}$. Furthermore, in the last example, we claimed that the local turbulent diffusivity approximation, as calculated by neglecting the effects of diffusion and perturbation gradients, is equivalent to calculating the integrated auto-correlation of the Markov process. We justify that claim in § 4.3.
$\mathcal {Q}$. Furthermore, in the last example, we claimed that the local turbulent diffusivity approximation, as calculated by neglecting the effects of diffusion and perturbation gradients, is equivalent to calculating the integrated auto-correlation of the Markov process. We justify that claim in § 4.3.
4.1. Notation
Let us establish a notation for the general procedure. We again let ![]() $\mathcal {Q}$ denote the generator with corresponding transition probability matrix
$\mathcal {Q}$ denote the generator with corresponding transition probability matrix ![]() $\mathscr {P}(\tau )$ given by the matrix exponential
$\mathscr {P}(\tau )$ given by the matrix exponential
The entries of the matrix ![]() $[\mathscr {P}(\tau )]_{mn}$ denote the transition probability of state
$[\mathscr {P}(\tau )]_{mn}$ denote the transition probability of state ![]() $n$ to the state
$n$ to the state ![]() $m$. In each column of the transition matrix, the sum of the entries is one. We assume a unique zero eigenvalue for
$m$. In each column of the transition matrix, the sum of the entries is one. We assume a unique zero eigenvalue for ![]() $\mathcal {Q}$ with all other eigenvalues negative. We also assume that the eigenvalues can be ordered in such a way that they are decreasing, i.e.
$\mathcal {Q}$ with all other eigenvalues negative. We also assume that the eigenvalues can be ordered in such a way that they are decreasing, i.e. ![]() $\lambda _1 = 0$,
$\lambda _1 = 0$, ![]() $\lambda _2 < 0$ and
$\lambda _2 < 0$ and ![]() $\lambda _i \leq \lambda _j$ for
$\lambda _i \leq \lambda _j$ for ![]() $i > j$ with
$i > j$ with ![]() $j \geq 2$. These choices result in a unique statistical steady state which we denote by the vector
$j \geq 2$. These choices result in a unique statistical steady state which we denote by the vector ![]() $\boldsymbol {v}_1$ with the property
$\boldsymbol {v}_1$ with the property
and similarly for the left eigenvector, ![]() $\boldsymbol {w}_1$. We denote the entries of
$\boldsymbol {w}_1$. We denote the entries of ![]() $\boldsymbol {v}_1$ and
$\boldsymbol {v}_1$ and ![]() $\boldsymbol {w}_1$ by column vectors
$\boldsymbol {w}_1$ by column vectors
 \begin{equation} \boldsymbol{v}_1 = \begin{bmatrix} P_1 \\ P_2 \\ \vdots \\ P_M \end{bmatrix} \quad \text{and}\quad \boldsymbol{w}_1 = \begin{bmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{bmatrix}, \end{equation}
\begin{equation} \boldsymbol{v}_1 = \begin{bmatrix} P_1 \\ P_2 \\ \vdots \\ P_M \end{bmatrix} \quad \text{and}\quad \boldsymbol{w}_1 = \begin{bmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{bmatrix}, \end{equation}
where ![]() $M$ is the number of states. We assume that the eigenvector
$M$ is the number of states. We assume that the eigenvector ![]() $\boldsymbol {v}_1$ is normalized such that
$\boldsymbol {v}_1$ is normalized such that ![]() $\sum _m P_m = 1$. Consequently,
$\sum _m P_m = 1$. Consequently, ![]() $\boldsymbol {w}_1 \boldsymbol {\cdot } \boldsymbol {v}_1 = \boldsymbol {w}_1^{\rm T} \boldsymbol {v}_1 = 1$. We introduce unit vectors
$\boldsymbol {w}_1 \boldsymbol {\cdot } \boldsymbol {v}_1 = \boldsymbol {w}_1^{\rm T} \boldsymbol {v}_1 = 1$. We introduce unit vectors ![]() $\hat {\boldsymbol {e}}_m$ whose
$\hat {\boldsymbol {e}}_m$ whose ![]() $m$th entry is zero and all other entries are zero, e.g.
$m$th entry is zero and all other entries are zero, e.g.
 \begin{equation} \hat{\boldsymbol{e}}_1 = \begin{bmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix} ,\quad \hat{\boldsymbol{e}}_2 = \begin{bmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{bmatrix} \quad \text{and}\quad \hat{\boldsymbol{e}}_M = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{bmatrix} . \end{equation}
\begin{equation} \hat{\boldsymbol{e}}_1 = \begin{bmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix} ,\quad \hat{\boldsymbol{e}}_2 = \begin{bmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{bmatrix} \quad \text{and}\quad \hat{\boldsymbol{e}}_M = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{bmatrix} . \end{equation}
Thus, ![]() $\boldsymbol {v}_1 = \sum _m P_m \boldsymbol {\hat {e}}_m$,
$\boldsymbol {v}_1 = \sum _m P_m \boldsymbol {\hat {e}}_m$, ![]() $\boldsymbol {w}_1 = \boldsymbol {\hat {e}}_m$. Furthermore,
$\boldsymbol {w}_1 = \boldsymbol {\hat {e}}_m$. Furthermore, ![]() $\boldsymbol {\hat {e}}_m \boldsymbol {\cdot } \boldsymbol {v}_1 = P_m$ and
$\boldsymbol {\hat {e}}_m \boldsymbol {\cdot } \boldsymbol {v}_1 = P_m$ and ![]() $\boldsymbol {\hat {e}}_m \boldsymbol {\cdot } \boldsymbol {w}_1 = 1$ for each
$\boldsymbol {\hat {e}}_m \boldsymbol {\cdot } \boldsymbol {w}_1 = 1$ for each ![]() $m$.
$m$.
For the discussion that follows, we will assume that the matrix ![]() $\mathcal {Q}$ has an eigenvalue decomposition. In general, we denote the right eigenvectors of
$\mathcal {Q}$ has an eigenvalue decomposition. In general, we denote the right eigenvectors of ![]() $\mathcal {Q}$ by
$\mathcal {Q}$ by ![]() $\boldsymbol {v}_i$ for
$\boldsymbol {v}_i$ for ![]() $i = 1, \ldots, M$ and the left eigenvectors by
$i = 1, \ldots, M$ and the left eigenvectors by ![]() $\boldsymbol {w}_i$ for
$\boldsymbol {w}_i$ for ![]() $i = 1,\ldots, M$. These vectors are all associated with eigenvalues
$i = 1,\ldots, M$. These vectors are all associated with eigenvalues ![]() $\lambda _i$ for
$\lambda _i$ for ![]() $i=1,\ldots, M$, where
$i=1,\ldots, M$, where ![]() $i=1$ denotes the unique eigenvalue
$i=1$ denotes the unique eigenvalue ![]() $\lambda _1 = 0$. We recall that the left eigenvectors can be constructed from the right eigenvectors by placing the right eigenvectors in the columns of a matrix
$\lambda _1 = 0$. We recall that the left eigenvectors can be constructed from the right eigenvectors by placing the right eigenvectors in the columns of a matrix ![]() $V$, computing the inverse
$V$, computing the inverse ![]() $V^{-1}$ and extracting the rows of the inverse. The aforementioned procedure guarantees the normalization
$V^{-1}$ and extracting the rows of the inverse. The aforementioned procedure guarantees the normalization ![]() $\boldsymbol {w}_j \boldsymbol {\cdot } \boldsymbol {v}_i = \boldsymbol {w}_i^{\rm T} \boldsymbol {v}_j = \delta _{ij}$. Thus, we have the relations
$\boldsymbol {w}_j \boldsymbol {\cdot } \boldsymbol {v}_i = \boldsymbol {w}_i^{\rm T} \boldsymbol {v}_j = \delta _{ij}$. Thus, we have the relations
With notation now in place, we observe that the operators ![]() $\mathcal {Q}$ and
$\mathcal {Q}$ and ![]() $\mathscr {P}(\tau )$ are characterized by their spectral decomposition
$\mathscr {P}(\tau )$ are characterized by their spectral decomposition
We now introduce our Markov states as steady vector fields. The use of several vector spaces imposes a burden on notation: the vector spaces associated with Markov states, ensemble members and the vector field ![]() $\boldsymbol {u}$. Instead of using overly decorated notation with an excessive number of indices, we introduce the convention that
$\boldsymbol {u}$. Instead of using overly decorated notation with an excessive number of indices, we introduce the convention that ![]() $\boldsymbol {u}$ will always belong to the vector space associated with the vector field, and all other vectors are associated with the vector space of Markov states. For example, if we have two flow states
$\boldsymbol {u}$ will always belong to the vector space associated with the vector field, and all other vectors are associated with the vector space of Markov states. For example, if we have two flow states ![]() $\boldsymbol {u}_1$ and
$\boldsymbol {u}_1$ and ![]() $\boldsymbol {u}_2$, then
$\boldsymbol {u}_2$, then
4.2. Spectral representation
With this notation now in place, the statistically steady equations
are represented as the matrix system
 \begin{equation} \sum_{m} \hat{\boldsymbol{e}}_m \boldsymbol{\nabla} \boldsymbol{\cdot} \left( \boldsymbol{u}_m \varTheta_m \right)= \sum_{m} \hat{\boldsymbol{e}}_m \kappa \Delta \varTheta_m + s \boldsymbol{v}_1 + \mathcal{Q} \left(\sum_{m} \hat{\boldsymbol{e}}_m \varTheta_m \right), \end{equation}
\begin{equation} \sum_{m} \hat{\boldsymbol{e}}_m \boldsymbol{\nabla} \boldsymbol{\cdot} \left( \boldsymbol{u}_m \varTheta_m \right)= \sum_{m} \hat{\boldsymbol{e}}_m \kappa \Delta \varTheta_m + s \boldsymbol{v}_1 + \mathcal{Q} \left(\sum_{m} \hat{\boldsymbol{e}}_m \varTheta_m \right), \end{equation}
where we made use of ![]() $\sum _m \boldsymbol {\hat {e}}_m P_m = \boldsymbol {v}_1$. We now re-express (4.10) in terms of a basis that uses the eigenvectors of the transition matrix. Define components
$\sum _m \boldsymbol {\hat {e}}_m P_m = \boldsymbol {v}_1$. We now re-express (4.10) in terms of a basis that uses the eigenvectors of the transition matrix. Define components ![]() $\varphi _n$ by the change of basis formula
$\varphi _n$ by the change of basis formula
We make the observation ![]() $\varphi _1 = \langle \theta \rangle$. We have the following relations based on the general definitions of the left eigenvectors
$\varphi _1 = \langle \theta \rangle$. We have the following relations based on the general definitions of the left eigenvectors ![]() $\boldsymbol {w}_n$ and right eigenvectors
$\boldsymbol {w}_n$ and right eigenvectors ![]() $\boldsymbol {v}_n$,
$\boldsymbol {v}_n$,
Multiplying (4.10) by ![]() $\boldsymbol {w}^{\rm T}_j$ and making use of (4.12a,b), we get
$\boldsymbol {w}^{\rm T}_j$ and making use of (4.12a,b), we get
 \begin{align} \sum_{n} (\boldsymbol{w}_j \boldsymbol{\cdot} \hat{\boldsymbol{e}}_n) \boldsymbol{\nabla} \boldsymbol{\cdot} \left( \boldsymbol{u}_n \varTheta_n \right) &= \kappa \Delta \varphi_j + \delta_{1j} s + \lambda_j \varphi_j\\ &\Rightarrow\nonumber \end{align}
\begin{align} \sum_{n} (\boldsymbol{w}_j \boldsymbol{\cdot} \hat{\boldsymbol{e}}_n) \boldsymbol{\nabla} \boldsymbol{\cdot} \left( \boldsymbol{u}_n \varTheta_n \right) &= \kappa \Delta \varphi_j + \delta_{1j} s + \lambda_j \varphi_j\\ &\Rightarrow\nonumber \end{align} \begin{align} \sum_{n} (\boldsymbol{w}_j \boldsymbol{\cdot} \hat{\boldsymbol{e}}_n) \boldsymbol{\nabla} \boldsymbol{\cdot} \left( \boldsymbol{u}_n \left[ \sum_i \boldsymbol{\hat{e}}_n \boldsymbol{\cdot} \boldsymbol{v}_i \varphi_i \right] \right) &= \kappa \Delta \varphi_j + \delta_{1j} s + \lambda_j \varphi_j\\ &\Rightarrow\nonumber \end{align}
\begin{align} \sum_{n} (\boldsymbol{w}_j \boldsymbol{\cdot} \hat{\boldsymbol{e}}_n) \boldsymbol{\nabla} \boldsymbol{\cdot} \left( \boldsymbol{u}_n \left[ \sum_i \boldsymbol{\hat{e}}_n \boldsymbol{\cdot} \boldsymbol{v}_i \varphi_i \right] \right) &= \kappa \Delta \varphi_j + \delta_{1j} s + \lambda_j \varphi_j\\ &\Rightarrow\nonumber \end{align}
We now wish to decompose (4.14) into a mean equation, index ![]() $j=1$, and perturbation equations,
$j=1$, and perturbation equations, ![]() $j>1$. For the mean equation, index
$j>1$. For the mean equation, index ![]() $j = 1$, we make use of the properties
$j = 1$, we make use of the properties
to arrive at (after changing summation index from ![]() $n$ to
$n$ to ![]() $m$)
$m$)
 \begin{equation} \boldsymbol{\nabla} \boldsymbol{\cdot} \left( \langle \boldsymbol{u} \rangle \varphi_1 \right) + \boldsymbol{\nabla} \boldsymbol{\cdot} \left[ \sum_{(i\neq 1) m} (\boldsymbol{\hat{e}}_m \boldsymbol{\cdot} \boldsymbol{v}_i ) \boldsymbol{u}_m \varphi_i \right] = \kappa \Delta \varphi_1 + s. \end{equation}
\begin{equation} \boldsymbol{\nabla} \boldsymbol{\cdot} \left( \langle \boldsymbol{u} \rangle \varphi_1 \right) + \boldsymbol{\nabla} \boldsymbol{\cdot} \left[ \sum_{(i\neq 1) m} (\boldsymbol{\hat{e}}_m \boldsymbol{\cdot} \boldsymbol{v}_i ) \boldsymbol{u}_m \varphi_i \right] = \kappa \Delta \varphi_1 + s. \end{equation}We make the observation that the turbulent flux is
and comment that the flow fields ![]() $\boldsymbol {U}_i(\boldsymbol {x}) \equiv \sum _{m} (\boldsymbol {\hat {e}}_m \boldsymbol {\cdot } \boldsymbol {v}_i ) \boldsymbol {u}_m$ are the Koopman mode amplitudes associated with eigenvalue
$\boldsymbol {U}_i(\boldsymbol {x}) \equiv \sum _{m} (\boldsymbol {\hat {e}}_m \boldsymbol {\cdot } \boldsymbol {v}_i ) \boldsymbol {u}_m$ are the Koopman mode amplitudes associated with eigenvalue ![]() $\lambda _i$. These are the relevant statistical spatial structures that advect the statistical perturbation variables
$\lambda _i$. These are the relevant statistical spatial structures that advect the statistical perturbation variables ![]() $\varphi _i$. This is similar to how the ensemble mean flow field advects the ensemble mean tracer concentration. Stated differently, the perturbation variables are advected by structures associated with non-trivial Koopman modes.
$\varphi _i$. This is similar to how the ensemble mean flow field advects the ensemble mean tracer concentration. Stated differently, the perturbation variables are advected by structures associated with non-trivial Koopman modes.
The perturbation equations, indices ![]() $j > 1$, are
$j > 1$, are
We isolate the dependence on the mean gradients by rearranging the above expression as follows for ![]() $j > 1$:
$j > 1$:
where we used ![]() $\boldsymbol {\hat {e}}_n \boldsymbol {\cdot } \boldsymbol {v}_1 = P_n$. Assuming that the operator on the left-hand side of (4.20) is invertible, we introduce the Green's function,
$\boldsymbol {\hat {e}}_n \boldsymbol {\cdot } \boldsymbol {v}_1 = P_n$. Assuming that the operator on the left-hand side of (4.20) is invertible, we introduce the Green's function, ![]() $\mathcal {G}_{ij}$, to yield
$\mathcal {G}_{ij}$, to yield
 \begin{equation} \varphi_i ={-} \int \,{\rm d} \boldsymbol{x}' \sum_{(\,j{\neq}1) n} \mathcal{G}_{ij}(\boldsymbol{x} | \boldsymbol{x}') P_n (\boldsymbol{w}_j \boldsymbol{\cdot} \hat{\boldsymbol{e}}_n) \boldsymbol{\nabla}_{\boldsymbol{x}'} \boldsymbol{\cdot} \left( \boldsymbol{u}_n(\boldsymbol{x}') \varphi_1(\boldsymbol{x}') \right) \quad\text{for } i \neq 1. \end{equation}
\begin{equation} \varphi_i ={-} \int \,{\rm d} \boldsymbol{x}' \sum_{(\,j{\neq}1) n} \mathcal{G}_{ij}(\boldsymbol{x} | \boldsymbol{x}') P_n (\boldsymbol{w}_j \boldsymbol{\cdot} \hat{\boldsymbol{e}}_n) \boldsymbol{\nabla}_{\boldsymbol{x}'} \boldsymbol{\cdot} \left( \boldsymbol{u}_n(\boldsymbol{x}') \varphi_1(\boldsymbol{x}') \right) \quad\text{for } i \neq 1. \end{equation}Thus, we represent our turbulent flux as
 \begin{align} \langle \boldsymbol{ \tilde{u} }' \theta' \rangle ={-} \int \,{\rm d} \boldsymbol{x}' \sum_{(i\neq 1)(\,j {\neq} 1) m n } (\boldsymbol{\hat{e}}_m \boldsymbol{\cdot} \boldsymbol{v}_i ) \boldsymbol{u}_m (\boldsymbol{x}) \mathcal{G}_{ij}(\boldsymbol{x} | \boldsymbol{x}') P_n (\boldsymbol{w}_j \boldsymbol{\cdot} \hat{\boldsymbol{e}}_n) \boldsymbol{\nabla}_{\boldsymbol{x}'} \boldsymbol{\cdot} \left( \boldsymbol{u}_n(\boldsymbol{x}') \varphi_1(\boldsymbol{x}') \right) . \end{align}
\begin{align} \langle \boldsymbol{ \tilde{u} }' \theta' \rangle ={-} \int \,{\rm d} \boldsymbol{x}' \sum_{(i\neq 1)(\,j {\neq} 1) m n } (\boldsymbol{\hat{e}}_m \boldsymbol{\cdot} \boldsymbol{v}_i ) \boldsymbol{u}_m (\boldsymbol{x}) \mathcal{G}_{ij}(\boldsymbol{x} | \boldsymbol{x}') P_n (\boldsymbol{w}_j \boldsymbol{\cdot} \hat{\boldsymbol{e}}_n) \boldsymbol{\nabla}_{\boldsymbol{x}'} \boldsymbol{\cdot} \left( \boldsymbol{u}_n(\boldsymbol{x}') \varphi_1(\boldsymbol{x}') \right) . \end{align}For compressible flow, the eddy-flux depends on both the ensemble mean gradients and the ensemble mean value; otherwise, when each Markov state is incompressible,
 \begin{equation} \langle \boldsymbol{ \tilde{u} }' \theta' \rangle ={-} \int \,{\rm d} \boldsymbol{x}' \sum_{(i\neq 1)(\,j {\neq}1) m n } (\boldsymbol{\hat{e}}_m \boldsymbol{\cdot} \boldsymbol{v}_i ) \boldsymbol{u}_m (\boldsymbol{x}) \mathcal{G}_{ij}(\boldsymbol{x} | \boldsymbol{x}') P_n (\boldsymbol{w}_j \boldsymbol{\cdot} \hat{\boldsymbol{e}}_n) \boldsymbol{u}_n(\boldsymbol{x}') \boldsymbol{\cdot} \boldsymbol{\nabla}_{\boldsymbol{x}'} \varphi_1(\boldsymbol{x}'), \end{equation}
\begin{equation} \langle \boldsymbol{ \tilde{u} }' \theta' \rangle ={-} \int \,{\rm d} \boldsymbol{x}' \sum_{(i\neq 1)(\,j {\neq}1) m n } (\boldsymbol{\hat{e}}_m \boldsymbol{\cdot} \boldsymbol{v}_i ) \boldsymbol{u}_m (\boldsymbol{x}) \mathcal{G}_{ij}(\boldsymbol{x} | \boldsymbol{x}') P_n (\boldsymbol{w}_j \boldsymbol{\cdot} \hat{\boldsymbol{e}}_n) \boldsymbol{u}_n(\boldsymbol{x}') \boldsymbol{\cdot} \boldsymbol{\nabla}_{\boldsymbol{x}'} \varphi_1(\boldsymbol{x}'), \end{equation}in which case the turbulent diffusivity kernel is
The above expression completes the procedure that we enacted for the examples in § 3.
We now discuss local approximations to the turbulent diffusivity operator.
4.3. Local approximation
We start with the same local diffusivity approximation of § 3.2 but using the spectral representation of (2.13) and (2.14). In the perturbation equations, neglect the dissipation operator and perturbation gradients, e.g. only include index ![]() $i=1$, to yield the following reduction of (4.19),
$i=1$, to yield the following reduction of (4.19),
where we used ![]() $(\boldsymbol {\hat {e}}_n \boldsymbol {\cdot } \boldsymbol {v}_1 ) = P_n$ and have changed indices from
$(\boldsymbol {\hat {e}}_n \boldsymbol {\cdot } \boldsymbol {v}_1 ) = P_n$ and have changed indices from ![]() $j$ to
$j$ to ![]() $i$. We solve for
$i$. We solve for ![]() $\varphi _i$ for
$\varphi _i$ for ![]() $i > 1$ and focus on the perturbation flux term in (4.17),
$i > 1$ and focus on the perturbation flux term in (4.17),
to get the local turbulent diffusivity estimate,
 \begin{align} \sum_{(i\neq 1) m} (\boldsymbol{\hat{e}}_m \boldsymbol{\cdot} \boldsymbol{v}_i ) \boldsymbol{u}_m \varphi_i &= \sum_{(i\neq 1) m} (\boldsymbol{\hat{e}}_m \boldsymbol{\cdot} \boldsymbol{v}_i ) \boldsymbol{u}_m \left[\frac{1}{\lambda_i} \sum_{n} (\boldsymbol{w}_i \boldsymbol{\cdot} \hat{\boldsymbol{e}}_n) P_n \left( \boldsymbol{u}_n \boldsymbol{\cdot} \boldsymbol{\nabla} \varphi_1 \right) \right] \end{align}
\begin{align} \sum_{(i\neq 1) m} (\boldsymbol{\hat{e}}_m \boldsymbol{\cdot} \boldsymbol{v}_i ) \boldsymbol{u}_m \varphi_i &= \sum_{(i\neq 1) m} (\boldsymbol{\hat{e}}_m \boldsymbol{\cdot} \boldsymbol{v}_i ) \boldsymbol{u}_m \left[\frac{1}{\lambda_i} \sum_{n} (\boldsymbol{w}_i \boldsymbol{\cdot} \hat{\boldsymbol{e}}_n) P_n \left( \boldsymbol{u}_n \boldsymbol{\cdot} \boldsymbol{\nabla} \varphi_1 \right) \right] \end{align} \begin{align} &= \underbrace{\left[ \sum_{(i \neq 1)mn} \frac{-1}{\lambda_i} ( \boldsymbol{\hat{e}}_m \boldsymbol{\cdot} \boldsymbol{v}_i ) (\boldsymbol{w}_i \boldsymbol{\cdot} \boldsymbol{\hat{e}}_n) \boldsymbol{u}_m \otimes P_n \boldsymbol{u}_n \right]}_{\boldsymbol{D}} \boldsymbol{\cdot} (- \boldsymbol{\nabla} \varphi_1) . \end{align}
\begin{align} &= \underbrace{\left[ \sum_{(i \neq 1)mn} \frac{-1}{\lambda_i} ( \boldsymbol{\hat{e}}_m \boldsymbol{\cdot} \boldsymbol{v}_i ) (\boldsymbol{w}_i \boldsymbol{\cdot} \boldsymbol{\hat{e}}_n) \boldsymbol{u}_m \otimes P_n \boldsymbol{u}_n \right]}_{\boldsymbol{D}} \boldsymbol{\cdot} (- \boldsymbol{\nabla} \varphi_1) . \end{align}We aim to show that the turbulent diffusivity from (4.28),
 \begin{equation} \boldsymbol{D} = \sum_{(i \neq 1)mn} \frac{-1}{\lambda_i} ( \boldsymbol{\hat{e}}_m \boldsymbol{\cdot} \boldsymbol{v}_i ) (\boldsymbol{w}_i \boldsymbol{\cdot} \boldsymbol{\hat{e}}_n) \boldsymbol{u}_m \otimes P_n \boldsymbol{u}_n, \end{equation}
\begin{equation} \boldsymbol{D} = \sum_{(i \neq 1)mn} \frac{-1}{\lambda_i} ( \boldsymbol{\hat{e}}_m \boldsymbol{\cdot} \boldsymbol{v}_i ) (\boldsymbol{w}_i \boldsymbol{\cdot} \boldsymbol{\hat{e}}_n) \boldsymbol{u}_m \otimes P_n \boldsymbol{u}_n, \end{equation}is equivalent to estimating the diffusivity by calculating the integral of the velocity perturbation autocorrelation in a statistically steady state,
The above turbulent diffusivity is expected to work well in the limit that diffusive effects can be neglected and the velocity field transitions rapidly with respect to the advective time scale, see Appendix A. Under such circumstances, it is not unreasonable to think of velocity fluctuations as analogous to white noise with a given covariance structure. For example, letting ![]() $\boldsymbol {\xi }$ be a white-noise process and
$\boldsymbol {\xi }$ be a white-noise process and ![]() $\boldsymbol {\sigma }$ be a variance vector, if
$\boldsymbol {\sigma }$ be a variance vector, if
then a diffusivity is given by
Indeed, we will show that the intuitive estimate,
does correspond to (4.29). Using the white-noise limit, one can take the advection term in the tracer equation as a state-dependent noise term, in the Stratonovich sense, from whence standard arguments follow. However, the current approach goes beyond this limit by allowing for temporal correlations of the flow field.
We begin with two observations. First, the statistically steady velocity field satisfies
where ![]() $\boldsymbol {u}_m(\boldsymbol {x})$ for each
$\boldsymbol {u}_m(\boldsymbol {x})$ for each ![]() $m$ are the states of the Markov process. Second, recall that the vector
$m$ are the states of the Markov process. Second, recall that the vector ![]() $\mathscr {P}(\tau ) \boldsymbol {\hat {e}}_n$ is a column vector of probabilities whose entries denote the probability of being found in state
$\mathscr {P}(\tau ) \boldsymbol {\hat {e}}_n$ is a column vector of probabilities whose entries denote the probability of being found in state ![]() $m$ given that at time
$m$ given that at time ![]() $\tau = 0$, the probability of being found in state
$\tau = 0$, the probability of being found in state ![]() $n$ is one. Thus, the conditional expectation of
$n$ is one. Thus, the conditional expectation of ![]() $\boldsymbol {u}(\boldsymbol {x}, t + \tau )$ given
$\boldsymbol {u}(\boldsymbol {x}, t + \tau )$ given ![]() $\boldsymbol {u}(\boldsymbol {x}, t ) = \boldsymbol {u}_n(\boldsymbol {x})$ is
$\boldsymbol {u}(\boldsymbol {x}, t ) = \boldsymbol {u}_n(\boldsymbol {x})$ is
 \begin{align} \langle \boldsymbol{\tilde{u}}(\boldsymbol{x}, t + \tau ) \rangle_{\boldsymbol{\tilde{u}}(\boldsymbol{x}, t ) = \boldsymbol{u}_n(\boldsymbol{x}) } &= \left(\sum_m \boldsymbol{u}_m (\boldsymbol{x}) \hat{\boldsymbol{e}}_m \right)^{\rm T} \mathscr{P}(\tau) \boldsymbol{\hat{e}}_n \end{align}
\begin{align} \langle \boldsymbol{\tilde{u}}(\boldsymbol{x}, t + \tau ) \rangle_{\boldsymbol{\tilde{u}}(\boldsymbol{x}, t ) = \boldsymbol{u}_n(\boldsymbol{x}) } &= \left(\sum_m \boldsymbol{u}_m (\boldsymbol{x}) \hat{\boldsymbol{e}}_m \right)^{\rm T} \mathscr{P}(\tau) \boldsymbol{\hat{e}}_n \end{align}
Equation (4.35) expresses the conditional expectation as a weighted sum of Markov states ![]() $\boldsymbol {u}_m(\boldsymbol {x})$.
$\boldsymbol {u}_m(\boldsymbol {x})$.
We are now in a position to characterize the local turbulent diffusivity estimate. The local turbulent diffusivity is computed by taking the long time integral of a statistically steady flow field's autocorrelation function, i.e.
where
We calculate the second term under the statistically steady assumption of (4.38),
 \begin{equation} \langle \boldsymbol{\tilde{u}}(\boldsymbol{x}, t + \tau) \rangle \otimes \langle \boldsymbol{\tilde{u}}(\boldsymbol{x}, t) \rangle = \left( \sum_m P_m \boldsymbol{u}_m(\boldsymbol{x} ) \right) \otimes \left( \sum_n P_n \boldsymbol{u}_n(\boldsymbol{x} ) \right) . \end{equation}
\begin{equation} \langle \boldsymbol{\tilde{u}}(\boldsymbol{x}, t + \tau) \rangle \otimes \langle \boldsymbol{\tilde{u}}(\boldsymbol{x}, t) \rangle = \left( \sum_m P_m \boldsymbol{u}_m(\boldsymbol{x} ) \right) \otimes \left( \sum_n P_n \boldsymbol{u}_n(\boldsymbol{x} ) \right) . \end{equation}For the first term of (4.38), we decompose the expectation into conditional expectations,
Given that we are in a statistically steady state, we use (4.35) to establish
We isolate the ![]() $i=1$ index and use
$i=1$ index and use ![]() $\lambda _1 = 0$,
$\lambda _1 = 0$, ![]() $\boldsymbol {\hat {e}}_m \boldsymbol {\cdot } \boldsymbol {v}_1 = P_m$, and
$\boldsymbol {\hat {e}}_m \boldsymbol {\cdot } \boldsymbol {v}_1 = P_m$, and ![]() $\boldsymbol {w}_1 \boldsymbol {\cdot } \boldsymbol {\hat {e}}_n = 1$ to arrive at
$\boldsymbol {w}_1 \boldsymbol {\cdot } \boldsymbol {\hat {e}}_n = 1$ to arrive at
 \begin{equation} \sum_{mn} {\rm e}^{\tau \lambda_1} ( \boldsymbol{\hat{e}}_m \boldsymbol{\cdot} \boldsymbol{v}_1 ) (\boldsymbol{w}_1 \boldsymbol{\cdot} \boldsymbol{\hat{e}}_n) \boldsymbol{u}_m \otimes P_n \boldsymbol{u}_n = \left(\sum_m P_m \boldsymbol{u}_m \right) \otimes \left(\sum_n P_n \boldsymbol{u}_n \right) . \end{equation}
\begin{equation} \sum_{mn} {\rm e}^{\tau \lambda_1} ( \boldsymbol{\hat{e}}_m \boldsymbol{\cdot} \boldsymbol{v}_1 ) (\boldsymbol{w}_1 \boldsymbol{\cdot} \boldsymbol{\hat{e}}_n) \boldsymbol{u}_m \otimes P_n \boldsymbol{u}_n = \left(\sum_m P_m \boldsymbol{u}_m \right) \otimes \left(\sum_n P_n \boldsymbol{u}_n \right) . \end{equation}Equation (4.43) cancels with (4.39) so that in total, we have the following characterization of (4.38):
Equation (4.44) is integrated to yield the local turbulent diffusivity,
 \begin{equation} \boldsymbol{D}(\boldsymbol{x}) = \int_0^\infty \boldsymbol{R}(\boldsymbol{x}, \tau) \,{\rm d} \tau = \sum_{(i \neq 1)mn} \frac{-1}{\lambda_i} ( \boldsymbol{\hat{e}}_m \boldsymbol{\cdot} \boldsymbol{v}_i ) (\boldsymbol{w}_i \boldsymbol{\cdot} \boldsymbol{\hat{e}}_n) \boldsymbol{u}_m \otimes P_n \boldsymbol{u}_n, \end{equation}
\begin{equation} \boldsymbol{D}(\boldsymbol{x}) = \int_0^\infty \boldsymbol{R}(\boldsymbol{x}, \tau) \,{\rm d} \tau = \sum_{(i \neq 1)mn} \frac{-1}{\lambda_i} ( \boldsymbol{\hat{e}}_m \boldsymbol{\cdot} \boldsymbol{v}_i ) (\boldsymbol{w}_i \boldsymbol{\cdot} \boldsymbol{\hat{e}}_n) \boldsymbol{u}_m \otimes P_n \boldsymbol{u}_n, \end{equation}
where we used ![]() $\lambda _i < 0$ for
$\lambda _i < 0$ for ![]() $i > 1$. A comparison of (4.45) and (4.29) reveals the correspondence. The expression on the right-hand side is related to the negative of the Moore–Penrose inverse of generator
$i > 1$. A comparison of (4.45) and (4.29) reveals the correspondence. The expression on the right-hand side is related to the negative of the Moore–Penrose inverse of generator ![]() $Q$. Thus, we see that estimating the diffusivity through the velocity autocorrelation integral is equivalent to neglecting diffusive effects and perturbation gradients. We further justify the local approximation as an asymptotic ‘white-noise’ limit and show to how connect the present class of stochastic models to that of Kraichnan (Reference Kraichnan1968) in Appendix A.
$Q$. Thus, we see that estimating the diffusivity through the velocity autocorrelation integral is equivalent to neglecting diffusive effects and perturbation gradients. We further justify the local approximation as an asymptotic ‘white-noise’ limit and show to how connect the present class of stochastic models to that of Kraichnan (Reference Kraichnan1968) in Appendix A.
5. Advanced example: stochastic wave in a channel
Now that we have outlined the general theory, we apply it to a wandering wave in a channel. The application is motivated by Flierl & McGillicuddy (Reference Flierl and McGillicuddy2002), where the wave in question is considered a Rossby wave. Consider the 2-D vorticity equation in a channel
with a stochastic forcing ![]() $f_{\omega }$ and
$f_{\omega }$ and ![]() $\{a, b\} = - \partial _y a \partial _x b + \partial _x a \partial _y b$. Here,
$\{a, b\} = - \partial _y a \partial _x b + \partial _x a \partial _y b$. Here, ![]() $x \in [0, 2{\rm \pi} )$ is periodic and
$x \in [0, 2{\rm \pi} )$ is periodic and ![]() $y \in [0, 1]$ is wall bounded. No-flux boundary conditions for the tracer and stress-free boundary conditions for the flow field on the wall
$y \in [0, 1]$ is wall bounded. No-flux boundary conditions for the tracer and stress-free boundary conditions for the flow field on the wall ![]() $y=0, 1$ are imposed. A solution to the vorticity equation is
$y=0, 1$ are imposed. A solution to the vorticity equation is
upon choosing
The nonlinear term in the vorticity equation is zero since ![]() $\psi _{\omega } \propto q_{\omega }$, i.e.
$\psi _{\omega } \propto q_{\omega }$, i.e. ![]() $\{ \psi _{\omega }, q_{\omega } \} = 0$. The phase
$\{ \psi _{\omega }, q_{\omega } \} = 0$. The phase ![]() $\varphi$ is a random walk with drift
$\varphi$ is a random walk with drift ![]() $c$ in a
$c$ in a ![]() $2{\rm \pi}$ periodic domain. The wave propagates, on average, to the left. For simulation purposes, we choose
$2{\rm \pi}$ periodic domain. The wave propagates, on average, to the left. For simulation purposes, we choose ![]() $c = \epsilon = 1$ and
$c = \epsilon = 1$ and ![]() $\kappa = 0.01$.
$\kappa = 0.01$.
The conditional mean equations for the passive tracer are
where ![]() $\varTheta = \varTheta (\boldsymbol {x}, \varphi, t)$ and
$\varTheta = \varTheta (\boldsymbol {x}, \varphi, t)$ and ![]() $\psi = \sin ( x + \varphi ) \sin ( {\rm \pi}y )$ with
$\psi = \sin ( x + \varphi ) \sin ( {\rm \pi}y )$ with ![]() $\varphi \in [0, 2 {\rm \pi})$. Discretizing the phase variable
$\varphi \in [0, 2 {\rm \pi})$. Discretizing the phase variable ![]() $\varphi$ with a finite volume method in
$\varphi$ with a finite volume method in ![]() $\varphi$ yields
$\varphi$ yields
where the details of the ![]() $Q_{m m'}$ and
$Q_{m m'}$ and ![]() $\psi _m$ are given in Appendix C.3. Discretizing with a spectral method for
$\psi _m$ are given in Appendix C.3. Discretizing with a spectral method for ![]() $\varphi$ yields faster convergence to the continuous problem. However, the finite-volume discretization yields sequences of realizable stochastic processes in the form of a Markov jump process between different flow fields.
$\varphi$ yields faster convergence to the continuous problem. However, the finite-volume discretization yields sequences of realizable stochastic processes in the form of a Markov jump process between different flow fields.
For a local diffusivity, we use the auto-correlation of the velocity field,
and calculate an approximate evolution equation
We numerically solve both (5.1), the conditional mean equation (5.9) for increasing number of states, and the local diffusivity equation, (5.11), for the particular choice of source term,
which is shown in figure 5(c). We use a doubly periodic Fourier code with ![]() $N=32$ grid points in a domain
$N=32$ grid points in a domain ![]() $x \in [0, 2{\rm \pi} )$ and
$x \in [0, 2{\rm \pi} )$ and ![]() $y\in [0, 2)$, and note that no-flux and stress-free boundary conditions at
$y\in [0, 2)$, and note that no-flux and stress-free boundary conditions at ![]() $y=0$ and
$y=0$ and ![]() $y=1$ are satisfied. We evolve all solutions to a final time
$y=1$ are satisfied. We evolve all solutions to a final time ![]() $t=10$ and use 10 000 ensemble members for the stochastic evolution of the equations. We choose to show the effect of the turbulent diffusivity indirectly via the choice of source term and the ensemble mean rather than directly examining the structure of the exact non-local tensor kernel for the present circumstance.
$t=10$ and use 10 000 ensemble members for the stochastic evolution of the equations. We choose to show the effect of the turbulent diffusivity indirectly via the choice of source term and the ensemble mean rather than directly examining the structure of the exact non-local tensor kernel for the present circumstance.

Figure 5. Ensemble mean channel comparison. We show the ensemble mean of the wandering wave as compared to the six-state system and a local diffusivity estimate. For reference, we also show the source term, scaled by a factor of ![]() $0.1$ so as to be the same scale as the ensemble mean. A six-state system is visually similar to the continuous empirical mean, and the local diffusivity estimate is dissimilar.
$0.1$ so as to be the same scale as the ensemble mean. A six-state system is visually similar to the continuous empirical mean, and the local diffusivity estimate is dissimilar.
In addition, we show the ensemble mean of a six-state approximation to the kernel in figure 5(a), the empirical ensemble mean in figure 5(b) and the local diffusivity tensor results in figure 5(d). In the ![]() $x \in [4, 5]$ region of the plot, we see that the shape of the empirical ensemble mean is well captured by both the six-state approximation to the ensemble mean as well as the local diffusivity estimate; however, the magnitude is underestimated by the local diffusivity tensor. Furthermore, the local diffusivity tensor fails to capture the structure and magnitude of the ensemble mean in the
$x \in [4, 5]$ region of the plot, we see that the shape of the empirical ensemble mean is well captured by both the six-state approximation to the ensemble mean as well as the local diffusivity estimate; however, the magnitude is underestimated by the local diffusivity tensor. Furthermore, the local diffusivity tensor fails to capture the structure and magnitude of the ensemble mean in the ![]() $x \in [0, 3]$. In contrast, the
$x \in [0, 3]$. In contrast, the ![]() $N=6$ state approximation captures the structure and magnitude throughout the domain.
$N=6$ state approximation captures the structure and magnitude throughout the domain.
We quantify these statements with a relative ![]() $L^2$ error metric in figure 6. The sampling error is estimated by computing the difference in the empirical ensemble mean between ensemble members
$L^2$ error metric in figure 6. The sampling error is estimated by computing the difference in the empirical ensemble mean between ensemble members ![]() $1 \rightarrow 5000$ and
$1 \rightarrow 5000$ and ![]() $5001 \rightarrow 10\,000$, and dividing by the
$5001 \rightarrow 10\,000$, and dividing by the ![]() $L^2$ norm of the ensemble average of all the ensemble members. We see that increasing the number of states increases the fidelity of the discrete representation and that the local diffusivity yields a relative error of approximately
$L^2$ norm of the ensemble average of all the ensemble members. We see that increasing the number of states increases the fidelity of the discrete representation and that the local diffusivity yields a relative error of approximately ![]() $50\,\%$. Furthermore, a six-state model (as given by
$50\,\%$. Furthermore, a six-state model (as given by ![]() $N=6$) captures the empirical ensemble mean within sampling error.
$N=6$) captures the empirical ensemble mean within sampling error.

Figure 6. Ensemble mean channel Error. Here we show the relative quantitative error between an ![]() $N-$state approximation to the continuous process and the local diffusivity estimate. A six-state system is within the sampling error for the chosen source term.
$N-$state approximation to the continuous process and the local diffusivity estimate. A six-state system is within the sampling error for the chosen source term.
These errors are particular to the choice of source term and the resulting ensemble mean. The advantage of using the exact closure relation for the passive tracer is its applicability independent of the choice of source term in the tracer equation; however, a local diffusivity tensor can likely be optimized to reduce the error for a fixed source term. Similarly, using an ![]() $N$-state model could have different errors depending on the choice of source term, and it is more expedient to examine convergence to the exact operator.
$N$-state model could have different errors depending on the choice of source term, and it is more expedient to examine convergence to the exact operator.
6. Conclusions
We have introduced a conditional averaging procedure for analysing tracers advected by a stochastic flow and formulated the problem of finding a turbulence closure into solving a set of partial differential equations. When the flow statistics are modelled as a continuous-time Markov process with finite state space, the resulting system becomes tractable to compute analytically. Furthermore, we show that flow statistics with infinite state space can be approximated by ones with finite state space through a systematic discretization.
The resulting dimensionality of the equations depended on the number of variables required to describe flow statistics and the dimensionality of the flow. A flow characterized by ![]() $m$ discrete states leads to a set of
$m$ discrete states leads to a set of ![]() $m$-coupled equations of the same dimensionality as the original. A flow characterized by a continuum of statistical variables can be discretized and reduced to the former. Eliminating the system's dependence on all but the ensemble mean leads to an operator characterization of the turbulence closure, allowing for an exploration of closures that do not invoke a scale separation hypothesis.
$m$-coupled equations of the same dimensionality as the original. A flow characterized by a continuum of statistical variables can be discretized and reduced to the former. Eliminating the system's dependence on all but the ensemble mean leads to an operator characterization of the turbulence closure, allowing for an exploration of closures that do not invoke a scale separation hypothesis.
We analysed three examples – an Ornstein–Uhlenbeck process advecting a tracer in one dimension, a three-state system in arbitrary dimensions and a stochastically wandering wave in a 2-D channel – and outlined a general approach to obtaining a closure based on the spectrum of the transition probability operator. In the examples, we examined the role of non-locality in determining a statistically steady turbulence closure. Under general principles, we derived that the small velocity amplitude, weak tracer diffusivity and fast transition rate limit reduce the closure to a spatially heterogeneous tensor acting on ensemble mean gradients. Furthermore, we related this tensor to the time-integrated auto-correlation of the stochastic flow field.
We have not exhausted the number of examples the formulation offers nor simplifications leading to analytically tractable results. Interesting future directions include using Markov states estimated directly from turbulence simulations, analysing scale-separated flows, generalizing the advection-diffusion equation to reaction-advection-diffusion equations, and formulating optimal mixing problems. When the number of Markov states increases, the computational burden of estimating turbulent diffusivity operators becomes demanding; thus, there is a need to develop methods that exploit the structure of the problem as much as possible.
Mathematically, there are many challenges as well. All the arguments provided here are formal calculations, and the necessity for rigorous proofs remains. For example, a direct proof of the conditional averaging procedure is necessary. Ultimately, the goal is to reduce the stochastic-advection turbulence closure problem to one that can leverage theory from partial differential equations.
Supplementary material
Supplementary material is available at https://github.com/sandreza/StatisticalNonlocality.
Acknowledgements
We want to thank the 2018 Geophysical Fluid Dynamics Program, where a significant portion of this research was undertaken. We are also indebted to T. Bischoff, S. Byrne, R. Ferrari and G. Menon for their encouragement and insightful remarks on this manuscript. We are especially indebted to the late Charlie Doering. His expert guidance directed our path towards considering discrete velocity processes, from whence the generalization in the manuscript grew. Charlie's intellectual legacy continues to inspire and drive our work. Finally, we thank the anonymous reviewers for their constructive suggestions.
Funding
Our work is supported by the generosity of Eric and Wendy Schmidt by recommendation of the Schmidt Futures program. The Geophysical Fluid Dynamics Program is supported by the National Science Foundation, United States and the Office of Naval Research, United States. Glenn Flierl is supported by NSF grant OCE-2124211.
Declaration of interests
The authors report no conflict of interest.
Appendix A. White-noise limit and the Kraichnan ensemble
Here we wish to show how the considerations taken in the main text, specifically § 4.3, relate to Kraichnan's work with white noise in time and Gaussian process in space flow fields, see Kraichnan (Reference Kraichnan1968). We will proceed in two steps. In the first step, we show how to take a ‘white-noise’ limit of an arbitrary set of flow fields ![]() $\boldsymbol {u}_n$ and generators
$\boldsymbol {u}_n$ and generators ![]() $Q$ so that the time-integrated velocity auto-correlations stay finite. This procedure has been commented on by both Kraichnan (Reference Kraichnan1968) and Falkovich et al. (Reference Falkovich, Gawȩ dzki and Vergassola2001) as a necessary step to remove the stochastic ambiguity of a delta-correlated in time flow field. In the second step, we show how to discretize a Gaussian process to a finite state space.
$Q$ so that the time-integrated velocity auto-correlations stay finite. This procedure has been commented on by both Kraichnan (Reference Kraichnan1968) and Falkovich et al. (Reference Falkovich, Gawȩ dzki and Vergassola2001) as a necessary step to remove the stochastic ambiguity of a delta-correlated in time flow field. In the second step, we show how to discretize a Gaussian process to a finite state space.
Introduce a scale parameter ![]() $\gamma$ for each velocity state and the generator
$\gamma$ for each velocity state and the generator ![]() $Q$ as
$Q$ as
The integrated velocity autocorrelation remains invariant since the characteristic velocity scales like ![]() $U = {O}(\sqrt {\gamma })$, the characteristic time scale scales like
$U = {O}(\sqrt {\gamma })$, the characteristic time scale scales like ![]() $\tau = \mathscr {O}(\gamma ^{-1})$ and thus the integrated velocity autocorrelation is
$\tau = \mathscr {O}(\gamma ^{-1})$ and thus the integrated velocity autocorrelation is ![]() $U^2 \tau = \mathscr {O}(1)$ as
$U^2 \tau = \mathscr {O}(1)$ as ![]() $\gamma \rightarrow \infty$; however, the mean free path of a particle is now
$\gamma \rightarrow \infty$; however, the mean free path of a particle is now ![]() $\ell \propto U \tau = \mathscr {O}(1 / \sqrt {\gamma })$ and goes to zero in the limit. This limit yields a delta-correlated flow field in time as
$\ell \propto U \tau = \mathscr {O}(1 / \sqrt {\gamma })$ and goes to zero in the limit. This limit yields a delta-correlated flow field in time as ![]() $\gamma \rightarrow \infty$.
$\gamma \rightarrow \infty$.
From (4.20), we have the exact relation as ![]() $\gamma \rightarrow \infty$ for
$\gamma \rightarrow \infty$ for ![]() $j \neq 1$,
$j \neq 1$,
 \begin{align} &\sum_{(i \neq 1) n} \underbrace{(\boldsymbol{w}_j \boldsymbol{\cdot} \hat{\boldsymbol{e}}_n)(\boldsymbol{\hat{e}}_n \boldsymbol{\cdot} \boldsymbol{v}_i ) \boldsymbol{\nabla} \boldsymbol{\cdot} ( \sqrt{\gamma} \boldsymbol{u}_n}_{\mathscr{O}(\sqrt{\gamma})} \varphi_i ) - \underbrace{\kappa \Delta}_{\mathscr{O}(1)} \varphi_j- \underbrace{\gamma \lambda_j}_{\mathscr{O}(\gamma)} \varphi_j\nonumber\\ &\quad ={-} \sum_n \underbrace{P_n (\boldsymbol{w}_j \boldsymbol{\cdot} \hat{\boldsymbol{e}}_n) \boldsymbol{\nabla} \boldsymbol{\cdot} ( \sqrt{\gamma} \boldsymbol{u}_n}_{\mathscr{O}(\sqrt{\gamma})} \varphi_1 ) . \end{align}
\begin{align} &\sum_{(i \neq 1) n} \underbrace{(\boldsymbol{w}_j \boldsymbol{\cdot} \hat{\boldsymbol{e}}_n)(\boldsymbol{\hat{e}}_n \boldsymbol{\cdot} \boldsymbol{v}_i ) \boldsymbol{\nabla} \boldsymbol{\cdot} ( \sqrt{\gamma} \boldsymbol{u}_n}_{\mathscr{O}(\sqrt{\gamma})} \varphi_i ) - \underbrace{\kappa \Delta}_{\mathscr{O}(1)} \varphi_j- \underbrace{\gamma \lambda_j}_{\mathscr{O}(\gamma)} \varphi_j\nonumber\\ &\quad ={-} \sum_n \underbrace{P_n (\boldsymbol{w}_j \boldsymbol{\cdot} \hat{\boldsymbol{e}}_n) \boldsymbol{\nabla} \boldsymbol{\cdot} ( \sqrt{\gamma} \boldsymbol{u}_n}_{\mathscr{O}(\sqrt{\gamma})} \varphi_1 ) . \end{align}
Since the integrated autocorrelation of velocity is independent of ![]() $\gamma$, we assume
$\gamma$, we assume ![]() $\varphi _1 = \mathscr {O}(1)$, which yields the leading order balance
$\varphi _1 = \mathscr {O}(1)$, which yields the leading order balance
 \begin{equation} \underbrace{\gamma \lambda_j}_{\mathscr{O}(\gamma)} \varphi_j \approx \sum_n \underbrace{P_n (\boldsymbol{w}_j \boldsymbol{\cdot} \hat{\boldsymbol{e}}_n) \boldsymbol{\nabla} \boldsymbol{\cdot} ( \sqrt{\gamma} \boldsymbol{u}_n \varphi_1 ) }_{\mathscr{O}(\sqrt{\gamma})}. \end{equation}
\begin{equation} \underbrace{\gamma \lambda_j}_{\mathscr{O}(\gamma)} \varphi_j \approx \sum_n \underbrace{P_n (\boldsymbol{w}_j \boldsymbol{\cdot} \hat{\boldsymbol{e}}_n) \boldsymbol{\nabla} \boldsymbol{\cdot} ( \sqrt{\gamma} \boldsymbol{u}_n \varphi_1 ) }_{\mathscr{O}(\sqrt{\gamma})}. \end{equation}
The above relation was assumed in (4.25) but is now justified as a particular asymptotic limit. Consequently, ![]() $\varphi _j = \mathscr {O}( 1 / \sqrt {\gamma } )$ as
$\varphi _j = \mathscr {O}( 1 / \sqrt {\gamma } )$ as ![]() $\gamma \rightarrow \infty$ for
$\gamma \rightarrow \infty$ for ![]() $j \neq 1$. Hence, the perturbation terms are small, consistent with the requirements of a local diffusivity estimate. We note that the assumption
$j \neq 1$. Hence, the perturbation terms are small, consistent with the requirements of a local diffusivity estimate. We note that the assumption ![]() $\varphi _1 = \mathscr {O}(1)$ is self-consistent. These calculations complete the first step.
$\varphi _1 = \mathscr {O}(1)$ is self-consistent. These calculations complete the first step.
We have seen how to rescale and take limits to get a local diffusivity estimate from an arbitrary ![]() $Q$ matrix and velocity states. The only additional ingredient to connect the present work to the Kraichnan ensemble is to observe that a Gaussian process is a structured matrix version of
$Q$ matrix and velocity states. The only additional ingredient to connect the present work to the Kraichnan ensemble is to observe that a Gaussian process is a structured matrix version of ![]() $Q$ with particular choices for the velocity states. The Karhunen–Loéve expansion implies that the Gaussian process velocity field (at a fixed time
$Q$ with particular choices for the velocity states. The Karhunen–Loéve expansion implies that the Gaussian process velocity field (at a fixed time ![]() $t$) is represented as
$t$) is represented as
 \begin{equation} \boldsymbol{u}_{\boldsymbol{\omega}}(\boldsymbol{x}, t) = \sum_{n=1}^\infty A_{\omega_n}(t) \boldsymbol{\varPhi}_n(\boldsymbol{x}), \end{equation}
\begin{equation} \boldsymbol{u}_{\boldsymbol{\omega}}(\boldsymbol{x}, t) = \sum_{n=1}^\infty A_{\omega_n}(t) \boldsymbol{\varPhi}_n(\boldsymbol{x}), \end{equation}
where each ![]() $A_{\omega _n}(t)$ is, for example, an independent Ornstein–Uhlenbeck process (although any process with a Gaussian stationary distribution will suffice) with integrated autocorrelation one and
$A_{\omega _n}(t)$ is, for example, an independent Ornstein–Uhlenbeck process (although any process with a Gaussian stationary distribution will suffice) with integrated autocorrelation one and ![]() $\boldsymbol {\varPhi }_n(\boldsymbol {x})$ are eigenvectors of the covariance tensor associated with the Gaussian process. They satisfy the relation
$\boldsymbol {\varPhi }_n(\boldsymbol {x})$ are eigenvectors of the covariance tensor associated with the Gaussian process. They satisfy the relation
where ![]() $\varLambda _n$ are the eigenvalues of the covariance tensor.
$\varLambda _n$ are the eigenvalues of the covariance tensor.
We now show how to express the above infinite-dimensional state space as a limit of the finite-dimensional ones. Represent each amplitude ![]() $A_{\omega _n}$ as an
$A_{\omega _n}$ as an ![]() $N$-state model with transition matrix
$N$-state model with transition matrix ![]() $\tilde {\mathcal {Q}}$ (as was done for the Ornstein–Uhlenbeck process) and observe that each one is independent. The
$\tilde {\mathcal {Q}}$ (as was done for the Ornstein–Uhlenbeck process) and observe that each one is independent. The ![]() $Q$ matrix becomes a Kronecker sum of infinitely many copies of the same
$Q$ matrix becomes a Kronecker sum of infinitely many copies of the same ![]() $\tilde {Q}$. In practice, this infinite Kronecker sum is truncated to a finite number, let us say the first
$\tilde {Q}$. In practice, this infinite Kronecker sum is truncated to a finite number, let us say the first ![]() $M$ of them as ordered by the eigenvalues
$M$ of them as ordered by the eigenvalues ![]() $\varLambda _n$ of the covariance tensor. The resulting discrete states are then given by the product of
$\varLambda _n$ of the covariance tensor. The resulting discrete states are then given by the product of ![]() $N$ possible modal amplitudes for a fixed basis function
$N$ possible modal amplitudes for a fixed basis function ![]() $\boldsymbol {\varPhi }$ with
$\boldsymbol {\varPhi }$ with ![]() $M$ total number of independent modes, hence, an
$M$ total number of independent modes, hence, an ![]() $N^M$ finite dimensional space. More concretely, if we discretize with three modal amplitudes and each modal amplitude with a two-state system, then each amplitude is either
$N^M$ finite dimensional space. More concretely, if we discretize with three modal amplitudes and each modal amplitude with a two-state system, then each amplitude is either ![]() $+1$ or
$+1$ or ![]() $-1$, leading to a total possible
$-1$, leading to a total possible ![]() $2^3 = 8$ pairings, e.g.
$2^3 = 8$ pairings, e.g.
and the Kronecker sum matrix
 \begin{gather}Q = \tilde{Q} \oplus \tilde{Q} \oplus \tilde{Q} = \frac{1}{2} \begin{bmatrix} -3 & 1 & 1 & 0 & 1 & 0 & 0 & 0 \\ 1 & -3 & 0 & 1 & 0 & 1 & 0 & 0 \\ 1 & 0 & -3 & 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 1 & -3 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & -3 & 1 & 1 & 0 \\ 0 & 1 & 0 & 0 & 1 & -3 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 & -3 & 1 \\ 0 & 0 & 0 & 1 & 0 & 1 & 1 & -3 \end{bmatrix}, \end{gather}
\begin{gather}Q = \tilde{Q} \oplus \tilde{Q} \oplus \tilde{Q} = \frac{1}{2} \begin{bmatrix} -3 & 1 & 1 & 0 & 1 & 0 & 0 & 0 \\ 1 & -3 & 0 & 1 & 0 & 1 & 0 & 0 \\ 1 & 0 & -3 & 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 1 & -3 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & -3 & 1 & 1 & 0 \\ 0 & 1 & 0 & 0 & 1 & -3 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 & -3 & 1 \\ 0 & 0 & 0 & 1 & 0 & 1 & 1 & -3 \end{bmatrix}, \end{gather}where each transition corresponds to a single sign flip of the Gaussian process basis functions that constitute the velocity states.
Given that our analysis was performed for an arbitrary-sized ![]() $Q$ matrix, we use finite truncations and then take limits afterward. Note the order of the limits taken: first, truncate to a finite state space, next, take the white noise limit, then lastly, take the limit to the infinite state space. Those limits, taken in that order, yield the same model as that of Kraichnan (Reference Kraichnan1968).
$Q$ matrix, we use finite truncations and then take limits afterward. Note the order of the limits taken: first, truncate to a finite state space, next, take the white noise limit, then lastly, take the limit to the infinite state space. Those limits, taken in that order, yield the same model as that of Kraichnan (Reference Kraichnan1968).
Appendix B. An alternative formal derivation
We wish to show that one can work directly with the continuous formulation of the advection-diffusion equations for the derivation of the conditional mean equations. Although we consider a finite (but arbitrarily large) number of Markov states here, considering a continuum follows mutatis mutandi. In § 2, we wrote down the master equation for the discretized stochastic system as
 \begin{equation} \partial_t \rho_m = \sum_{i} \frac{\partial}{\partial \theta^i} \left[ \left( \sum_{jkc} A_{ijk}^c u^{k,c}_m \theta^j - \sum_j D_{ij} \theta^j - s^i \right ) \rho_m \right] + \sum_n \mathcal{Q}_{mn} \rho_n . \end{equation}
\begin{equation} \partial_t \rho_m = \sum_{i} \frac{\partial}{\partial \theta^i} \left[ \left( \sum_{jkc} A_{ijk}^c u^{k,c}_m \theta^j - \sum_j D_{ij} \theta^j - s^i \right ) \rho_m \right] + \sum_n \mathcal{Q}_{mn} \rho_n . \end{equation}
We introduce the (spatial) volume element ![]() $\Delta \boldsymbol {x}_i$ to rewrite (B1) in the evocative manner,
$\Delta \boldsymbol {x}_i$ to rewrite (B1) in the evocative manner,
 \begin{equation} \partial_t \rho_m = \sum_{i} \Delta \boldsymbol{x}_i \frac{1}{\Delta \boldsymbol{x}_i} \frac{\partial}{\partial \theta^i} \left[ \left( \sum_{jkc} A_{ijk}^c u^{k,c}_m \theta^j - \sum_j D_{ij} \theta^j - s^i \right ) \rho_m \right] + \sum_n \mathcal{Q}_{mn} \rho_n . \end{equation}
\begin{equation} \partial_t \rho_m = \sum_{i} \Delta \boldsymbol{x}_i \frac{1}{\Delta \boldsymbol{x}_i} \frac{\partial}{\partial \theta^i} \left[ \left( \sum_{jkc} A_{ijk}^c u^{k,c}_m \theta^j - \sum_j D_{ij} \theta^j - s^i \right ) \rho_m \right] + \sum_n \mathcal{Q}_{mn} \rho_n . \end{equation}We now take limits
to get the functional evolution equation for the probability density,
where ![]() $\boldsymbol {x}$ is a continuous index. The notation here is similar to that of Zinn-Justin (Reference Zinn-Justin2021, § 35). As before, we can derive the conditionally averaged equations directly from the above. To do so, we make the additional correspondence
$\boldsymbol {x}$ is a continuous index. The notation here is similar to that of Zinn-Justin (Reference Zinn-Justin2021, § 35). As before, we can derive the conditionally averaged equations directly from the above. To do so, we make the additional correspondence
We now define the same quantities as before, but using the field integral
The discrete indices ![]() $i,j,k$ in the equations from § 2 are replaced by continuous labels
$i,j,k$ in the equations from § 2 are replaced by continuous labels ![]() $\boldsymbol {x}$ and
$\boldsymbol {x}$ and ![]() $\boldsymbol {y}$. We only use a few formal properties of the field integral, with direct correspondence to
$\boldsymbol {y}$. We only use a few formal properties of the field integral, with direct correspondence to ![]() $n$-dimensional integrals. We use linearity, i.e. for two mappings with compatible ranges
$n$-dimensional integrals. We use linearity, i.e. for two mappings with compatible ranges ![]() $\mathcal {F}[\theta ]$ and
$\mathcal {F}[\theta ]$ and ![]() $\mathcal {H}[\theta ]$,
$\mathcal {H}[\theta ]$,
We use the analogue to the divergence theorem,
 \begin{align} \int \mathcal{D}[\theta] \int \,{\rm d} \boldsymbol{x} \frac{\delta}{\delta \theta (\boldsymbol{x} )} \left( \left[ \boldsymbol{u}_m \boldsymbol{\cdot} \boldsymbol{\nabla} \theta - \kappa \Delta \theta - s \right] \rho_m \right) &= 0\\ &\Leftrightarrow\nonumber\end{align}
\begin{align} \int \mathcal{D}[\theta] \int \,{\rm d} \boldsymbol{x} \frac{\delta}{\delta \theta (\boldsymbol{x} )} \left( \left[ \boldsymbol{u}_m \boldsymbol{\cdot} \boldsymbol{\nabla} \theta - \kappa \Delta \theta - s \right] \rho_m \right) &= 0\\ &\Leftrightarrow\nonumber\end{align}
since the integral of a divergence should be zero if the probabilities vanish at infinity (i.e. that our tracer cannot have infinite values at a given point in space). We also make use of the integration by parts, i.e. for some functionals ![]() $\mathcal {F}$ and
$\mathcal {F}$ and ![]() $\mathcal {H}$,
$\mathcal {H}$,
 \begin{align} \int \mathcal{D}[\theta] \mathcal{H} \int \,{\rm d} \boldsymbol{x} \frac{\delta}{\delta \theta (\boldsymbol{x} )} \mathcal{F} &={-} \int \mathcal{D}[\theta] \int \,{\rm d} \boldsymbol{x} \frac{\delta \mathcal{H} }{\delta \theta (\boldsymbol{x} )} \mathcal{F}\\ &\Leftrightarrow\nonumber \end{align}
\begin{align} \int \mathcal{D}[\theta] \mathcal{H} \int \,{\rm d} \boldsymbol{x} \frac{\delta}{\delta \theta (\boldsymbol{x} )} \mathcal{F} &={-} \int \mathcal{D}[\theta] \int \,{\rm d} \boldsymbol{x} \frac{\delta \mathcal{H} }{\delta \theta (\boldsymbol{x} )} \mathcal{F}\\ &\Leftrightarrow\nonumber \end{align}And finally, we also interchange sums and integrals,
 \begin{align} \int \mathcal{D}[\theta ] (\Delta \theta) \rho_m &= \Delta \int \mathcal{D}[\theta] \theta \rho_m = \Delta \varTheta_m\\ &\Leftrightarrow\nonumber \end{align}
\begin{align} \int \mathcal{D}[\theta ] (\Delta \theta) \rho_m &= \Delta \int \mathcal{D}[\theta] \theta \rho_m = \Delta \varTheta_m\\ &\Leftrightarrow\nonumber \end{align} \begin{align} \int \,{\rm d} \boldsymbol{\theta} \left( \sum_j D_{\ell j} \theta^j \rho_m \right) &= \sum_j D_{\ell j} \int \,{\rm d} \boldsymbol{\theta} \theta^j \rho_m = \sum_j D_{\ell j} \varTheta^j_m . \end{align}
\begin{align} \int \,{\rm d} \boldsymbol{\theta} \left( \sum_j D_{\ell j} \theta^j \rho_m \right) &= \sum_j D_{\ell j} \int \,{\rm d} \boldsymbol{\theta} \theta^j \rho_m = \sum_j D_{\ell j} \varTheta^j_m . \end{align}
We proceed similarly for the ![]() $\boldsymbol {u}_m \boldsymbol {\cdot } \boldsymbol {\nabla }$ term. We also use properties of the variational derivative, such as,
$\boldsymbol {u}_m \boldsymbol {\cdot } \boldsymbol {\nabla }$ term. We also use properties of the variational derivative, such as,
Taken together, one can directly obtain (2.13) and (2.14) by first integrating (B6) with respect to ![]() $\mathcal {D}[\theta ]$ to get
$\mathcal {D}[\theta ]$ to get
and multiplying (B6) by ![]() $\theta (\,\boldsymbol {y})$ and then integrating with respect to
$\theta (\,\boldsymbol {y})$ and then integrating with respect to ![]() $\mathcal {D}[\theta ]$ to get
$\mathcal {D}[\theta ]$ to get
In the above expression, removing explicit dependence of the position variable yields
Our reason for mentioning the above methodology is that it allows for expedited computations. There is no need to explicitly discretize, perform usual ![]() $n$-dimensional integral manipulations and then take limits afterward. For example, computing the conditional two-moment equations defined by the variable
$n$-dimensional integral manipulations and then take limits afterward. For example, computing the conditional two-moment equations defined by the variable
is obtained by multiplying (B6) by ![]() $\theta (\,\boldsymbol {y})$ and
$\theta (\,\boldsymbol {y})$ and ![]() $\theta (\boldsymbol {z})$, and integrating with respect to
$\theta (\boldsymbol {z})$, and integrating with respect to ![]() $\mathcal {D}[\theta ]$,
$\mathcal {D}[\theta ]$,
 $$\begin{gather} \partial_t C_m + \boldsymbol{\nabla}_{\boldsymbol{y}} \boldsymbol{\cdot} \left( \boldsymbol{u}_m (\,\boldsymbol{y}) C_m - \kappa \boldsymbol{\nabla}_{\boldsymbol{y}} C_m \right) + \boldsymbol{\nabla}_{\boldsymbol{z}} \boldsymbol{\cdot} \left( \boldsymbol{u}_m(\boldsymbol{z}) C_m - \kappa \boldsymbol{\nabla}_{\boldsymbol{z}} C_m \right)\nonumber\\ = s(\boldsymbol{z}) \varTheta_m(\,\boldsymbol{y}) + s(\,\boldsymbol{y}) \varTheta_m(\boldsymbol{z}) + \sum_{n}\mathcal{Q}_{mn} C_n . \end{gather}$$
$$\begin{gather} \partial_t C_m + \boldsymbol{\nabla}_{\boldsymbol{y}} \boldsymbol{\cdot} \left( \boldsymbol{u}_m (\,\boldsymbol{y}) C_m - \kappa \boldsymbol{\nabla}_{\boldsymbol{y}} C_m \right) + \boldsymbol{\nabla}_{\boldsymbol{z}} \boldsymbol{\cdot} \left( \boldsymbol{u}_m(\boldsymbol{z}) C_m - \kappa \boldsymbol{\nabla}_{\boldsymbol{z}} C_m \right)\nonumber\\ = s(\boldsymbol{z}) \varTheta_m(\,\boldsymbol{y}) + s(\,\boldsymbol{y}) \varTheta_m(\boldsymbol{z}) + \sum_{n}\mathcal{Q}_{mn} C_n . \end{gather}$$In particular, we note the source term on the right-hand side and the appearance of the first conditional moment. In the derivation, we used the product rule
If the advection-diffusion equation is ![]() $m$-dimensional and we have
$m$-dimensional and we have ![]() $N$ Markov states, the above equation is made up of
$N$ Markov states, the above equation is made up of ![]() $N$ coupled
$N$ coupled ![]() $2m$ dimensional partial differential equations. Indeed the equation for the
$2m$ dimensional partial differential equations. Indeed the equation for the ![]() $M$th moment is made up of
$M$th moment is made up of ![]() $N$ coupled
$N$ coupled ![]() $M \times m$ dimensional partial differential equations.
$M \times m$ dimensional partial differential equations.
Appendix C. A heuristic overview of the master equation and discretizations
In this section, we provide an argument for the form of the master equation in the main text, (2.18) in § 2. Our starting point is § C.1, where we use the Liouville equation for two continuous variables. We then apply the finite volume method to the Fokker–Planck equation of an Ornstein–Uhlenbeck process to derive the transition matrices used in the two-state and three-state systems in § 3. We conclude with a formal argument for the use of discrete Markov states as an approximation to the compressible Euler equations in § C.4.
C.1. Two-variable system
Suppose that we have two variables ![]() $x, y \in \mathbb {R}$ governed by the equations
$x, y \in \mathbb {R}$ governed by the equations
where ![]() $\xi$ is white noise. In this context, we think of
$\xi$ is white noise. In this context, we think of ![]() $x$ as being our flow field
$x$ as being our flow field ![]() $\boldsymbol {u}$ and
$\boldsymbol {u}$ and ![]() $y$ as the tracer
$y$ as the tracer ![]() $\theta$. The master equation implied by the dynamics is
$\theta$. The master equation implied by the dynamics is
We now discretize the equation with respect to the ![]() $x-$variable by partitioning space into non-overlapping cells, characterized by domains
$x-$variable by partitioning space into non-overlapping cells, characterized by domains ![]() $\varOmega _m$. First, we start with the Fokker–Planck equation for
$\varOmega _m$. First, we start with the Fokker–Planck equation for ![]() $x$, which is independent of the
$x$, which is independent of the ![]() $y-$variable,
$y-$variable,
Observe the relation ![]() $\int \rho (x,y,t) \,{{\rm d} y} = P(x,t)$. Define our coarse grained variable
$\int \rho (x,y,t) \,{{\rm d} y} = P(x,t)$. Define our coarse grained variable ![]() $\mathcal {P}_m$ as
$\mathcal {P}_m$ as
which is a probability. Thus, the discretization of (C4) becomes
 \begin{align} \partial_t \int_{\varOmega_m} P \,{{\rm d} x} &={-} \int_{\varOmega_m} \partial_x \left(f(x) P - \sigma^2 \partial_x P \right) \,{{\rm d} x}\\ &\approx\nonumber \end{align}
\begin{align} \partial_t \int_{\varOmega_m} P \,{{\rm d} x} &={-} \int_{\varOmega_m} \partial_x \left(f(x) P - \sigma^2 \partial_x P \right) \,{{\rm d} x}\\ &\approx\nonumber \end{align}
for a generator ![]() $\mathcal {Q}$ which we derive in (C.2) with respect to a chosen numerical flux. Heuristically, going from (C6) to (C7) is accomplished by observing that
$\mathcal {Q}$ which we derive in (C.2) with respect to a chosen numerical flux. Heuristically, going from (C6) to (C7) is accomplished by observing that ![]() $\mathcal {P}_m$ is a probability and the operator
$\mathcal {P}_m$ is a probability and the operator ![]() $\mathcal {L} \equiv \partial _x (f(x) \bullet - \sigma ^2 \partial _x \bullet )$ is linear; thus, upon discretization, the operator is represented a matrix acting on the chosen coarse grained variables
$\mathcal {L} \equiv \partial _x (f(x) \bullet - \sigma ^2 \partial _x \bullet )$ is linear; thus, upon discretization, the operator is represented a matrix acting on the chosen coarse grained variables ![]() $\mathcal {P}_n$. (It is, of course, possible to approximate using a nonlinear operator, but for simplicity, we only consider the linear case.) The property
$\mathcal {P}_n$. (It is, of course, possible to approximate using a nonlinear operator, but for simplicity, we only consider the linear case.) The property ![]() $\sum _m \mathcal {Q}_{mn} = \boldsymbol {0}$ is the discrete conservation of probability.
$\sum _m \mathcal {Q}_{mn} = \boldsymbol {0}$ is the discrete conservation of probability.
Going back to (C3), defining
introducing ![]() $x_m \in \varOmega _m$, and performing the same discretization for the joint Markov system yields
$x_m \in \varOmega _m$, and performing the same discretization for the joint Markov system yields
where we used the approximation
The ![]() $x_m$ are the Markov states and the
$x_m$ are the Markov states and the ![]() $\mathcal {Q}_{mn}$ serves as the specification for transitioning between different states. We also observe that one can simply start with the discrete states for
$\mathcal {Q}_{mn}$ serves as the specification for transitioning between different states. We also observe that one can simply start with the discrete states for ![]() $x$ and continuous variables for
$x$ and continuous variables for ![]() $y$ to directly obtain (C9), as was done in the main text.
$y$ to directly obtain (C9), as was done in the main text.
In what follows, we give a concrete example of deriving a generator ![]() $\mathcal {Q}$ from a finite-volume discretization of an Ornstein–Uhlenbeck (OU) process. We explicitly mention the kind of discretization that we use since retaining mimetic properties of the generator
$\mathcal {Q}$ from a finite-volume discretization of an Ornstein–Uhlenbeck (OU) process. We explicitly mention the kind of discretization that we use since retaining mimetic properties of the generator ![]() $\mathcal {Q}$ is not guaranteed with other discretizations. Furthermore, using a finite volume discretization allows for the resulting discretization to be interpreted as a continuous-time Markov process with a finite state space.
$\mathcal {Q}$ is not guaranteed with other discretizations. Furthermore, using a finite volume discretization allows for the resulting discretization to be interpreted as a continuous-time Markov process with a finite state space.
C.2. Example discretization
Consider an Ornstein–Uhlenbeck process and the resulting Fokker–Planck equation,
We discretize the above equation with ![]() $N+1$ cells, where
$N+1$ cells, where ![]() $N = 1$ and
$N = 1$ and ![]() $N = 2$ correspond to the two- and three-state systems, respectively. Using a finite volume discretization, we take our cells to be
$N = 2$ correspond to the two- and three-state systems, respectively. Using a finite volume discretization, we take our cells to be
for ![]() $m = 0, 1,\ldots, N$. Our choice implies that cell centres (the discrete Markov states) are
$m = 0, 1,\ldots, N$. Our choice implies that cell centres (the discrete Markov states) are
for ![]() $m = 0 ,\ldots, N$, and cell faces are
$m = 0 ,\ldots, N$, and cell faces are
for ![]() $m = 0,\ldots, N+1$. We define
$m = 0,\ldots, N+1$. We define
Upon integrating with respect to the control volume, we obtain
The numerical flux is chosen as follows:
where we use the convention ![]() $\mathcal {P}_{-1} = \mathcal {P}_{N+1} = 0$ so that boundaries, corresponding to indices
$\mathcal {P}_{-1} = \mathcal {P}_{N+1} = 0$ so that boundaries, corresponding to indices ![]() $m=0$ and
$m=0$ and ![]() $m=N+1$, imply no flux conditions. Combining the flux estimates for both cell boundaries, the evolution equation for the probabilities
$m=N+1$, imply no flux conditions. Combining the flux estimates for both cell boundaries, the evolution equation for the probabilities ![]() $\mathcal {P}_m$ becomes
$\mathcal {P}_m$ becomes
which implies the generator
Equation (C21) emphasizes the row structure of the matrix whereas (C22) emphasizes the column structure. The steady state probability distribution is the binomial distribution
(The continuous steady state distribution is a Normal distribution ![]() $\rho (x) = (2{\rm \pi} )^{-1/2} \exp ( -x^2/2 )$.) Furthermore, the eigenvectors and eigenvalues of the matrix are in correspondence with the eigenfunctions and eigenvalues of the Ornstein–Uhlenbeck process as noted by Hagan et al. (Reference Hagan, Doering and Levermore1989). In particular, the cell centre vector, (C26), is a left eigenvector of
$\rho (x) = (2{\rm \pi} )^{-1/2} \exp ( -x^2/2 )$.) Furthermore, the eigenvectors and eigenvalues of the matrix are in correspondence with the eigenfunctions and eigenvalues of the Ornstein–Uhlenbeck process as noted by Hagan et al. (Reference Hagan, Doering and Levermore1989). In particular, the cell centre vector, (C26), is a left eigenvector of ![]() $\mathcal {Q}_{mn}$ with eigenvalue
$\mathcal {Q}_{mn}$ with eigenvalue ![]() $\lambda = -1$. This relation is useful for calculating the auto-correlation of the Markov process since (4.35) only involves one eigenvalue. We used the generator, (C22), in the construction of the two- and three-state systems.
$\lambda = -1$. This relation is useful for calculating the auto-correlation of the Markov process since (4.35) only involves one eigenvalue. We used the generator, (C22), in the construction of the two- and three-state systems.
C.3. Example discretization 2
Consider a random walk with drift in a periodic domain and the resulting Fokker–Planck equation,
We use control volumes,
for ![]() $m = 0, 1,\ldots, N-1$. Our choice implies that cell centres are
$m = 0, 1,\ldots, N-1$. Our choice implies that cell centres are
for ![]() $m = 0 ,\ldots, N-1$, and cell faces are
$m = 0 ,\ldots, N-1$, and cell faces are
for ![]() $m = 0,\ldots, N-1$. Using a central flux for the advective term, the standard flux for the diffusive term, and accounting for periodicity yields the matrices
$m = 0,\ldots, N-1$. Using a central flux for the advective term, the standard flux for the diffusive term, and accounting for periodicity yields the matrices
for ![]() $i = 1,\ldots, N$ and zero otherwise. Here,
$i = 1,\ldots, N$ and zero otherwise. Here, ![]() $\%$ is the modulus operation and accounts for super/sub diagonals of the matrices along with periodicity.
$\%$ is the modulus operation and accounts for super/sub diagonals of the matrices along with periodicity.
The transition matrix is then
With regards to the calculations in § 5, we take our stream function states to be
for m = ![]() $0, 1,\ldots, N-1$.
$0, 1,\ldots, N-1$.
C.4. A finite volume approximation in function space
We start with the compressible Euler equations
where ![]() $\rho$ is density,
$\rho$ is density, ![]() $\rho \boldsymbol {u}$ is the momentum,
$\rho \boldsymbol {u}$ is the momentum, ![]() $\boldsymbol {u} = \rho \boldsymbol {u} / \rho$ is the velocity,
$\boldsymbol {u} = \rho \boldsymbol {u} / \rho$ is the velocity, ![]() $\rho e$ is the total energy density and
$\rho e$ is the total energy density and ![]() $p$ is a thermodynamic pressure. (For example, one could use the pressure for an ideal gas
$p$ is a thermodynamic pressure. (For example, one could use the pressure for an ideal gas ![]() $p = (\gamma - 1) (\rho e - \rho |\boldsymbol {u}|^2 /2)$ with
$p = (\gamma - 1) (\rho e - \rho |\boldsymbol {u}|^2 /2)$ with ![]() $\gamma = 7/5$.) Here, we introduce
$\gamma = 7/5$.) Here, we introduce ![]() $Z$ as a probability density in function space for the state variables
$Z$ as a probability density in function space for the state variables ![]() $S \equiv (\rho, \rho \boldsymbol {u} , \rho e)$. In the notation of Appendix B, the evolution equation for the statistics
$S \equiv (\rho, \rho \boldsymbol {u} , \rho e)$. In the notation of Appendix B, the evolution equation for the statistics ![]() $Z$ are
$Z$ are
 \begin{align} \partial_t Z &= \int
\,{\rm d}\boldsymbol{x} \left[ \frac{\delta}{\delta
\rho}\left( \boldsymbol{\nabla} \boldsymbol{\cdot}
\left[\rho \boldsymbol{u} \right] Z \right) +
\frac{\delta}{\delta \rho \boldsymbol{u} }\left(
\boldsymbol{\nabla} \boldsymbol{\cdot} \left[ \rho
\boldsymbol{u} \otimes \boldsymbol{u} \right] Z +
\boldsymbol{\nabla} p Z \right)\right.\nonumber\\ &\left.\quad+\, \frac{\delta}{ \delta
\rho e} \left( \boldsymbol{\nabla} \boldsymbol{\cdot}
\left( \boldsymbol{u} \left[ \rho e + p \right] \right) Z
\right) \right] ,
\end{align}
\begin{align} \partial_t Z &= \int
\,{\rm d}\boldsymbol{x} \left[ \frac{\delta}{\delta
\rho}\left( \boldsymbol{\nabla} \boldsymbol{\cdot}
\left[\rho \boldsymbol{u} \right] Z \right) +
\frac{\delta}{\delta \rho \boldsymbol{u} }\left(
\boldsymbol{\nabla} \boldsymbol{\cdot} \left[ \rho
\boldsymbol{u} \otimes \boldsymbol{u} \right] Z +
\boldsymbol{\nabla} p Z \right)\right.\nonumber\\ &\left.\quad+\, \frac{\delta}{ \delta
\rho e} \left( \boldsymbol{\nabla} \boldsymbol{\cdot}
\left( \boldsymbol{u} \left[ \rho e + p \right] \right) Z
\right) \right] ,
\end{align}
where we have suppressed the index ![]() $\boldsymbol {x}$ in the variational derivatives.
$\boldsymbol {x}$ in the variational derivatives.
Now consider a partition in function space into domains ![]() $\varOmega _m$ and let
$\varOmega _m$ and let ![]() $S_m$ denote a value of a state within the set
$S_m$ denote a value of a state within the set ![]() $S_m$. In this case, we define the probability as
$S_m$. In this case, we define the probability as
In analogy with the calculations in § C.2, integrating (C35) with respect to a control volume ![]() $\varOmega _m$ would result in an approximation of the form
$\varOmega _m$ would result in an approximation of the form
for some generator ![]() $\mathcal {Q}_{mn}$. The entries of the generator are functionals of the states
$\mathcal {Q}_{mn}$. The entries of the generator are functionals of the states ![]() $S_m \in \varOmega _m$. Performing the necessary integrals and re-expressing it in this finite form is done indirectly through data-driven methods with time series as in Klus, Koltai & Schütte (Reference Klus, Koltai and Schütte2016), Fernex, Noack & Semaan (Reference Fernex, Noack and Semaan2021) or Maity, Koltai & Schumacher (Reference Maity, Koltai and Schumacher2022).
$S_m \in \varOmega _m$. Performing the necessary integrals and re-expressing it in this finite form is done indirectly through data-driven methods with time series as in Klus, Koltai & Schütte (Reference Klus, Koltai and Schütte2016), Fernex, Noack & Semaan (Reference Fernex, Noack and Semaan2021) or Maity, Koltai & Schumacher (Reference Maity, Koltai and Schumacher2022).
The difficulty of performing a discretization from first principles comes from choosing the subsets of function space to partition and carrying out the integrals in function space. Periodic orbits and fixed points of a flow serve as a natural skeleton for function space, but are typically burdensome to compute. We offer no solution, but hope that in the future, such direct calculations are rendered tractable. In the meanwhile, indirect data-driven methods are the most promising avenue for the calculation of the generator ![]() $\mathcal {Q}$.
$\mathcal {Q}$.