Article contents
Small perturbation evolution in compressible Poiseuille flow: pressure–velocity interactions and obliqueness effects
Published online by Cambridge University Press: 03 February 2017
Abstract
Small perturbation evolution in compressible Poiseuille flow is contrasted against the incompressible case using direct simulations and non-modal linear analysis. The onset of compressibility effects leads to a profound change in the behaviour of pressure and its interaction with the velocity field. Linear analysis shows that the most significant compressibility outcome is the harmonic coupling between pressure and wall-normal velocity perturbations. Oscillations in normal perturbations can lead to periods of negative production causing suppression of perturbation growth. The extent of the influence of compressibility can be characterized in terms of an effective gradient Mach number (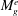 $M_{g}^{e}$). Analysis shows that
$M_{g}^{e}$). Analysis shows that 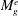 $M_{g}^{e}$ diminishes as the angle of the perturbation increases with respect to the shear plane. Direct numerical simulations show that streamwise perturbations, which would lead to Tollmien–Schlichting instability in the incompressible case, are completely suppressed in the compressible case and experience the highest
$M_{g}^{e}$ diminishes as the angle of the perturbation increases with respect to the shear plane. Direct numerical simulations show that streamwise perturbations, which would lead to Tollmien–Schlichting instability in the incompressible case, are completely suppressed in the compressible case and experience the highest 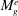 $M_{g}^{e}$. At the other extreme, computations reveal that spanwise perturbations, which experience negligible
$M_{g}^{e}$. At the other extreme, computations reveal that spanwise perturbations, which experience negligible 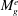 $M_{g}^{e}$, are entirely unaltered from the incompressible case. Perturbation behaviour at intermediate obliqueness angles is established. Moreover, the underlying pressure–velocity interactions are explicated.
$M_{g}^{e}$, are entirely unaltered from the incompressible case. Perturbation behaviour at intermediate obliqueness angles is established. Moreover, the underlying pressure–velocity interactions are explicated.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 12
- Cited by



