Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-19T11:41:47.372Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular behaviour of a rarefied gas on a planar boundary

Published online by Cambridge University Press:  01 February 2013

Shigeru Takata  and
Hitoshi Funagane
Shigeru Takata*
Affiliation:
Department of Mechanical Engineering and Science, Graduate School of Engineering, Kyoto University, Kyoto 606-8501, Japan Advanced Research Institute of Fluid Science and Engineering, Graduate School of Engineering, Kyoto University, Kyoto 606-8501, Japan
Hitoshi Funagane
Affiliation:
Department of Mechanical Engineering and Science, Graduate School of Engineering, Kyoto University, Kyoto 606-8501, Japan
*
†Email address for correspondence: takata.shigeru.4a@kyoto-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

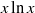Singular behaviour of a rarefied gas on a planar boundary is clarified on the basis of the Boltzmann equation. The thermal transpiration between two parallel plates is taken as a specific example. First, the flow velocity is shown to behave like $x\ln x$ in the vicinity of the boundary, where $x$ is a distance from the boundary. This implies a logarithmic divergence of the flow velocity gradient as 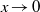$x\rightarrow 0$. Then, such a spatial singularity is shown to induce a similar singularity of the velocity distribution function (VDF) with respect to 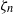${\zeta }_{n} $ on the boundary, where 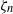${\zeta }_{n} $ is a normal component of the molecular velocity to the boundary. Moreover, the spatial singularity is shown to be quantitatively related to the discontinuity of the VDF on the boundary at 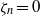${\zeta }_{n} = 0$. These macroscopic and microscopic singularities should be observed generally in a rarefied gas on a planar boundary.

JFM classification

Rarefied Gas Flow: Kinetic theory Micro-/Nano-fluid dynamics: Non-continuum effects Rarefied Gas Flow: Rarefied Gas Flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 717 , 25 February 2013 , pp. 30 - 47
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bhatnagar, P. L., Gross, E. P. & Krook, M. 1954 A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94, 511–525.Google Scholar
Bird, G. A. 1994 Molecular Gas Dynamics and the Direct Simulation of Gas Flows. Oxford.Google Scholar
Chen, C.-C., Chen, I.-K., Liu, T.-P. & Sone, Y. 2007 Thermal transpiration for the linearized Boltzmann equation. Commun. Pure Appl. Math. 60, 0147–0163.Google Scholar
Chen, I.-K., Liu, T.-P. & Takata, S. 2010 Boundary singularity for thermal transpiration problem of the linearized Boltzmann equation. Preprint, Institute of Mathematics, Academia Sinica (submitted to Arch. Rat. Mech. Anal.).Google Scholar
Holway, L. H. Jr 1963 Approximation procedures for kinetic theory. PhD thesis, Harvard University.Google Scholar
Holway, L. H. Jr 1966 New statistical models for kinetic theory: methods of construction. Phys. Fluids 9, 1658–1673.Google Scholar
Kennard, E. H. 1938 Kinetic Theory of Gases. McGraw-Hill.Google Scholar
Kosuge, S., Sato, K., Takata, S. & Aoki, K. 2005 Flows of a binary mixture of rarefied gases between two parallel plates. In Rarefied Gas Dynamics (ed. Capitelli, M.), pp. 150–155. American Institute of Physics.Google Scholar
Lilley, C. R. & Sader, J. E. 2007 Velocity gradient singularity and structure of the velocity profile in the Knudsen layer according to the Boltzmann equation. Phys. Rev. E 76, 026315.CrossRefGoogle Scholar
Lilley, C. R. & Sader, J. E. 2008 Velocity profile in the Knudsen layer according to the Boltzmann equation. Proc. R. Soc. A 464, 2015–2035.Google Scholar
Loyalka, S. K. 1971 Kinetic theory of thermal transpiration and mechanocaloric effect. I. J. Chem. Phys. 55, 4497–4503.Google Scholar
Maxwell, J. C. 1879 On stresses in rarefied gases arising from inequalities of temperature. Phil. Trans. R. Soc. 170, 231–256.Google Scholar
Niimi, H. 1971 Thermal creep flow of rarefied gas between two parallel plates. J. Phys. Soc. Jpn 30, 572–574.CrossRefGoogle Scholar
Ohwada, T., Sone, Y. & Aoki, K. 1989 Numerical analysis of the Poiseuille and thermal transpiration flows between two parallel plates on the basis of the Boltzmann equation for hard-sphere molecules. Phys. Fluids A 1, 2042–2049.Google Scholar
Sone, Y. 1964 Kinetic theory analysis of linearized Rayleigh problem. J. Phys. Soc. Jpn 19, 1463–1473.Google Scholar
Sone, Y. 1965 Effect of sudden change of wall temperature in a rarefied gas. J. Phys. Soc. Jpn 20, 222–229.Google Scholar
Sone, Y. 1966 Thermal creep in rarefied gas. J. Phys. Soc. Jpn 21, 1836–1837.Google Scholar
Sone, Y. 2007 Molecular Gas Dynamics. Birkhäuser.CrossRefGoogle Scholar
Sone, Y. & Aoki, K. 1977 Slightly rarefied gas flow over a specularly reflecting body. Phys. Fluids 20, 571–576.Google Scholar
Sone, Y. & Onishi, Y. 1978 Kinetic theory of evaporation and condensation – Hydrodynamic equation and slip boundary condition. J. Phys. Soc. Jpn 44, 1981–1994.Google Scholar
Takata, S. & Funagane, H. 2011 Poiseuille and thermal transpiration flows of a highly rarefied gas: over-concentration in the velocity distribution function. J. Fluid Mech. 669, 242–259.Google Scholar
Welander, P. 1954 On the temperature jump in a rarefied gas. Ark. Fys. 7, 507–553.Google Scholar
Williams, M. M. R. 1971 Boundary-value problems in the kinetic theory of gases. Part 2. Thermal creep. J. Fluid Mech. 45, 759–768.Google Scholar