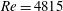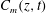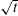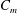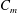1. Introduction
Shear-flow dispersion (Taylor Reference Taylor1953, Reference Taylor1954b ; Aris Reference Aris1956) is one of the primary sources of mixing in integral models for passive scalar transport and as such has wide-ranging practical applications, including contaminant transport in the atmosphere and ocean, nutrient delivery, the spread of smoke from fires and the discharge of waste effluent in streams (see, e.g. Fischer et al. Reference Fischer, List, Koh, Imberger and Brooks1979). Caused by lateral (cross-stream) gradients in a mean velocity, shear-flow dispersion was first identified by Taylor (Reference Taylor1953), who examined the transport of a solute in both laminar (Taylor Reference Taylor1953) and turbulent (Taylor Reference Taylor1954b ) pipe flow. It was demonstrated that for sufficiently large times (Taylor Reference Taylor1954a ) the effective longitudinal (streamwise) mixing is determined by a balance between longitudinal advection and radial mixing.

Figure 1. Longitudinal mixing processes in a pipe flow.
The canonical example of shear-flow dispersion is the release of a passive scalar into a bounded one-dimensional flow in a pipe or a plane channel (see figure 1). At
![]() $t=0$
, one assumes that the mean scalar concentration
$t=0$
, one assumes that the mean scalar concentration
![]() $\overline{c}$
, where the overline denotes an ensemble average, is uniformly distributed over the pipe for
$\overline{c}$
, where the overline denotes an ensemble average, is uniformly distributed over the pipe for
![]() $z\leqslant 0$
and equal to zero for
$z\leqslant 0$
and equal to zero for
![]() $z>0$
. One is typically interested in the integral concentration
$z>0$
. One is typically interested in the integral concentration
where the upper limit of integration
![]() $r_{d}$
corresponds to the radial extent of the flow. Hence, for a pipe of radius
$r_{d}$
corresponds to the radial extent of the flow. Hence, for a pipe of radius
![]() $r_{m}$
,
$r_{m}$
,
![]() $r_{d}=r_{m}$
and
$r_{d}=r_{m}$
and
![]() $C_{m}=r_{m}^{2}\langle \overline{c}\rangle$
, where
$C_{m}=r_{m}^{2}\langle \overline{c}\rangle$
, where
![]() $\langle \,\rangle$
denotes an average over the cross-section of the pipe. At
$\langle \,\rangle$
denotes an average over the cross-section of the pipe. At
![]() $t=0$
the dependence of
$t=0$
the dependence of
![]() $C_{m}$
on
$C_{m}$
on
![]() $z$
corresponds to a Heaviside step function. For time
$z$
corresponds to a Heaviside step function. For time
![]() $t>0$
the step change in
$t>0$
the step change in
![]() $C_{m}$
will become progressively smoother due to three distinct, yet closely related, physical processes.
$C_{m}$
will become progressively smoother due to three distinct, yet closely related, physical processes.
-
{D}1 The diffusive flux
 $-{\it\kappa}\partial _{z}\overline{c}$
(molecular diffusion).
$-{\it\kappa}\partial _{z}\overline{c}$
(molecular diffusion). -
{D}2 The ensemble covariance
 $\overline{wc}-\overline{w}\,\overline{c}$
(turbulent mixing).
$\overline{wc}-\overline{w}\,\overline{c}$
(turbulent mixing). -
{D}3 The spatial covariance
 $\langle \overline{w}\,\overline{c}\rangle -\langle \overline{w}\rangle \langle \overline{c}\rangle$
(shear-flow dispersion).
$\langle \overline{w}\,\overline{c}\rangle -\langle \overline{w}\rangle \langle \overline{c}\rangle$
(shear-flow dispersion).
Here
![]() $w$
is the longitudinal velocity and
$w$
is the longitudinal velocity and
![]() ${\it\kappa}$
is the molecular diffusion coefficient. Molecular diffusion is a manifestation of an averaging operation over individual particles in the fluid and is expected to play a negligible role at large scales in high-Reynolds-number flows. Turbulent mixing is a result of the chaotic motion of the flow, the covariance
${\it\kappa}$
is the molecular diffusion coefficient. Molecular diffusion is a manifestation of an averaging operation over individual particles in the fluid and is expected to play a negligible role at large scales in high-Reynolds-number flows. Turbulent mixing is a result of the chaotic motion of the flow, the covariance
![]() $\overline{wc}-\overline{w}\,\overline{c}$
corresponding to a turbulent scalar flux. Shear-flow dispersion, on the other hand, is the result of a correlation of the average velocity
$\overline{wc}-\overline{w}\,\overline{c}$
corresponding to a turbulent scalar flux. Shear-flow dispersion, on the other hand, is the result of a correlation of the average velocity
![]() $\overline{w}$
with the average concentration
$\overline{w}$
with the average concentration
![]() $\overline{c}$
over space, and enters the problem because the integral concentration
$\overline{c}$
over space, and enters the problem because the integral concentration
![]() $C_{m}$
is the primary unknown. When regions of high mean concentration coincide spatially with regions of high longitudinal mean velocity (see figure 1),
$C_{m}$
is the primary unknown. When regions of high mean concentration coincide spatially with regions of high longitudinal mean velocity (see figure 1),
![]() $\langle \overline{w}\,\overline{c}\rangle \neq \langle \overline{w}\rangle \langle \overline{c}\rangle$
, and one finds a dispersive flux. It should be noticed that the turbulent scalar flux and the dispersive flux in D2 and D3 are defined relative to the ensemble average scalar flux,
$\langle \overline{w}\,\overline{c}\rangle \neq \langle \overline{w}\rangle \langle \overline{c}\rangle$
, and one finds a dispersive flux. It should be noticed that the turbulent scalar flux and the dispersive flux in D2 and D3 are defined relative to the ensemble average scalar flux,
![]() $\overline{w}\,\overline{c}$
, and the spatially averaged flux,
$\overline{w}\,\overline{c}$
, and the spatially averaged flux,
![]() $\langle \overline{w}\rangle \langle \overline{c}\rangle$
, respectively. In many large-scale practical applications, such as open channel flow, one finds
$\langle \overline{w}\rangle \langle \overline{c}\rangle$
, respectively. In many large-scale practical applications, such as open channel flow, one finds
![]() $\text{D}3\gg \text{D}2\gg \text{D}1$
(see e.g. Elder Reference Elder1959). Moreover, Taylor (Reference Taylor1953, Reference Taylor1954b
) demonstrated that longitudinal dispersion is inversely proportional to the turbulent diffusion coefficient associated with the flow, indicating that mixing by turbulence inhibits shear-flow dispersion. Further details can be found in appendix A, in which we summarise the dispersion theory of Taylor (Reference Taylor1953) in the context of pipe flow. For a general introduction to dispersion theory the reader is referred to Chatwin & Allen (Reference Chatwin and Allen1985).
$\text{D}3\gg \text{D}2\gg \text{D}1$
(see e.g. Elder Reference Elder1959). Moreover, Taylor (Reference Taylor1953, Reference Taylor1954b
) demonstrated that longitudinal dispersion is inversely proportional to the turbulent diffusion coefficient associated with the flow, indicating that mixing by turbulence inhibits shear-flow dispersion. Further details can be found in appendix A, in which we summarise the dispersion theory of Taylor (Reference Taylor1953) in the context of pipe flow. For a general introduction to dispersion theory the reader is referred to Chatwin & Allen (Reference Chatwin and Allen1985).
Taylor’s original analysis of pipe-flow dispersion was subsequently generalised to pipes of arbitrary cross-section by Aris (Reference Aris1956), who obtained solutions for the longitudinal moments of the solute concentration and demonstrated that the longitudinal dispersion coefficient and longitudinal turbulent diffusion coefficient are additive. Gill (Reference Gill1967) later considered a general series expansion, involving higher longitudinal derivatives of the mean concentration, to determine the radial dependence of the concentration. Subsequent work has addressed the way in which the concentration profile approaches a Gaussian form (Chatwin Reference Chatwin1970), the asymptotic behaviour for small times (Chatwin Reference Chatwin1977) and the concentration at large distances from its centre of mass (Haynes & Vanneste Reference Haynes and Vanneste2014). Following the work of Brenner (Reference Brenner1980b ), a generalised Taylor dispersion theory emerged, which was not restricted to the unidirectional flows on which previous studies had focused. Generalised Taylor dispersion theory has been applied in a wide range of fields, including sedimentation (Brenner Reference Brenner1979), flows through porous media (Brenner Reference Brenner1980a ) and chemically reacting flows (Shapiro & Brenner Reference Shapiro and Brenner1986). However, in spite of the many refinements that have been made to Taylor’s theory of dispersion it has not, to the best of the authors’ knowledge, been applied explicitly in the analysis of scalar dispersion in jets. Very recently, dispersion theory was used to develop a closure for longitudinal mixing in statistically unsteady jets (Craske & van Reeuwijk Reference Craske and van Reeuwijk2015b ). There, the closure was applied to the mean kinetic energy flux and produced results that were in good agreement with direct numerical simulation. In this work we study the canonical problem of scalar dispersion in statistically steady jets and show that the dispersion theory developed in Craske & van Reeuwijk (Reference Craske and van Reeuwijk2015b ) provides an accurate representation of the dominant mixing processes.
Passive scalar transport in turbulent jets has received significant attention in the literature (e.g. Paranthoen et al.
Reference Paranthoen, Fouari, Dupont and Lecordier1988; Tong & Warhaft Reference Tong and Warhaft1995; Warhaft Reference Warhaft2000). However, the primary focus has been on steady releases; unsteady releases, for which shear-flow dispersion is expected to be significant, have received relatively little attention. An exception is the work by Landel, Caulfield & Woods (Reference Landel, Caulfield and Woods2012), who investigated unsteady scalar transport in a two-dimensional jet, created in the laboratory by confining the jet to a narrow gap between two parallel plates. They observed that the core region of the jet, which is primarily associated with longitudinal advective transport, is surrounded by eddies that are responsible for mixing. Moreover, this structure was observed to be self-similar with height, which means that when normalised by suitable length and velocity scales the behaviour of the jet is independent of its streamwise coordinate. Longitudinal mixing was attributed to the stretching of fluid that occurs between the core and the eddies. Using a mixing-length assumption, justified by the self-similarity of the flow, Landel et al. (Reference Landel, Caulfield and Woods2012) formulated an advection–diffusion equation for the transport of the integral
![]() $C_{m}(z,t)$
of a scalar given by
$C_{m}(z,t)$
of a scalar given by
Here,
![]() $z$
is the longitudinal (streamwise) coordinate,
$z$
is the longitudinal (streamwise) coordinate,
![]() $M_{m}$
is the jet momentum flux, and
$M_{m}$
is the jet momentum flux, and
![]() $K_{a}$
and
$K_{a}$
and
![]() $K_{d}$
are empirical dimensionless parameters accounting for advection and eddy diffusivity respectively.
$K_{d}$
are empirical dimensionless parameters accounting for advection and eddy diffusivity respectively.
In spite of the fact that mixing-length models can provide only a limited representation of turbulence (Pope Reference Pope2000), Landel et al. (Reference Landel, Caulfield and Woods2012) show that (1.2) provides an accurate means of predicting integral scalar concentrations in two-dimensional jets. However, it is neither clear what physical process determines the value of
![]() $K_{a}$
and
$K_{a}$
and
![]() $K_{d}$
, nor possible to state a priori which parts of the model can be applied to axisymmetric jets. Furthermore, it is unclear whether the mixing is caused by the longitudinal turbulent scalar flux or shear-flow dispersion (or both). In this work we show that for axisymmetric jets, the longitudinal turbulent scalar flux is not able to account for the observed mixing of the scalar integral, and that it is shear-flow dispersion that is the predominant cause of the mixing.
$K_{d}$
, nor possible to state a priori which parts of the model can be applied to axisymmetric jets. Furthermore, it is unclear whether the mixing is caused by the longitudinal turbulent scalar flux or shear-flow dispersion (or both). In this work we show that for axisymmetric jets, the longitudinal turbulent scalar flux is not able to account for the observed mixing of the scalar integral, and that it is shear-flow dispersion that is the predominant cause of the mixing.
The paper is structured as follows. In § 2 we define the problem, introducing the governing equations and the variables that are of primary interest. In § 3 we describe the direct numerical simulation (hereafter DNS) used to obtain the data and describe how the ensemble average was constructed. In § 4 we demonstrate that the scalar transport can be viewed as a self-similar process by analysing the propagation speed of the scalar and its longitudinal spreading rate. We explain how Taylor’s model for shear-flow dispersion in pipes (Taylor Reference Taylor1953) can be applied to jets in § 5, and compare the resulting dispersion closure with DNS observations in § 6. We apply our dispersion closure to planar jets in § 7 (additional details are provided in appendix B), which reveals that it is in one-to-one agreement with the model proposed by Landel et al. (Reference Landel, Caulfield and Woods2012). A summary of the findings and ideas for future work are provided in § 8.
2. Problem definition
A schematic for the flow considered is provided in figure 2. The turbulent jet is statistically steady, axisymmetric and produces a mean velocity field
![]() $(\overline{u},\overline{w})$
in coordinates
$(\overline{u},\overline{w})$
in coordinates
![]() $(r,z)$
, where
$(r,z)$
, where
![]() $r$
denotes the radial and
$r$
denotes the radial and
![]() $z$
the longitudinal coordinate. For
$z$
the longitudinal coordinate. For
![]() $t<0$
, the scalar concentration is equal to zero everywhere. For
$t<0$
, the scalar concentration is equal to zero everywhere. For
![]() $t\geqslant 0$
, a continuous release of scalar is activated at the inlet (hereafter referred to as the source), which produces a front that propagates and spreads as it travels along the jet. Due to the non-uniform velocity distribution, the scalar will be advected at different rates depending on its position in the jet: fluid elements in the core regions will tend to travel faster than elements in the outer region, thereby modifying the radial distribution of the scalar downstream.
$t\geqslant 0$
, a continuous release of scalar is activated at the inlet (hereafter referred to as the source), which produces a front that propagates and spreads as it travels along the jet. Due to the non-uniform velocity distribution, the scalar will be advected at different rates depending on its position in the jet: fluid elements in the core regions will tend to travel faster than elements in the outer region, thereby modifying the radial distribution of the scalar downstream.

Figure 2. Definition sketch. The grey area represents regions to which the scalar has spread at a particular time
![]() $t$
and
$t$
and
![]() $\overline{w}$
is the ensemble average longitudinal velocity.
$\overline{w}$
is the ensemble average longitudinal velocity.
The motion of the jet is governed by the incompressible Navier–Stokes equations:
where
![]() ${\it\kappa}$
is the molecular diffusion coefficient.
${\it\kappa}$
is the molecular diffusion coefficient.
In this work the velocity field is statistically stationary and, due to the fact that the mean azimuthal component of velocity is equal to zero, swirl free. It is therefore convenient to define the time and azimuthal average velocity
![]() $\overline{\boldsymbol{u}}\equiv (\overline{u}(r,z),0,\overline{w}(r,z))$
. For the scalar concentration
$\overline{\boldsymbol{u}}\equiv (\overline{u}(r,z),0,\overline{w}(r,z))$
. For the scalar concentration
![]() $c$
, which is statistically unsteady, we restrict ourselves to an ensemble and azimuthal average
$c$
, which is statistically unsteady, we restrict ourselves to an ensemble and azimuthal average
![]() $\overline{c}(r,z,t)$
.
$\overline{c}(r,z,t)$
.
The focus of the present study is on the behaviour of integrals over lateral slices of the jet. In particular, we define the volume flux
![]() $Q_{m}(z)$
and the mean momentum flux
$Q_{m}(z)$
and the mean momentum flux
![]() $M_{m}(z)$
:
$M_{m}(z)$
:
respectively, where
![]() $r_{d}$
denotes the radial extent of the jet, which will be defined precisely in § 3. In addition to the integral scalar concentration
$r_{d}$
denotes the radial extent of the jet, which will be defined precisely in § 3. In addition to the integral scalar concentration
![]() $C_{m}$
defined in (1.1), we define the integral mean scalar flux
$C_{m}$
defined in (1.1), we define the integral mean scalar flux
![]() $F_{m}$
and the integral turbulent scalar flux
$F_{m}$
and the integral turbulent scalar flux
![]() $F_{f}$
, according to
$F_{f}$
, according to
Here,
![]() $\overline{{\it\chi}}$
denotes an ensemble average and
$\overline{{\it\chi}}$
denotes an ensemble average and
![]() ${\it\chi}^{\prime }$
a fluctuation from the ensemble average such that
${\it\chi}^{\prime }$
a fluctuation from the ensemble average such that
![]() $\overline{{\it\chi}^{\prime }}=0$
. Formally, the integral quantities above are defined in the limit
$\overline{{\it\chi}^{\prime }}=0$
. Formally, the integral quantities above are defined in the limit
![]() $r_{d}\rightarrow \infty$
, but from a practical perspective it is necessary to integrate to a finite limit. This avoids complications associated with integration limits at infinity (see e.g. Kotsovinos Reference Kotsovinos1978), allowing one to focus on the fluxes in the jet, rather than the induced ambient flow. The volume flux
$r_{d}\rightarrow \infty$
, but from a practical perspective it is necessary to integrate to a finite limit. This avoids complications associated with integration limits at infinity (see e.g. Kotsovinos Reference Kotsovinos1978), allowing one to focus on the fluxes in the jet, rather than the induced ambient flow. The volume flux
![]() $Q_{m}$
and momentum flux
$Q_{m}$
and momentum flux
![]() $M_{m}$
can be used to define characteristic length and velocity scales
$M_{m}$
can be used to define characteristic length and velocity scales
![]() $r_{m}\equiv Q_{m}/M_{m}^{1/2}$
and
$r_{m}\equiv Q_{m}/M_{m}^{1/2}$
and
![]() $w_{m}\equiv M_{m}/Q_{m}$
respectively. We define a mean concentration
$w_{m}\equiv M_{m}/Q_{m}$
respectively. We define a mean concentration
![]() $c_{m}$
for the flow from the integral concentration
$c_{m}$
for the flow from the integral concentration
![]() $C_{m}$
according to
$C_{m}$
according to
![]() $c_{m}\equiv C_{m}/r_{m}^{2}$
.
$c_{m}\equiv C_{m}/r_{m}^{2}$
.
Taking a time and ensemble average of (2.1) and (2.2) for
![]() $\mathit{Re}\equiv 2M_{m}^{1/2}/{\it\nu}\gg 1$
, and integrating over lateral slices of the jet yields the integral jet equations (see e.g. Rajaratnam Reference Rajaratnam1976; Craske & van Reeuwijk Reference Craske and van Reeuwijk2015a
)
$\mathit{Re}\equiv 2M_{m}^{1/2}/{\it\nu}\gg 1$
, and integrating over lateral slices of the jet yields the integral jet equations (see e.g. Rajaratnam Reference Rajaratnam1976; Craske & van Reeuwijk Reference Craske and van Reeuwijk2015a
)
which express volume conservation and momentum conservation respectively, and
![]() ${\it\alpha}$
is the classical entrainment coefficient (see e.g. Morton, Taylor & Turner Reference Morton, Taylor and Turner1956). It is immediately apparent from (2.6a,b
) that
${\it\alpha}$
is the classical entrainment coefficient (see e.g. Morton, Taylor & Turner Reference Morton, Taylor and Turner1956). It is immediately apparent from (2.6a,b
) that
![]() $Q_{m}=2{\it\alpha}M_{m}^{1/2}(z-z_{v})$
for a conserved momentum flux
$Q_{m}=2{\it\alpha}M_{m}^{1/2}(z-z_{v})$
for a conserved momentum flux
![]() $M_{m}$
and a virtual origin
$M_{m}$
and a virtual origin
![]() $z_{v}$
, the latter corresponding to the location at which the volume flux is equal to zero.
$z_{v}$
, the latter corresponding to the location at which the volume flux is equal to zero.
When molecular transport in the longitudinal direction is neglected, the ensemble average of (2.3) can be integrated over lateral slices of the jet to give
which is an integral conservation equation for the scalar and is the principal focus of this work. In particular, our discussion of the problem will focus on the mean and turbulent dimensionless scalar flux, defined as
respectively.
3. Simulation details
We simulate an axisymmetric turbulent jet driven by an isolated source of steady momentum flux
![]() $M_{0}$
and volume flux
$M_{0}$
and volume flux
![]() $Q_{0}$
. The source is located at the centre of the base of a cuboidal domain of size
$Q_{0}$
. The source is located at the centre of the base of a cuboidal domain of size
![]() $L_{x}L_{y}L_{z}=44^{2}\times 66$
characteristic source radii,
$L_{x}L_{y}L_{z}=44^{2}\times 66$
characteristic source radii,
![]() $r_{0}$
, where
$r_{0}$
, where
![]() $r_{0}\equiv Q_{0}/M_{0}^{1/2}$
. The motion of the jet is governed by the incompressible Navier–Stokes equations (2.1) and (2.2) in a statistically steady state. To release a passive scalar into the flow at
$r_{0}\equiv Q_{0}/M_{0}^{1/2}$
. The motion of the jet is governed by the incompressible Navier–Stokes equations (2.1) and (2.2) in a statistically steady state. To release a passive scalar into the flow at
![]() $t=0$
we impose a step change in the scalar flux at the source:
$t=0$
we impose a step change in the scalar flux at the source:
where
![]() $H$
is the Heaviside step function. Equations (2.1)–(2.3) are solved numerically using
$H$
is the Heaviside step function. Equations (2.1)–(2.3) are solved numerically using
![]() $N_{x}N_{y}N_{z}=768^{2}\times 1152$
computational cells over a Cartesian grid. The code for the DNS of (2.1)–(2.3) employs a spatial discretisation of fourth-order accuracy that conserves volume, momentum and energy. Integration in time is performed using a third-order Adams–Bashforth scheme (further details can be found in Craske & van Reeuwijk Reference Craske and van Reeuwijk2015a
). On the vertical and top faces of the domain we impose open boundary conditions that allow fluid to enter and leave the domain without modifying the entrainment rate of the jet (Craske & van Reeuwijk Reference Craske and van Reeuwijk2013). The approximately circular source at the base of the domain is obstructed by two narrow orthogonal strips of width
$N_{x}N_{y}N_{z}=768^{2}\times 1152$
computational cells over a Cartesian grid. The code for the DNS of (2.1)–(2.3) employs a spatial discretisation of fourth-order accuracy that conserves volume, momentum and energy. Integration in time is performed using a third-order Adams–Bashforth scheme (further details can be found in Craske & van Reeuwijk Reference Craske and van Reeuwijk2015a
). On the vertical and top faces of the domain we impose open boundary conditions that allow fluid to enter and leave the domain without modifying the entrainment rate of the jet (Craske & van Reeuwijk Reference Craske and van Reeuwijk2013). The approximately circular source at the base of the domain is obstructed by two narrow orthogonal strips of width
![]() ${\approx}2r_{0}/5$
whose effect is to reduce the length of the potential core (see e.g. Craske & van Reeuwijk Reference Craske and van Reeuwijk2015a
). We initiate the turbulence by applying uncorrelated perturbations of 1 % to the velocities in the first cell above the source. A constant mean scalar flux is maintained by imposing a Dirichlet boundary condition on both
${\approx}2r_{0}/5$
whose effect is to reduce the length of the potential core (see e.g. Craske & van Reeuwijk Reference Craske and van Reeuwijk2015a
). We initiate the turbulence by applying uncorrelated perturbations of 1 % to the velocities in the first cell above the source. A constant mean scalar flux is maintained by imposing a Dirichlet boundary condition on both
![]() $w$
and
$w$
and
![]() $c$
at the source.
$c$
at the source.
Data for a fully developed statistically steady jet were acquired by running simulations for a total duration of not less than
![]() $6000{\it\tau}_{0}$
, where
$6000{\it\tau}_{0}$
, where
![]() ${\it\tau}_{0}\equiv Q_{0}^{2}/M_{0}^{3/2}$
is a characteristic time scale relevant to the source. Data from the first
${\it\tau}_{0}\equiv Q_{0}^{2}/M_{0}^{3/2}$
is a characteristic time scale relevant to the source. Data from the first
![]() $3000{\it\tau}_{0}$
time units were discarded to eliminate large-scale transient behaviour, before statistics were obtained over the remaining duration of
$3000{\it\tau}_{0}$
time units were discarded to eliminate large-scale transient behaviour, before statistics were obtained over the remaining duration of
![]() $3000{\it\tau}_{0}$
. To confirm that the integral scales of the turbulent jet are not influenced by viscous effects we simulate two jets, L and H, with Reynolds numbers
$3000{\it\tau}_{0}$
. To confirm that the integral scales of the turbulent jet are not influenced by viscous effects we simulate two jets, L and H, with Reynolds numbers
![]() $\mathit{Re}\equiv 2M_{0}^{1/2}/{\it\nu}$
of 4815 and 6810 respectively. For each of these cases we impose a constant flux
$\mathit{Re}\equiv 2M_{0}^{1/2}/{\it\nu}$
of 4815 and 6810 respectively. For each of these cases we impose a constant flux
![]() $F_{0}$
of scalar at the source in order to determine the steady-state concentration statistics. To ensure that the results are independent of grid resolution we perform a simulation
$F_{0}$
of scalar at the source in order to determine the steady-state concentration statistics. To ensure that the results are independent of grid resolution we perform a simulation
![]() $\text{H}^{\ast }$
, of reduced resolution, that uses
$\text{H}^{\ast }$
, of reduced resolution, that uses
![]() $512^{2}\times 768$
computational cells, but in other respects is identical to H. In practice, dimensional parameters such as
$512^{2}\times 768$
computational cells, but in other respects is identical to H. In practice, dimensional parameters such as
![]() ${\it\nu}$
and
${\it\nu}$
and
![]() ${\it\kappa}$
are defined by specifying the dimensionless parameters
${\it\kappa}$
are defined by specifying the dimensionless parameters
![]() $\mathit{Re}$
and
$\mathit{Re}$
and
![]() $\mathit{Sc}$
, where
$\mathit{Sc}$
, where
![]() $\mathit{Sc}$
is the Schmidt number. Consequently, it is convenient to let the inlet velocity be equal to 1 and specify
$\mathit{Sc}$
is the Schmidt number. Consequently, it is convenient to let the inlet velocity be equal to 1 and specify
![]() ${\it\nu}=2M_{0}^{1/2}/\mathit{Re}$
and
${\it\nu}=2M_{0}^{1/2}/\mathit{Re}$
and
![]() ${\it\kappa}={\it\nu}/\mathit{Sc}$
. Further details of the simulations can be found in table 1.
${\it\kappa}={\it\nu}/\mathit{Sc}$
. Further details of the simulations can be found in table 1.
Table 1. Simulation details.

Azimuthally averaged data were obtained by partitioning the domain into concentric cylindrical cells and averaging over all cells lying within a given shell. Therefore, in the steady-state simulations the mean
![]() $\overline{{\it\chi}}$
of a quantity
$\overline{{\it\chi}}$
of a quantity
![]() ${\it\chi}$
is obtained from an azimuthal average, in addition to a time average, and is consequently a function of
${\it\chi}$
is obtained from an azimuthal average, in addition to a time average, and is consequently a function of
![]() $r$
and
$r$
and
![]() $z$
. To compute integrals such as
$z$
. To compute integrals such as
![]() $C_{m}$
, defined in (1.1), and the fluxes
$C_{m}$
, defined in (1.1), and the fluxes
![]() $Q_{m},M_{m},F_{m}$
and
$Q_{m},M_{m},F_{m}$
and
![]() $F_{f}$
(see § 2), we define the upper limit of integration
$F_{f}$
(see § 2), we define the upper limit of integration
![]() $r_{d}$
according to
$r_{d}$
according to
![]() $w(r_{d},z,t)=0.01\,w_{m}(z,t)$
(a similar criterion was employed in the analysis of experimental data by Kotsovinos & List Reference Kotsovinos and List1977).
$w(r_{d},z,t)=0.01\,w_{m}(z,t)$
(a similar criterion was employed in the analysis of experimental data by Kotsovinos & List Reference Kotsovinos and List1977).
During the course of the steady simulations we write a set of 16 complete three-dimensional field files to disk at time intervals of approximately
![]() $250{\it\tau}_{0}$
. These field files are used to obtain independent initial velocity conditions for the simulation of 16 statistically unsteady scalar transport simulations, which we shall refer to as U1–16. For the scalar field we impose an initial condition of zero concentration uniformly throughout the domain. An unsteady scalar transport simulation is then created by imposing a constant flux
$250{\it\tau}_{0}$
. These field files are used to obtain independent initial velocity conditions for the simulation of 16 statistically unsteady scalar transport simulations, which we shall refer to as U1–16. For the scalar field we impose an initial condition of zero concentration uniformly throughout the domain. An unsteady scalar transport simulation is then created by imposing a constant flux
![]() $F_{0}$
of scalar at the source.
$F_{0}$
of scalar at the source.
During each individual unsteady simulation, rather than outputting discretely sampled instantaneous data, a time average is taken over an interval in time that is much smaller than the characteristic time scale of the problem. Specifically, we employ a time interval not exceeding
![]() $2{\it\tau}_{0}$
, which prevents artificial smoothing of the front that time averaging would otherwise cause. In the unsteady simulations the azimuthal direction remains statistically homogeneous, which enables us to take azimuthal averages. In addition, the reliability of the statistics was further improved by performing an ensemble average over the 16 unsteady simulations. Therefore, a mean quantity
$2{\it\tau}_{0}$
, which prevents artificial smoothing of the front that time averaging would otherwise cause. In the unsteady simulations the azimuthal direction remains statistically homogeneous, which enables us to take azimuthal averages. In addition, the reliability of the statistics was further improved by performing an ensemble average over the 16 unsteady simulations. Therefore, a mean quantity
![]() $\overline{{\it\chi}}$
obtained from the unsteady simulations is a function of
$\overline{{\it\chi}}$
obtained from the unsteady simulations is a function of
![]() $r$
,
$r$
,
![]() $z$
and
$z$
and
![]() $t$
.
$t$
.
The dimensionless radial profiles of the steady scalar field
![]() $\overline{c}$
and the turbulence fluxes
$\overline{c}$
and the turbulence fluxes
![]() $\overline{u^{\prime }c^{\prime }}$
and
$\overline{u^{\prime }c^{\prime }}$
and
![]() $\overline{w^{\prime }c^{\prime }}$
are shown in figure 3. The profiles were taken from the range
$\overline{w^{\prime }c^{\prime }}$
are shown in figure 3. The profiles were taken from the range
![]() $z/r_{0}\in [28,55]$
and are convincingly self-similar. The comparison between cases L and H in figure 3 supports the view that the large-scale integral statistics are not significantly influenced by the Reynolds number, and their comparison to case
$z/r_{0}\in [28,55]$
and are convincingly self-similar. The comparison between cases L and H in figure 3 supports the view that the large-scale integral statistics are not significantly influenced by the Reynolds number, and their comparison to case
![]() $\text{H}^{\ast }$
demonstrates that the results are independent of the spatial grid resolution. For a validation of the velocity data, including Reynolds stresses and a comparison of
$\text{H}^{\ast }$
demonstrates that the results are independent of the spatial grid resolution. For a validation of the velocity data, including Reynolds stresses and a comparison of
![]() $Q_{m}$
and
$Q_{m}$
and
![]() $M_{m}$
to plume theory, the reader is referred to Craske & van Reeuwijk (Reference Craske and van Reeuwijk2015a
). From the steady-state simulation data we infer that the entrainment rate
$M_{m}$
to plume theory, the reader is referred to Craske & van Reeuwijk (Reference Craske and van Reeuwijk2015a
). From the steady-state simulation data we infer that the entrainment rate
![]() ${\it\alpha}=0.069$
, the virtual origin
${\it\alpha}=0.069$
, the virtual origin
![]() $z_{v}=-4.2\,r_{0}$
and the dimensionless fluxes
$z_{v}=-4.2\,r_{0}$
and the dimensionless fluxes
![]() ${\it\theta}_{m}=0.89$
and
${\it\theta}_{m}=0.89$
and
![]() ${\it\theta}_{f}=0.08$
. Having demonstrated that the integral statistics such as
${\it\theta}_{f}=0.08$
. Having demonstrated that the integral statistics such as
![]() $\overline{w^{\prime }c^{\prime }}$
are approximately independent of the Reynolds number
$\overline{w^{\prime }c^{\prime }}$
are approximately independent of the Reynolds number
![]() $\mathit{Re}$
, we choose to use case L at
$\mathit{Re}$
, we choose to use case L at
![]() $\mathit{Re}=4815$
, rather than case H with
$\mathit{Re}=4815$
, rather than case H with
![]() $\mathit{Re}=6810$
, to obtain the unsteady data, which ensures that the scalar field has ample resolution and that the maximum cell Péclet number,
$\mathit{Re}=6810$
, to obtain the unsteady data, which ensures that the scalar field has ample resolution and that the maximum cell Péclet number,
![]() $\max (\boldsymbol{u}\boldsymbol{\cdot }{\rm\Delta}\boldsymbol{x})/{\it\kappa}$
, for grid spacing
$\max (\boldsymbol{u}\boldsymbol{\cdot }{\rm\Delta}\boldsymbol{x})/{\it\kappa}$
, for grid spacing
![]() ${\rm\Delta}\boldsymbol{x}$
, remains small.
${\rm\Delta}\boldsymbol{x}$
, remains small.

Figure 3. Steady-state self-similar concentration statistics: (a) mean scalar concentration; (b,c) dimensionless turbulent fluxes. Here,
![]() $\overline{w^{\prime }c^{\prime }}$
corresponds to the longitudinal turbulent scalar flux and
$\overline{w^{\prime }c^{\prime }}$
corresponds to the longitudinal turbulent scalar flux and
![]() $\overline{u^{\prime }c^{\prime }}$
to the radial turbulent scalar flux.
$\overline{u^{\prime }c^{\prime }}$
to the radial turbulent scalar flux.
4. Propagation and spreading of the scalar front
4.1. Scaling
Following a step change in the source scalar flux, a disturbance in the integral concentration
![]() $C_{m}$
propagates and spreads in the longitudinal direction in the form of a front. The objective of this section is to track the front position, which we denote
$C_{m}$
propagates and spreads in the longitudinal direction in the form of a front. The objective of this section is to track the front position, which we denote
![]() $z^{\ast }(t)$
, and determine the rate at which it spreads. Figure 4 displays the scalar field at several instants in time. On the left-hand side of each panel is a vertical slice through the scalar field of a single member of the ensemble and on the right-hand side is the ensemble and azimuthally averaged scalar field. As the scalar is introduced into the domain it is mixed by the turbulent jet and transported in the positive
$z^{\ast }(t)$
, and determine the rate at which it spreads. Figure 4 displays the scalar field at several instants in time. On the left-hand side of each panel is a vertical slice through the scalar field of a single member of the ensemble and on the right-hand side is the ensemble and azimuthally averaged scalar field. As the scalar is introduced into the domain it is mixed by the turbulent jet and transported in the positive
![]() $z$
direction. At each time the scalar field has a similar form, in which the widest part of a given isoregion lies approximately midway between the origin and its leading edge in
$z$
direction. At each time the scalar field has a similar form, in which the widest part of a given isoregion lies approximately midway between the origin and its leading edge in
![]() $z$
.
$z$
.

Figure 4. Isoregions of scalar concentration
![]() $c(r,z,t=t_{i})$
, at times
$c(r,z,t=t_{i})$
, at times
![]() $t_{i}/{\it\tau}_{0}\approx 37\text{i},~i=1\ldots 8$
(a–h), where
$t_{i}/{\it\tau}_{0}\approx 37\text{i},~i=1\ldots 8$
(a–h), where
![]() $\mathit{Re}=4815$
. Left-hand side: instantaneous radial slice; right-hand side: azimuthal and ensemble average.
$\mathit{Re}=4815$
. Left-hand side: instantaneous radial slice; right-hand side: azimuthal and ensemble average.
A robust criterion for identifying the location of the scalar front is to define
![]() $z^{\ast }$
implicitly as
$z^{\ast }$
implicitly as
where
![]() $F_{m}^{\ast }\equiv F_{m0}/2$
is the arithmetic mean of the mean steady-state scalar flux
$F_{m}^{\ast }\equiv F_{m0}/2$
is the arithmetic mean of the mean steady-state scalar flux
![]() $F_{m0}$
before and after the step change. The value of
$F_{m0}$
before and after the step change. The value of
![]() $F_{m0}$
was obtained from steady-state data by averaging
$F_{m0}$
was obtained from steady-state data by averaging
![]() $F_{m}(z)$
over the interval
$F_{m}(z)$
over the interval
![]() $z/r_{0}\in [28,55]$
, and is slightly lower than
$z/r_{0}\in [28,55]$
, and is slightly lower than
![]() $F_{0}$
due to the contribution from the turbulent scalar flux (i.e.
$F_{0}$
due to the contribution from the turbulent scalar flux (i.e.
![]() $F_{0}=F_{m}+F_{f}$
). In addition, we define the positions
$F_{0}=F_{m}+F_{f}$
). In addition, we define the positions
![]() $z_{1/4}(t)$
and
$z_{1/4}(t)$
and
![]() $z_{3/4}(t)$
, which correspond to the longitudinal distances at which
$z_{3/4}(t)$
, which correspond to the longitudinal distances at which
![]() $F_{m}=F_{m0}/4$
and
$F_{m}=F_{m0}/4$
and
![]() $F_{m}=3F_{m0}/4$
respectively, and will allow us to quantify the longitudinal spread of the scalar.
$F_{m}=3F_{m0}/4$
respectively, and will allow us to quantify the longitudinal spread of the scalar.
Figure 5 shows typical profiles of
![]() $C_{m}$
and
$C_{m}$
and
![]() $F_{m}$
obtained from the ensemble-averaged simulation data, with circles marking the location of the front
$F_{m}$
obtained from the ensemble-averaged simulation data, with circles marking the location of the front
![]() $z^{\ast }$
. In the region
$z^{\ast }$
. In the region
![]() $r_{0}\ll z\ll z^{\ast }$
the concentration field is in a quasi-steady state and the integral concentration
$r_{0}\ll z\ll z^{\ast }$
the concentration field is in a quasi-steady state and the integral concentration
![]() $C_{m}$
increases linearly in
$C_{m}$
increases linearly in
![]() $z$
to a maximum behind the front (figure 5
a). Ahead of its maximum,
$z$
to a maximum behind the front (figure 5
a). Ahead of its maximum,
![]() $C_{m}$
tends to zero smoothly with increasing
$C_{m}$
tends to zero smoothly with increasing
![]() $z/z^{\ast }$
. It is observed that the propagation speed of the front decreases with increasing
$z/z^{\ast }$
. It is observed that the propagation speed of the front decreases with increasing
![]() $t$
. Evident in the behaviour of both
$t$
. Evident in the behaviour of both
![]() $C_{m}$
and
$C_{m}$
and
![]() $F_{m}$
is that the longitudinal extent of the front increases in time, which indicates the presence of some form of longitudinal mixing.
$F_{m}$
is that the longitudinal extent of the front increases in time, which indicates the presence of some form of longitudinal mixing.

Figure 5. Profiles of (a) the integral concentration
![]() $C_{m}$
and (b) the integral flux
$C_{m}$
and (b) the integral flux
![]() $F_{m}$
against
$F_{m}$
against
![]() $z/r_{0}$
, at times
$z/r_{0}$
, at times
![]() $t_{i}/{\it\tau}_{0}\approx 37\text{i},i=1\ldots 5$
, with the position of the front
$t_{i}/{\it\tau}_{0}\approx 37\text{i},i=1\ldots 5$
, with the position of the front
![]() $z^{\ast }/r_{0}$
(○) and the limits of the longitudinal spread of the front
$z^{\ast }/r_{0}$
(○) and the limits of the longitudinal spread of the front
![]() $z_{1/4}/r_{0}$
(▵) and
$z_{1/4}/r_{0}$
(▵) and
![]() $z_{3/4}/r_{0}$
(▿). The thin line in (b) denotes the function
$z_{3/4}/r_{0}$
(▿). The thin line in (b) denotes the function
![]() $\text{erfc}[(z-z^{\ast })/{\it\sigma}]$
.
$\text{erfc}[(z-z^{\ast })/{\it\sigma}]$
.
Due to the fact that the velocity in the jet
![]() $w_{m}\sim 1/z$
, one expects disturbances to propagate according to
$w_{m}\sim 1/z$
, one expects disturbances to propagate according to
![]() $z^{\ast }\sim \sqrt{t}$
. To investigate this we plot
$z^{\ast }\sim \sqrt{t}$
. To investigate this we plot
![]() $(z^{\ast }-z_{v})^{2}$
against
$(z^{\ast }-z_{v})^{2}$
against
![]() $t-t_{v}$
in figure 6, where
$t-t_{v}$
in figure 6, where
![]() $t_{v}$
can be regarded as the location of the virtual source in time. Using the steady-state value of
$t_{v}$
can be regarded as the location of the virtual source in time. Using the steady-state value of
![]() $z_{v}$
,
$z_{v}$
,
![]() $t_{v}=-1.5{\it\tau}_{0}$
was obtained by fitting a straight line to
$t_{v}=-1.5{\it\tau}_{0}$
was obtained by fitting a straight line to
![]() $(z-z_{v})^{2}$
, whose agreement with the simulation data in figure 6 confirms the expected scaling relation. Both
$(z-z_{v})^{2}$
, whose agreement with the simulation data in figure 6 confirms the expected scaling relation. Both
![]() $z_{v}/r_{0}$
and
$z_{v}/r_{0}$
and
![]() $t_{v}/{\it\tau}_{0}$
are small in comparison to the size of the domain and the total duration of the simulations respectively, and consequently play an insignificant role in the far-field scaling observed in figure 6. Interestingly,
$t_{v}/{\it\tau}_{0}$
are small in comparison to the size of the domain and the total duration of the simulations respectively, and consequently play an insignificant role in the far-field scaling observed in figure 6. Interestingly,
![]() $z^{\ast }\sim \sqrt{t}$
corresponds to the classical dispersion scaling, although for planar jets and plumes, for example, in which
$z^{\ast }\sim \sqrt{t}$
corresponds to the classical dispersion scaling, although for planar jets and plumes, for example, in which ![]() , one would expect to find a different power-law scaling. It is noteworthy that the propagation rate of the front appears to be slightly greater than
, one would expect to find a different power-law scaling. It is noteworthy that the propagation rate of the front appears to be slightly greater than
![]() $w_{m}$
(figure 6, dashed line). Furthermore, from figure 6,
$w_{m}$
(figure 6, dashed line). Furthermore, from figure 6,
![]() $z_{1/4}$
and
$z_{1/4}$
and
![]() $z_{3/4}$
can be seen to scale in proportion to
$z_{3/4}$
can be seen to scale in proportion to
![]() $\sqrt{t}$
, which suggests that the scaling associated with the position of the front is identical to that associated with its longitudinal rate of spread, and that the process is therefore self-similar.
$\sqrt{t}$
, which suggests that the scaling associated with the position of the front is identical to that associated with its longitudinal rate of spread, and that the process is therefore self-similar.

Figure 6. Position of the scalar front (○) and corresponding linear fit (solid line), compared with the ‘top-hat’ propagation
![]() $w_{m}$
(dashed line). The approximate extent of the front is indicated by
$w_{m}$
(dashed line). The approximate extent of the front is indicated by
![]() $z_{1/4}(t)$
(▵) and
$z_{1/4}(t)$
(▵) and
![]() $z_{3/4}(t)$
(▿). The region between the two vertical dotted lines corresponds to the time domain that was used to obtain averaged properties of the front and the self-similar profiles that are shown in figures 7–9.
$z_{3/4}(t)$
(▿). The region between the two vertical dotted lines corresponds to the time domain that was used to obtain averaged properties of the front and the self-similar profiles that are shown in figures 7–9.

Figure 7. (a) Self-similar profiles of
![]() $C_{m}$
for fixed times (grey) and their average (black); (b) normalised profiles of scalar concentration
$C_{m}$
for fixed times (grey) and their average (black); (b) normalised profiles of scalar concentration
![]() $\overline{c}/c_{c}$
; (c) normalised profiles of mean scalar flux
$\overline{c}/c_{c}$
; (c) normalised profiles of mean scalar flux
![]() $\overline{w}\,\overline{c}/w_{c}c_{c}$
; (d) normalised profiles of turbulent scalar flux
$\overline{w}\,\overline{c}/w_{c}c_{c}$
; (d) normalised profiles of turbulent scalar flux
![]() $\overline{w^{\prime }c^{\prime }}/w_{c}c_{c}$
. The variables
$\overline{w^{\prime }c^{\prime }}/w_{c}c_{c}$
. The variables
![]() $w_{c}$
and
$w_{c}$
and
![]() $c_{c}$
are the centreline longitudinal velocity and concentration respectively. In (a–d) the positions
$c_{c}$
are the centreline longitudinal velocity and concentration respectively. In (a–d) the positions
![]() $z_{1/4}$
,
$z_{1/4}$
,
![]() $z^{\ast }$
and
$z^{\ast }$
and
![]() $z_{3/4}$
are marked with ▵, ○ and ▿ respectively. The profiles displayed in (b–d) were obtained from a moving average at either
$z_{3/4}$
are marked with ▵, ○ and ▿ respectively. The profiles displayed in (b–d) were obtained from a moving average at either
![]() $z_{1/4},z^{\ast }$
or
$z_{1/4},z^{\ast }$
or
![]() $z_{3/4}$
, over the time domain indicated in figure 6.
$z_{3/4}$
, over the time domain indicated in figure 6.
The scalar is released continuously at the source with a constant source flux
![]() $F_{0}$
, therefore
$F_{0}$
, therefore
Since
![]() $C_{m}\propto z$
in the steady state, we conclude that we can normalise the profiles of
$C_{m}\propto z$
in the steady state, we conclude that we can normalise the profiles of
![]() $C_{m}$
by
$C_{m}$
by
![]() $F_{m}^{\ast }t/z^{\ast }$
in order to observe self-similarity. Profiles of
$F_{m}^{\ast }t/z^{\ast }$
in order to observe self-similarity. Profiles of
![]() $C_{m}$
normalised in this way, plotted against the normalised streamwise coordinate
$C_{m}$
normalised in this way, plotted against the normalised streamwise coordinate
![]() $z/z^{\ast }$
, are shown in figure 7(a). The approximate collapse indicates that, following a step change in the flux of concentration at the source, the transport of a passive scalar in a jet is indeed a self-similar process that can be described by the variable
$z/z^{\ast }$
, are shown in figure 7(a). The approximate collapse indicates that, following a step change in the flux of concentration at the source, the transport of a passive scalar in a jet is indeed a self-similar process that can be described by the variable
![]() $z/z^{\ast }$
.
$z/z^{\ast }$
.
4.2. Longitudinal mixing
To quantify the mixing at the front, we fit the data in figure 5(b) to a function of the form
![]() $F_{m}/F_{m}^{\ast }=\text{erfc}[(z-z^{\ast }(t))/{\it\sigma}]$
. This choice is motivated by the fact that it provides a good approximation to the solution of an advection–diffusion equation if it is assumed that the characteristic velocity in the vicinity of the front is approximately constant. The longitudinal spread of the scalar flux
$F_{m}/F_{m}^{\ast }=\text{erfc}[(z-z^{\ast }(t))/{\it\sigma}]$
. This choice is motivated by the fact that it provides a good approximation to the solution of an advection–diffusion equation if it is assumed that the characteristic velocity in the vicinity of the front is approximately constant. The longitudinal spread of the scalar flux
![]() ${\it\sigma}(t)=\sqrt{2D_{e}t}$
and
${\it\sigma}(t)=\sqrt{2D_{e}t}$
and
![]() $D_{e}$
is an effective mixing coefficient. The error function is indicated with a thin line in figure 5(b) and exhibits an excellent agreement with the simulation data. From the definition of the longitudinal positions
$D_{e}$
is an effective mixing coefficient. The error function is indicated with a thin line in figure 5(b) and exhibits an excellent agreement with the simulation data. From the definition of the longitudinal positions
![]() $z_{1/4}$
and
$z_{1/4}$
and
![]() $z_{3/4}$
, which represent percentiles of
$z_{3/4}$
, which represent percentiles of
![]() $F_{m}$
, we infer
$F_{m}$
, we infer
![]() ${\it\sigma}=1.048(z_{1/4}-z_{3/4})$
. The fit allows us to calculate an average mixing coefficient
${\it\sigma}=1.048(z_{1/4}-z_{3/4})$
. The fit allows us to calculate an average mixing coefficient
![]() $D_{e}=0.74M_{m}^{1/2}$
. In an effort to account for the observed level of mixing, we assume that the turbulent Schmidt number is approximately unity and compare the value of
$D_{e}=0.74M_{m}^{1/2}$
. In an effort to account for the observed level of mixing, we assume that the turbulent Schmidt number is approximately unity and compare the value of
![]() $D_{e}$
with the uniform turbulent viscosity
$D_{e}$
with the uniform turbulent viscosity
![]() ${\it\nu}_{T}$
obtained from a gradient-diffusion hypothesis. Based on the measurements of Hussein, Capp & George (Reference Hussein, Capp and George1994), Pope (Reference Pope2000) reports that in jets
${\it\nu}_{T}$
obtained from a gradient-diffusion hypothesis. Based on the measurements of Hussein, Capp & George (Reference Hussein, Capp and George1994), Pope (Reference Pope2000) reports that in jets
![]() ${\it\nu}_{T}\approx 0.033\,M_{m}^{1/2}$
. (More precisely, Pope (Reference Pope2000) expresses
${\it\nu}_{T}\approx 0.033\,M_{m}^{1/2}$
. (More precisely, Pope (Reference Pope2000) expresses
![]() ${\it\nu}_{T}$
in terms of the centreline velocity
${\it\nu}_{T}$
in terms of the centreline velocity
![]() $w_{c}$
and the radial location
$w_{c}$
and the radial location
![]() $r_{1/2}$
at which
$r_{1/2}$
at which
![]() $\overline{w}=w_{c}/2$
(the jet half-width) as
$\overline{w}=w_{c}/2$
(the jet half-width) as
![]() ${\it\nu}_{T}\approx 0.028\,w_{c}r_{1/2}$
. In a Gaussian jet
${\it\nu}_{T}\approx 0.028\,w_{c}r_{1/2}$
. In a Gaussian jet
![]() $w_{c}=2w_{m}$
and
$w_{c}=2w_{m}$
and
![]() $r_{1/2}=\sqrt{\ln 2/2}\,r_{m}$
, hence
$r_{1/2}=\sqrt{\ln 2/2}\,r_{m}$
, hence
![]() ${\it\nu}_{T}\approx 0.033\,w_{m}r_{m}$
.) The significant difference between this estimation and
${\it\nu}_{T}\approx 0.033\,w_{m}r_{m}$
.) The significant difference between this estimation and
![]() $D_{e}$
implies that turbulence alone cannot account for the mixing observed at the front. An intuitive way of understanding the difference between
$D_{e}$
implies that turbulence alone cannot account for the mixing observed at the front. An intuitive way of understanding the difference between
![]() ${\it\nu}_{T}$
and
${\it\nu}_{T}$
and
![]() $D_{e}$
is that it implies that the longitudinal extent of the front (determined by
$D_{e}$
is that it implies that the longitudinal extent of the front (determined by
![]() $D_{e}$
) exceeds the radius of the jet (determined by
$D_{e}$
) exceeds the radius of the jet (determined by
![]() ${\it\nu}_{T}$
). We will demonstrate that shear-flow dispersion accounts for the difference by examining the way in which the concentration profile is distorted in the vicinity of the front.
${\it\nu}_{T}$
). We will demonstrate that shear-flow dispersion accounts for the difference by examining the way in which the concentration profile is distorted in the vicinity of the front.
As described in § 1, longitudinal mixing of an integral quantity such as
![]() $C_{m}$
can occur due to a uniform increase in
$C_{m}$
can occur due to a uniform increase in
![]() $\overline{w^{\prime }c^{\prime }}$
over the radius of the jet (turbulent mixing) or due to a distortion of the mean concentration profile
$\overline{w^{\prime }c^{\prime }}$
over the radius of the jet (turbulent mixing) or due to a distortion of the mean concentration profile
![]() $\overline{c}$
(shear-flow dispersion). Shear-flow dispersion results in a local increase in the correlation
$\overline{c}$
(shear-flow dispersion). Shear-flow dispersion results in a local increase in the correlation
![]() $\langle \overline{w}\,\overline{c}\rangle$
, involving only mean-flow quantities, and therefore in a local increase in the mean scalar flux. It is therefore appropriate to examine radial profiles of
$\langle \overline{w}\,\overline{c}\rangle$
, involving only mean-flow quantities, and therefore in a local increase in the mean scalar flux. It is therefore appropriate to examine radial profiles of
![]() $\overline{c}$
and
$\overline{c}$
and
![]() $\overline{w}$
in the vicinity of the front, which are shown alongside the fluxes
$\overline{w}$
in the vicinity of the front, which are shown alongside the fluxes
![]() $\overline{w}\,\overline{c}$
and
$\overline{w}\,\overline{c}$
and
![]() $\overline{w^{\prime }c^{\prime }}$
in figure 7. The profiles displayed in figure 7(b–d) are normalised using centreline values
$\overline{w^{\prime }c^{\prime }}$
in figure 7. The profiles displayed in figure 7(b–d) are normalised using centreline values
![]() $c_{c}(z,t)\equiv \overline{c}(0,z,t)$
and
$c_{c}(z,t)\equiv \overline{c}(0,z,t)$
and
![]() $w_{c}(z)\equiv \overline{w}(0,z)$
of the mean concentration and the mean longitudinal velocity respectively. The central observation that can be made from figure 7(b–d) is that as
$w_{c}(z)\equiv \overline{w}(0,z)$
of the mean concentration and the mean longitudinal velocity respectively. The central observation that can be made from figure 7(b–d) is that as
![]() $z/z^{\ast }$
increases the profiles become narrower. The scalar is transported by advection to regions of relatively large
$z/z^{\ast }$
increases the profiles become narrower. The scalar is transported by advection to regions of relatively large
![]() $z/z^{\ast }$
when it is located close to the centreline of the jet, where the longitudinal velocities are highest. Consequently, the scalar profile becomes more peaked with downstream distance, which is evident in figure 7(b). Figure 7(c,d) shows that the turbulent flux does not scale in exact proportion to the mean flux in the vicinity of the front. Rather, the turbulent flux appears to increase at large values of
$z/z^{\ast }$
when it is located close to the centreline of the jet, where the longitudinal velocities are highest. Consequently, the scalar profile becomes more peaked with downstream distance, which is evident in figure 7(b). Figure 7(c,d) shows that the turbulent flux does not scale in exact proportion to the mean flux in the vicinity of the front. Rather, the turbulent flux appears to increase at large values of
![]() $z/z^{\ast }$
, although it continues to make a relatively small contribution to the total flux.
$z/z^{\ast }$
, although it continues to make a relatively small contribution to the total flux.
To quantify precisely the relative contribution to the total scalar flux made by the mean and turbulent flow, we plot the dimensionless scalar fluxes
![]() ${\it\theta}_{m}$
and
${\it\theta}_{m}$
and
![]() ${\it\theta}_{f}$
respectively with respect to the normalised downstream distance in figure 8. The grey curves displayed in figure 8 correspond to different times and exhibit an approximate collapse with respect to the variable
${\it\theta}_{f}$
respectively with respect to the normalised downstream distance in figure 8. The grey curves displayed in figure 8 correspond to different times and exhibit an approximate collapse with respect to the variable
![]() $z/z^{\ast }$
, which is consistent with the self-similarity that was described in § 4.1. In the steady state the radial dependence of the velocity and concentration profiles is approximately independent of
$z/z^{\ast }$
, which is consistent with the self-similarity that was described in § 4.1. In the steady state the radial dependence of the velocity and concentration profiles is approximately independent of
![]() $z$
, which implies that
$z$
, which implies that
![]() ${\it\theta}_{m}$
is constant. Consequently, shear-flow dispersion is evident as a departure from the steady-state value of
${\it\theta}_{m}$
is constant. Consequently, shear-flow dispersion is evident as a departure from the steady-state value of
![]() ${\it\theta}_{m}$
and is seen in figure 8 to be significant over a large extent of the
${\it\theta}_{m}$
and is seen in figure 8 to be significant over a large extent of the
![]() $z/z^{\ast }$
domain. Figure 8 also indicates that in a quasi-steady state, for which
$z/z^{\ast }$
domain. Figure 8 also indicates that in a quasi-steady state, for which
![]() $z/z^{\ast }\ll 1$
, the contribution of the dimensionless turbulent flux (
$z/z^{\ast }\ll 1$
, the contribution of the dimensionless turbulent flux (
![]() ${\it\theta}_{f}$
) amounts to the expected 10 %, but rises to 20 % at the front, where
${\it\theta}_{f}$
) amounts to the expected 10 %, but rises to 20 % at the front, where
![]() $z=z^{\ast }$
.
$z=z^{\ast }$
.

Figure 8. Evolution of the dimensionless mean scalar flux
![]() ${\it\theta}_{m}$
and the turbulent scalar flux
${\it\theta}_{m}$
and the turbulent scalar flux
![]() ${\it\theta}_{f}$
. Each grey line corresponds to the behaviour of
${\it\theta}_{f}$
. Each grey line corresponds to the behaviour of
![]() ${\it\theta}$
at a fixed point in time, while the solid black line corresponds to their average, obtained over the time domain indicated in figure 6. The dashed line denotes the total dimensionless flux
${\it\theta}$
at a fixed point in time, while the solid black line corresponds to their average, obtained over the time domain indicated in figure 6. The dashed line denotes the total dimensionless flux
![]() ${\it\theta}_{m}+{\it\theta}_{f}$
and the circles the prediction based on the model (see (5.8)).
${\it\theta}_{m}+{\it\theta}_{f}$
and the circles the prediction based on the model (see (5.8)).
Figure 8 confirms that in the vicinity of
![]() $z=z^{\ast }$
the local distortion of the concentration profile
$z=z^{\ast }$
the local distortion of the concentration profile
![]() $\overline{c}$
, evident in figure 7(b), acts in correlation with
$\overline{c}$
, evident in figure 7(b), acts in correlation with
![]() $\overline{w}$
to increase the dimensionless scalar flux
$\overline{w}$
to increase the dimensionless scalar flux
![]() ${\it\theta}_{m}$
. In particular, the dimensionless scalar flux ranges from approximately 1.0 (for
${\it\theta}_{m}$
. In particular, the dimensionless scalar flux ranges from approximately 1.0 (for
![]() $z/z^{\ast }\ll 1$
) to 2.0. It is also evident that
$z/z^{\ast }\ll 1$
) to 2.0. It is also evident that
![]() ${\it\theta}_{f}$
increases in the vicinity of
${\it\theta}_{f}$
increases in the vicinity of
![]() $z=z^{\ast }$
. Indeed, since
$z=z^{\ast }$
. Indeed, since
![]() ${\it\theta}_{f}$
is an integral quantity, in addition to accounting for a local increase in the magnitude of the turbulent flux
${\it\theta}_{f}$
is an integral quantity, in addition to accounting for a local increase in the magnitude of the turbulent flux
![]() $\overline{w^{\prime }c^{\prime }}$
(see figure 7
d), it accounts for a narrowing of the spatial distribution of
$\overline{w^{\prime }c^{\prime }}$
(see figure 7
d), it accounts for a narrowing of the spatial distribution of
![]() $c^{\prime }$
. Hence, it is to be expected that the behaviours of
$c^{\prime }$
. Hence, it is to be expected that the behaviours of
![]() ${\it\theta}_{m}$
and
${\it\theta}_{m}$
and
![]() ${\it\theta}_{f}$
share similar features. We attribute the fact that
${\it\theta}_{f}$
share similar features. We attribute the fact that
![]() ${\it\theta}_{f}$
does not appear to remain in constant proportion to
${\it\theta}_{f}$
does not appear to remain in constant proportion to
![]() ${\it\theta}_{m}$
to the relatively small increase in the magnitude of the turbulent flux
${\it\theta}_{m}$
to the relatively small increase in the magnitude of the turbulent flux
![]() $\overline{w^{\prime }c^{\prime }}$
. It should be noted that beyond
$\overline{w^{\prime }c^{\prime }}$
. It should be noted that beyond
![]() $z/z^{\ast }$
, the fluxes
$z/z^{\ast }$
, the fluxes
![]() $\overline{w}\,\overline{c}$
,
$\overline{w}\,\overline{c}$
,
![]() $\overline{w^{\prime }c^{\prime }}$
and the concentration
$\overline{w^{\prime }c^{\prime }}$
and the concentration
![]() $C_{m}$
used in their normalisation approach zero, which makes it difficult to obtain an accurate estimation of
$C_{m}$
used in their normalisation approach zero, which makes it difficult to obtain an accurate estimation of
![]() ${\it\theta}_{f}$
and
${\it\theta}_{f}$
and
![]() ${\it\theta}_{m}$
from a finite dataset.
${\it\theta}_{m}$
from a finite dataset.
As pointed out previously, fluid located close to
![]() $r=0$
is transported by relatively high longitudinal velocities, and can therefore propagate further than fluid located at the periphery of the jet. It is therefore natural that at large distances from the source one sees a narrowing of the scalar distribution (see figure 7
b). At the leading edge of the scalar field, we can therefore expect the scalar profile to take the form of a spike at
$r=0$
is transported by relatively high longitudinal velocities, and can therefore propagate further than fluid located at the periphery of the jet. It is therefore natural that at large distances from the source one sees a narrowing of the scalar distribution (see figure 7
b). At the leading edge of the scalar field, we can therefore expect the scalar profile to take the form of a spike at
![]() $r=0$
. For a Gaussian velocity profile, the largest velocity is found on the centreline and has a value of
$r=0$
. For a Gaussian velocity profile, the largest velocity is found on the centreline and has a value of
![]() $2w_{m}$
, which implies an upper bound of
$2w_{m}$
, which implies an upper bound of
![]() ${\it\theta}_{m}=2$
. Hence, the mean scalar flux
${\it\theta}_{m}=2$
. Hence, the mean scalar flux
![]() $F_{m}$
cannot exceed
$F_{m}$
cannot exceed
![]() $2C_{m}w_{m}$
. Furthermore, if it is assumed that
$2C_{m}w_{m}$
. Furthermore, if it is assumed that
![]() $\text{d}z^{\ast }/\text{d}t\approx w_{m}(z^{\ast })\propto 1/z^{\ast }$
, in accordance with figure 6, then fluid on the jet centreline will reach
$\text{d}z^{\ast }/\text{d}t\approx w_{m}(z^{\ast })\propto 1/z^{\ast }$
, in accordance with figure 6, then fluid on the jet centreline will reach
![]() $z/z^{\ast }\approx \sqrt{2}$
. At
$z/z^{\ast }\approx \sqrt{2}$
. At
![]() $z/z^{\ast }\approx \sqrt{2}$
in figure 8 we observe that the sum
$z/z^{\ast }\approx \sqrt{2}$
in figure 8 we observe that the sum
![]() ${\it\theta}_{m}+{\it\theta}_{f}\approx 2$
. For
${\it\theta}_{m}+{\it\theta}_{f}\approx 2$
. For
![]() $z/z^{\ast }>\sqrt{2}$
, we see a reduction in
$z/z^{\ast }>\sqrt{2}$
, we see a reduction in
![]() ${\it\theta}_{f}$
and that
${\it\theta}_{f}$
and that
![]() ${\it\theta}_{m}$
approaches a value of 2, as expected.
${\it\theta}_{m}$
approaches a value of 2, as expected.
5. A model for shear-flow dispersion in jets
Although shear-flow dispersion was originally developed for pipe flow (Taylor Reference Taylor1953, Reference Taylor1954b ), Craske & van Reeuwijk (Reference Craske and van Reeuwijk2015b ) demonstrated that it could be usefully extended to boundary-free shear flow, such as a jet. In this section we will summarise the key features of the approach and obtain a model for the dispersion of a passive scalar. In contrast to a jet, the steady-state distribution of a scalar in a pipe is uniform and bounded in the radial direction. Like jets, however, both the velocity distribution and the scalar distribution are self-similar, which means that their radial dependence is invariant in the longitudinal direction. Fundamental to both dispersion in pipe flow and dispersion in jets is the idea that changes in the mean scalar concentration in the longitudinal direction can cause a local departure from self-similarity over the lateral (radial) dimension. Specifically, the departure from self-similarity in the scalar is caused by lateral gradients in the longitudinal velocity and, in correlation with the longitudinal velocity, results in a local increase in the scalar flux.
Taylor demonstrated that, to leading order, the radial dependence of the modification to the uniform concentration is independent of the longitudinal coordinate. Consequently, one can define a dimensionless function
![]() $g_{1}({\it\eta})$
to describe the shape of the perturbed concentration profile, where
$g_{1}({\it\eta})$
to describe the shape of the perturbed concentration profile, where
![]() ${\it\eta}\equiv r/r_{m}$
. Using this notation, the basic dimensionless steady-state concentration will be denoted
${\it\eta}\equiv r/r_{m}$
. Using this notation, the basic dimensionless steady-state concentration will be denoted
![]() $g_{0}({\it\eta})$
. The functions
$g_{0}({\it\eta})$
. The functions
![]() $g_{0}$
and
$g_{0}$
and
![]() $g_{1}$
apply equally well to the analysis of pipe flow and jet flow, although for pipe flow the steady-state scalar concentration is constant, and therefore
$g_{1}$
apply equally well to the analysis of pipe flow and jet flow, although for pipe flow the steady-state scalar concentration is constant, and therefore
![]() $g_{0}$
does not depend on
$g_{0}$
does not depend on
![]() ${\it\eta}$
. The aim is to establish an expression for the dimensionless concentration
${\it\eta}$
. The aim is to establish an expression for the dimensionless concentration
where
![]() $L_{1}$
determines the degree to which the concentration profile departs from a steady state, and is therefore expected to depend in some way on the behaviour of the scalar in the longitudinal direction. Evidently, if the dimensionless velocity profile
$L_{1}$
determines the degree to which the concentration profile departs from a steady state, and is therefore expected to depend in some way on the behaviour of the scalar in the longitudinal direction. Evidently, if the dimensionless velocity profile
![]() $\overline{w}/w_{m}=f_{0}({\it\eta})$
is known, (5.1) can be multiplied by
$\overline{w}/w_{m}=f_{0}({\it\eta})$
is known, (5.1) can be multiplied by
![]() $f_{0}$
and integrated with respect to
$f_{0}$
and integrated with respect to
![]() ${\it\eta}^{2}$
(i.e. over a lateral slice of the pipe flow or jet). The resulting integral corresponds to the dimensionless flux
${\it\eta}^{2}$
(i.e. over a lateral slice of the pipe flow or jet). The resulting integral corresponds to the dimensionless flux
![]() ${\it\theta}_{m}\equiv F_{m}/(w_{m}C_{m})$
:
${\it\theta}_{m}\equiv F_{m}/(w_{m}C_{m})$
:
We define
![]() ${\it\theta}_{0}\equiv \langle f_{0}g_{0}\rangle$
as the dimensionless steady-state scalar flux, and
${\it\theta}_{0}\equiv \langle f_{0}g_{0}\rangle$
as the dimensionless steady-state scalar flux, and
![]() ${\it\theta}_{1}\equiv \langle f_{0}g_{1}\rangle$
as the additional flux arising from changes in the shape of
${\it\theta}_{1}\equiv \langle f_{0}g_{1}\rangle$
as the additional flux arising from changes in the shape of
![]() $g({\it\eta})$
. Here, the operator
$g({\it\eta})$
. Here, the operator
![]() $\langle \,\rangle$
is a suitable non-vanishing spatial average over
$\langle \,\rangle$
is a suitable non-vanishing spatial average over
![]() ${\it\eta}$
, which for jets we define in § 5.2. The ultimate aim of a dispersion closure is to obtain an expression for
${\it\eta}$
, which for jets we define in § 5.2. The ultimate aim of a dispersion closure is to obtain an expression for
![]() ${\it\theta}_{m}$
in terms of the integral concentration
${\it\theta}_{m}$
in terms of the integral concentration
![]() $C_{m}$
and its longitudinal derivatives.
$C_{m}$
and its longitudinal derivatives.
Instead of working with the ensemble average scalar concentration
![]() $\overline{c}$
, Craske & van Reeuwijk (Reference Craske and van Reeuwijk2015b
) worked with the dimensionless concentration
$\overline{c}$
, Craske & van Reeuwijk (Reference Craske and van Reeuwijk2015b
) worked with the dimensionless concentration
where
![]() $c_{m0}(z)$
is the mean steady-state concentration and
$c_{m0}(z)$
is the mean steady-state concentration and
![]() $\mathscr{C}_{m}\equiv c_{m}/c_{m0}$
. Consequently, in the steady state
$\mathscr{C}_{m}\equiv c_{m}/c_{m0}$
. Consequently, in the steady state
![]() $\mathscr{C}$
is independent of
$\mathscr{C}$
is independent of
![]() $z$
in both jets and pipes, making it possible to recast Taylor’s approach to dispersion in pipe flow in a form that is applicable to jets. In the following sections we will substitute (5.3) into the longitudinal scalar transport equation to relate the unknown perturbed profile
$z$
in both jets and pipes, making it possible to recast Taylor’s approach to dispersion in pipe flow in a form that is applicable to jets. In the following sections we will substitute (5.3) into the longitudinal scalar transport equation to relate the unknown perturbed profile
![]() $g_{1}$
to
$g_{1}$
to
![]() $\partial _{z}\mathscr{C}_{m}$
.
$\partial _{z}\mathscr{C}_{m}$
.
5.1. Shear-flow dispersion in a pipe
To begin, we describe the classical dispersion problem in a pipe flow using the notation described above. To understand the evolution of a step change in scalar concentration in a pipe of uniform radius
![]() $r_{m}$
, Taylor employed a frame of reference moving with the mean velocity
$r_{m}$
, Taylor employed a frame of reference moving with the mean velocity
![]() $\langle \overline{w}\rangle =w_{m}$
. For pipes, for which
$\langle \overline{w}\rangle =w_{m}$
. For pipes, for which
![]() ${\it\theta}_{0}=1$
, as the steady-state concentration is uniform, this coordinate transformation ensures that the equation governing the cross-sectional average concentration does not contain mean flux terms. More generally, it is necessary to move at the velocity associated with the steady-state scalar flux
${\it\theta}_{0}=1$
, as the steady-state concentration is uniform, this coordinate transformation ensures that the equation governing the cross-sectional average concentration does not contain mean flux terms. More generally, it is necessary to move at the velocity associated with the steady-state scalar flux
![]() $w_{m}{\it\theta}_{0}$
to eliminate the mean flux terms. Taylor subtracted from the governing equation for scalar transport the evolution equation for the cross-sectional average concentration, and found, for large times, a leading-order balance between radial transport of the perturbed scalar profile and longitudinal advection (see appendix A for details):
$w_{m}{\it\theta}_{0}$
to eliminate the mean flux terms. Taylor subtracted from the governing equation for scalar transport the evolution equation for the cross-sectional average concentration, and found, for large times, a leading-order balance between radial transport of the perturbed scalar profile and longitudinal advection (see appendix A for details):
where
![]() ${\it\kappa}_{T}$
is the eddy diffusivity. In particular, (5.4) shows that the longitudinal gradient of the dimensionless average concentration
${\it\kappa}_{T}$
is the eddy diffusivity. In particular, (5.4) shows that the longitudinal gradient of the dimensionless average concentration
![]() $\mathscr{C}_{m}$
provides the forcing for the perturbation in the concentration profile
$\mathscr{C}_{m}$
provides the forcing for the perturbation in the concentration profile
![]() $L_{1}g_{1}$
. The separable form of (5.4) allows one to infer that
$L_{1}g_{1}$
. The separable form of (5.4) allows one to infer that
to within an arbitrary multiplicative constant, if it is assumed that
![]() ${\it\kappa}_{T}$
does not depend on
${\it\kappa}_{T}$
does not depend on
![]() ${\it\eta}$
. Equations (5.4) and (5.5) demonstrate that the amplitude of the scalar perturbation is proportional to the longitudinal gradient of the dimensionless concentration, and that
${\it\eta}$
. Equations (5.4) and (5.5) demonstrate that the amplitude of the scalar perturbation is proportional to the longitudinal gradient of the dimensionless concentration, and that
![]() $g_{1}$
, and therefore
$g_{1}$
, and therefore
![]() ${\it\theta}_{1}$
, can, in principle, be determined a priori by solving an ordinary differential equation when
${\it\theta}_{1}$
, can, in principle, be determined a priori by solving an ordinary differential equation when
![]() $f_{0}$
is known.
$f_{0}$
is known.
5.2. Shear-flow dispersion in an axisymmetric jet
To apply Taylor’s dispersion theory to jets we assume that the decomposition
![]() $\mathscr{C}=\mathscr{C}_{m}(g_{0}+L_{1}g_{1})$
provides a leading-order representation of the dimensionless concentration field. The use of the normalised radius
$\mathscr{C}=\mathscr{C}_{m}(g_{0}+L_{1}g_{1})$
provides a leading-order representation of the dimensionless concentration field. The use of the normalised radius
![]() ${\it\eta}\equiv r/r_{m}(z)$
allows us to map the conical geometry of the jet, for which
${\it\eta}\equiv r/r_{m}(z)$
allows us to map the conical geometry of the jet, for which
![]() $r_{m}=2{\it\alpha}z$
, onto a cylindrical geometry. Moreover, the use of the dimensionless concentration
$r_{m}=2{\it\alpha}z$
, onto a cylindrical geometry. Moreover, the use of the dimensionless concentration
![]() $\mathscr{C}$
ensures that in the steady state the amplitude of the scalar perturbation
$\mathscr{C}$
ensures that in the steady state the amplitude of the scalar perturbation
![]() $L_{1}=0$
, in spite of the fact that
$L_{1}=0$
, in spite of the fact that
![]() $c_{m}\sim 1/z$
, and therefore allows us to focus on departures from this state. Due to the geometry of the jet, it is unlikely that the ordinary differential equation satisfied by the perturbation
$c_{m}\sim 1/z$
, and therefore allows us to focus on departures from this state. Due to the geometry of the jet, it is unlikely that the ordinary differential equation satisfied by the perturbation
![]() $g_{1}({\it\eta})$
is the same as that which is implied by (5.4) for pipes. However, since we are primarily interested in the integral quantity
$g_{1}({\it\eta})$
is the same as that which is implied by (5.4) for pipes. However, since we are primarily interested in the integral quantity
![]() ${\it\theta}_{1}\equiv \langle f_{0}g_{1}\rangle$
, rather than the particular form of
${\it\theta}_{1}\equiv \langle f_{0}g_{1}\rangle$
, rather than the particular form of
![]() $g_{1}({\it\eta})$
, we will not attempt to obtain an exact equation for
$g_{1}({\it\eta})$
, we will not attempt to obtain an exact equation for
![]() $g_{1}({\it\eta})$
in this work.
$g_{1}({\it\eta})$
in this work.
In the absence of a well-defined edge, we define the cross-sectional average
![]() $\langle {\it\chi}\rangle$
of a quantity
$\langle {\it\chi}\rangle$
of a quantity
![]() ${\it\chi}$
in the jet according to
${\it\chi}$
in the jet according to
such that
![]() $w_{m}=\langle \overline{w}\rangle$
. For axisymmetric jets, a constant eddy viscosity
$w_{m}=\langle \overline{w}\rangle$
. For axisymmetric jets, a constant eddy viscosity
![]() ${\it\nu}_{T}$
can be expressed in terms of the entrainment coefficient according to
${\it\nu}_{T}$
can be expressed in terms of the entrainment coefficient according to
![]() ${\it\nu}_{T}={\it\alpha}w_{m}r_{m}/3$
(see Craske & van Reeuwijk Reference Craske and van Reeuwijk2015a
). Assuming that the turbulent Schmidt number
${\it\nu}_{T}={\it\alpha}w_{m}r_{m}/3$
(see Craske & van Reeuwijk Reference Craske and van Reeuwijk2015a
). Assuming that the turbulent Schmidt number
![]() ${\it\nu}_{T}/{\it\kappa}_{T}$
is approximately unity, we therefore set
${\it\nu}_{T}/{\it\kappa}_{T}$
is approximately unity, we therefore set
![]() ${\it\kappa}_{T}={\it\alpha}w_{m}r_{m}/3$
. Furthermore, the dimensionless mean scalar concentration
${\it\kappa}_{T}={\it\alpha}w_{m}r_{m}/3$
. Furthermore, the dimensionless mean scalar concentration
![]() $\mathscr{C}_{m}$
can be defined in terms of integral quantities, such that
$\mathscr{C}_{m}$
can be defined in terms of integral quantities, such that
![]() $\mathscr{C}_{m}\equiv C_{m}/C_{m0}$
, where
$\mathscr{C}_{m}\equiv C_{m}/C_{m0}$
, where
![]() $C_{m0}$
is an integral steady-state concentration. Consequently, substitution of
$C_{m0}$
is an integral steady-state concentration. Consequently, substitution of
![]() ${\it\kappa}_{T}$
,
${\it\kappa}_{T}$
,
![]() $\mathscr{C}_{m}$
and the linear dependence of the jet width on
$\mathscr{C}_{m}$
and the linear dependence of the jet width on
![]() $z$
,
$z$
,
![]() $r_{m}=2{\it\alpha}z$
, into (5.5) results in
$r_{m}=2{\it\alpha}z$
, into (5.5) results in
In the steady state, for which
![]() $C_{m}\sim z$
, it is clear from (5.7) that
$C_{m}\sim z$
, it is clear from (5.7) that
![]() $L_{1}=0$
. Using (5.2), the dispersion closure for the dimensionless scalar flux in an unsteady jet can be expressed as
$L_{1}=0$
. Using (5.2), the dispersion closure for the dimensionless scalar flux in an unsteady jet can be expressed as
As noted previously, instead of calculating
![]() $g_{0}$
and
$g_{0}$
and
![]() $g_{1}$
exactly, we treat
$g_{1}$
exactly, we treat
![]() ${\it\theta}_{0}$
and
${\it\theta}_{0}$
and
![]() ${\it\theta}_{1}$
as model parameters whose value can be determined from observation. Notable, however, is the fact that
${\it\theta}_{1}$
as model parameters whose value can be determined from observation. Notable, however, is the fact that
![]() ${\it\theta}_{0}$
can be determined from the steady-state data.
${\it\theta}_{0}$
can be determined from the steady-state data.
6. Model prediction
Substitution of (5.8) into (2.7) results in an advection–dispersion equation given by
Hereafter we will assume that
![]() $z$
and
$z$
and
![]() $t$
are coordinates relative to the location of a virtual source
$t$
are coordinates relative to the location of a virtual source
![]() $(z_{v},t_{v})$
. It is noteworthy that the advection parameter
$(z_{v},t_{v})$
. It is noteworthy that the advection parameter
![]() ${\it\theta}_{0}+6{\it\theta}_{1}$
(cf.
${\it\theta}_{0}+6{\it\theta}_{1}$
(cf.
![]() $K_{a}$
in Landel et al.
Reference Landel, Caulfield and Woods2012) contains a contribution from both
$K_{a}$
in Landel et al.
Reference Landel, Caulfield and Woods2012) contains a contribution from both
![]() ${\it\theta}_{0}$
and
${\it\theta}_{0}$
and
![]() ${\it\theta}_{1}$
, which are parameters that each have a particular physical significance and are precisely defined integrals. In particular,
${\it\theta}_{1}$
, which are parameters that each have a particular physical significance and are precisely defined integrals. In particular,
![]() ${\it\theta}_{0}$
depends on steady-state properties of the flow and can therefore be estimated a priori. Although
${\it\theta}_{0}$
depends on steady-state properties of the flow and can therefore be estimated a priori. Although
![]() ${\it\theta}_{m}={\it\theta}_{0}$
in the steady state, recognising that the longitudinal turbulent scalar flux
${\it\theta}_{m}={\it\theta}_{0}$
in the steady state, recognising that the longitudinal turbulent scalar flux
![]() ${\it\theta}_{f}$
will affect the relevant advection velocity, we equate
${\it\theta}_{f}$
will affect the relevant advection velocity, we equate
![]() ${\it\theta}_{0}$
with the observed steady-state value of
${\it\theta}_{0}$
with the observed steady-state value of
![]() ${\it\theta}_{m}+{\it\theta}_{f}\approx 1.0$
. To estimate the value of the parameter
${\it\theta}_{m}+{\it\theta}_{f}\approx 1.0$
. To estimate the value of the parameter
![]() ${\it\theta}_{1}$
, we compare the coefficient of the mixing term on the right-hand side of (6.1) with the mixing coefficient
${\it\theta}_{1}$
, we compare the coefficient of the mixing term on the right-hand side of (6.1) with the mixing coefficient
![]() $D_{e}$
that was observed in § 4. Specifically, we set
$D_{e}$
that was observed in § 4. Specifically, we set
![]() ${\it\theta}_{1}={\it\alpha}D_{e}/(3M_{m}^{1/2})=0.017$
. The prediction of
${\it\theta}_{1}={\it\alpha}D_{e}/(3M_{m}^{1/2})=0.017$
. The prediction of
![]() ${\it\theta}_{m}$
that we obtain using (5.8) with
${\it\theta}_{m}$
that we obtain using (5.8) with
![]() $({\it\theta}_{0},{\it\theta}_{1})=(1.0,0.017)$
and the observed behaviour of
$({\it\theta}_{0},{\it\theta}_{1})=(1.0,0.017)$
and the observed behaviour of
![]() $C_{m}$
is shown in figure 8. Although the model appears to overpredict the magnitude of
$C_{m}$
is shown in figure 8. Although the model appears to overpredict the magnitude of
![]() ${\it\theta}_{m}$
, it shows a good agreement with the variation of
${\it\theta}_{m}$
, it shows a good agreement with the variation of
![]() ${\it\theta}_{m}$
with respect to
${\it\theta}_{m}$
with respect to
![]() $z/z^{\ast }$
. In fact, the model shows a better agreement with the magnitude of
$z/z^{\ast }$
. In fact, the model shows a better agreement with the magnitude of
![]() ${\it\theta}_{f}+{\it\theta}_{m}$
than
${\it\theta}_{f}+{\it\theta}_{m}$
than
![]() ${\it\theta}_{m}$
, which is a consequence of the estimation of
${\it\theta}_{m}$
, which is a consequence of the estimation of
![]() ${\it\theta}_{1}$
being based on
${\it\theta}_{1}$
being based on
![]() $D_{e}$
, which is influenced by
$D_{e}$
, which is influenced by
![]() ${\it\theta}_{m}$
and
${\it\theta}_{m}$
and
![]() ${\it\theta}_{f}$
.
${\it\theta}_{f}$
.
Having established that the dispersion of a scalar in a jet is a self-similar process in § 4, we seek a similarity solution to (6.1). We express (6.1) as
with
![]() $C_{m}$
subject to the conditions
$C_{m}$
subject to the conditions
where
![]() $F_{0}$
is the source flux and
$F_{0}$
is the source flux and
![]() ${\it\lambda}^{\ast }\equiv {\it\theta}_{0}+6{\it\theta}_{1}$
is a constant that characterises the propagation speed of the front. Based on the observations reported above,
${\it\lambda}^{\ast }\equiv {\it\theta}_{0}+6{\it\theta}_{1}$
is a constant that characterises the propagation speed of the front. Based on the observations reported above,
![]() ${\it\lambda}^{\ast }\approx 1.10$
. Introducing the similarity variable
${\it\lambda}^{\ast }\approx 1.10$
. Introducing the similarity variable
we propose a solution for
![]() $C_{m}$
of the form
$C_{m}$
of the form
Transformation of (6.2) according to (6.5) and (6.4) results in
where
![]() $\mathit{Pe}\equiv {\it\lambda}^{\ast }M_{m}^{1/2}/(2{\it\alpha}D_{e})\approx 10.99$
, based on our observations. The transformed boundary condition and integral constraint become
$\mathit{Pe}\equiv {\it\lambda}^{\ast }M_{m}^{1/2}/(2{\it\alpha}D_{e})\approx 10.99$
, based on our observations. The transformed boundary condition and integral constraint become
Equation (6.6) has the general solution
where
![]() $\text{G}$
is the hypergeometric function. Exact expressions for the constants
$\text{G}$
is the hypergeometric function. Exact expressions for the constants
![]() $c_{1}$
and
$c_{1}$
and
![]() $c_{2}$
, in terms of the parameters
$c_{2}$
, in terms of the parameters
![]() $\mathit{Pe}$
and
$\mathit{Pe}$
and
![]() ${\it\lambda}^{\ast }$
, are provided in appendix C. Using
${\it\lambda}^{\ast }$
, are provided in appendix C. Using
![]() $\mathit{Pe}\approx 10.99$
and
$\mathit{Pe}\approx 10.99$
and
![]() ${\it\lambda}^{\ast }\approx 1.10$
, we find
${\it\lambda}^{\ast }\approx 1.10$
, we find
![]() $c_{1}=-25.79$
and
$c_{1}=-25.79$
and
![]() $c_{2}=1.00$
.
$c_{2}=1.00$
.
Figure 9 demonstrates that the similarity solution (6.8) agrees reasonably well with the observed data. In particular, the model reproduces the shape and the longitudinal extent of the scalar’s distribution. The model solution appears to slightly overpredict the peak concentration, and the concentration in the tail of the distribution at relatively large values of
![]() ${\it\lambda}$
. We attribute the latter to higher-order contributions in the dimensionless scalar flux
${\it\lambda}$
. We attribute the latter to higher-order contributions in the dimensionless scalar flux
![]() ${\it\theta}_{m}$
, for which (5.2) does not account (cf. the higher-order terms for dispersion in a pipe flow considered by Chatwin Reference Chatwin1970). However, given that the model is based on a leading-order representation of the front involving two parameters, and that the specification of
${\it\theta}_{m}$
, for which (5.2) does not account (cf. the higher-order terms for dispersion in a pipe flow considered by Chatwin Reference Chatwin1970). However, given that the model is based on a leading-order representation of the front involving two parameters, and that the specification of
![]() ${\it\theta}_{0}$
was made a priori, the agreement is satisfactory.
${\it\theta}_{0}$
was made a priori, the agreement is satisfactory.
7. Planar jets
Although the dispersion model described in this paper has been developed for axisymmetric jets, it is built from general principles that are equally applicable in the analysis of planar jets or plumes. Central to the model are the geometric parameters
![]() ${\it\theta}_{0}=\langle f_{0}g_{0}\rangle$
and
${\it\theta}_{0}=\langle f_{0}g_{0}\rangle$
and
![]() ${\it\theta}_{1}=\langle f_{0}g_{1}\rangle$
, which correspond to the dimensionless scalar flux of the steady state and of the perturbed scalar profile respectively. Both
${\it\theta}_{1}=\langle f_{0}g_{1}\rangle$
, which correspond to the dimensionless scalar flux of the steady state and of the perturbed scalar profile respectively. Both
![]() ${\it\theta}_{0}$
and
${\it\theta}_{0}$
and
![]() ${\it\theta}_{1}$
are functions of the dimensionless longitudinal velocity
${\it\theta}_{1}$
are functions of the dimensionless longitudinal velocity
![]() $f_{0}({\it\eta})$
, the scalar concentration
$f_{0}({\it\eta})$
, the scalar concentration
![]() $g_{0}({\it\eta})$
and the perturbed concentration
$g_{0}({\it\eta})$
and the perturbed concentration
![]() $g_{1}({\it\eta})$
. Due to the fact that
$g_{1}({\it\eta})$
. Due to the fact that
![]() $g_{1}({\it\eta})$
can be determined a priori by solving an ordinary differential equation involving
$g_{1}({\it\eta})$
can be determined a priori by solving an ordinary differential equation involving
![]() $g_{0}$
, the dimensionless perturbation flux
$g_{0}$
, the dimensionless perturbation flux
![]() ${\it\theta}_{1}$
can, in principle, be determined without consulting unsteady data.
${\it\theta}_{1}$
can, in principle, be determined without consulting unsteady data.
In contrast, Landel et al. (Reference Landel, Caulfield and Woods2012), while providing several analytical solutions and insights from experiments, relied on advection and dispersion parameters (
![]() $K_{a}$
and
$K_{a}$
and
![]() $K_{d}$
respectively), whose relationship with the underlying turbulent scalar flux
$K_{d}$
respectively), whose relationship with the underlying turbulent scalar flux
![]() $\overline{w^{\prime }c^{\prime }}$
or mean flow scalar flux
$\overline{w^{\prime }c^{\prime }}$
or mean flow scalar flux
![]() $\overline{w}\,\overline{c}$
was not made explicit. However, the validity of both the model presented by Landel et al. (Reference Landel, Caulfield and Woods2012) for dispersion in quasi-two-dimensional jets (1.2), and the framework we propose is strengthened by the fact that when our dispersion closure is applied to planar jets we find (see appendix B)
$\overline{w}\,\overline{c}$
was not made explicit. However, the validity of both the model presented by Landel et al. (Reference Landel, Caulfield and Woods2012) for dispersion in quasi-two-dimensional jets (1.2), and the framework we propose is strengthened by the fact that when our dispersion closure is applied to planar jets we find (see appendix B)
which is in one-to-one correspondence with (1.2) when
It is important to note, however, the fundamental physical difference between a statistically two-dimensional turbulent planar jet and the quasi-two-dimensional jet studied by Landel et al. (Reference Landel, Caulfield and Woods2012) by confining the jet to the narrow gap between two parallel plates. Although our treatment in appendix B applies equally well to each of these cases, one would expect dimensionless parameters such as the entrainment coefficient
![]() ${\it\alpha}$
and
${\it\alpha}$
and
![]() ${\it\theta}_{1}$
to depend on the particular case considered.
${\it\theta}_{1}$
to depend on the particular case considered.
Not straightforward to anticipate from (1.2) is that the advection parameter
![]() $K_{a}$
depends on both
$K_{a}$
depends on both
![]() ${\it\theta}_{0}$
and
${\it\theta}_{0}$
and
![]() ${\it\theta}_{1}$
. Using (7.2), it is useful to compute the values of
${\it\theta}_{1}$
. Using (7.2), it is useful to compute the values of
![]() ${\it\theta}_{0}$
and
${\it\theta}_{0}$
and
![]() ${\it\theta}_{1}$
that correspond to
${\it\theta}_{1}$
that correspond to
![]() $K_{a}=1.65$
and
$K_{a}=1.65$
and
![]() $K_{d}=0.09$
, as reported by Landel et al. (Reference Landel, Caulfield and Woods2012):
$K_{d}=0.09$
, as reported by Landel et al. (Reference Landel, Caulfield and Woods2012):
In planar jets, the dispersion closure used in (7.1) has the form (see appendix B)
While it may appear inconvenient that (7.5) contains prefactors that differ from those in the equivalent expression for axisymmetric jets (5.8), the advantage is that the physical meaning of
![]() ${\it\theta}_{0}$
and
${\it\theta}_{0}$
and
![]() ${\it\theta}_{1}$
is unchanged. In principle, one is therefore able to make predictions a priori about dispersion in planar/quasi-two-dimensional jets in addition to axisymmetric jets.
${\it\theta}_{1}$
is unchanged. In principle, one is therefore able to make predictions a priori about dispersion in planar/quasi-two-dimensional jets in addition to axisymmetric jets.
8. Conclusions
We have analysed the transport of a passive scalar in a statistically axisymmetric turbulent jet and found that the longitudinal mixing is primarily the result of shear-flow dispersion rather than turbulent transport (see, e.g. figure 8). Consequently, estimations of the amount of longitudinal mixing based exclusively on turbulence that do not account for the radial dependence of the mean flow are likely to significantly underestimate the total longitudinal mixing.
While shear-flow dispersion in turbulent jets is ostensibly different from shear-flow dispersion in pipe flows, for which the classical theory was first developed (Taylor Reference Taylor1953), there are several similarities. Different from pipe flow is the fact that in a jet the radial steady-state scalar concentration is non-uniform, and will, according to the lateral transport properties of the scalar, be concentrated in regions of relatively high longitudinal velocity. From an integral perspective, this property of the scalar field is characterised by a constant dimensionless flux parameter
![]() ${\it\theta}_{0}$
. Similar to pipe flow is the fact that longitudinal changes in an otherwise steady-state scalar field result in a local perturbation of the scalar’s radial dependence. In jets, the effect of a perturbation of amplitude
${\it\theta}_{0}$
. Similar to pipe flow is the fact that longitudinal changes in an otherwise steady-state scalar field result in a local perturbation of the scalar’s radial dependence. In jets, the effect of a perturbation of amplitude
![]() $L_{1}$
on the local scalar flux can be accounted for with the parameter
$L_{1}$
on the local scalar flux can be accounted for with the parameter
![]() ${\it\theta}_{1}$
. Together,
${\it\theta}_{1}$
. Together,
![]() ${\it\theta}_{0}$
and
${\it\theta}_{0}$
and
![]() $L_{1}{\it\theta}_{1}$
provide a dispersion closure in an integral model that shows good agreement with DNS data (figure 9). When applied to planar jets the approach yields a differential equation that is in one-to-one correspondence with that proposed by Landel et al. (Reference Landel, Caulfield and Woods2012) and provides additional physical insight.
$L_{1}{\it\theta}_{1}$
provide a dispersion closure in an integral model that shows good agreement with DNS data (figure 9). When applied to planar jets the approach yields a differential equation that is in one-to-one correspondence with that proposed by Landel et al. (Reference Landel, Caulfield and Woods2012) and provides additional physical insight.
In principle, shear-flow dispersion finds application in any problem in which there are lateral gradients in a velocity field, and is therefore relevant to a wide range of situations in industrial and environmental fluid mechanics. In particular, one should expect to find shear-flow dispersion in both laminar and turbulent free-shear flows, including turbulent plumes and wakes. The axisymmetric turbulent jet that we have analysed is relatively simple because it is statistically two-dimensional and self-similar at relatively large distances from the source. Consequently, the behaviour of a propagating step change in the integral concentration could be characterised completely in terms of a similarity variable
![]() ${\it\lambda}\propto z^{2}/t$
. However, one expects shear-flow dispersion to also play a role in more complicated three-dimensional problems such as plumes that are influenced by a cross-wind and multiple coalescing jets and plumes. The present study indicates that unless shear-flow dispersion, arising from advection by the mean flow, is correctly understood and parameterised, longitudinal mixing in such flows will not be predicted correctly.
${\it\lambda}\propto z^{2}/t$
. However, one expects shear-flow dispersion to also play a role in more complicated three-dimensional problems such as plumes that are influenced by a cross-wind and multiple coalescing jets and plumes. The present study indicates that unless shear-flow dispersion, arising from advection by the mean flow, is correctly understood and parameterised, longitudinal mixing in such flows will not be predicted correctly.
Outstanding among issues deserving further attention is a formulation for the precise way in which the scalar profile is perturbed as a result of a step change in the longitudinal concentration profile. Such a formulation would allow one to estimate a dispersion coefficient (cf.
![]() ${\it\theta}_{1}$
in the present study) for a variety of different free-shear flows such as planar jets and plumes. A related issue for consideration is the role of higher-order perturbations to the scalar profile such as those considered in the context of pipe flow by Taylor (Reference Taylor1954a
), Gill (Reference Gill1967) and Chatwin (Reference Chatwin1970).
${\it\theta}_{1}$
in the present study) for a variety of different free-shear flows such as planar jets and plumes. A related issue for consideration is the role of higher-order perturbations to the scalar profile such as those considered in the context of pipe flow by Taylor (Reference Taylor1954a
), Gill (Reference Gill1967) and Chatwin (Reference Chatwin1970).
Acknowledgements
The authors are grateful for the computational resources provided by the High Performance Computing Facility at Imperial College and the UK Turbulence Consortium under grant number EP/L000261/1. J.C. gratefully acknowledges funding from the Engineering and Physical Sciences Research Council (EPSRC) under grant number EP/J500239/1. Supporting data for this article are available on request: please contact either m.vanreeuwijk@imperial.ac.uk or civilsfluids@imperial.ac.uk.
Appendix A. Shear-flow dispersion in a pipe
Following Taylor (Reference Taylor1953, Reference Taylor1954b
), we consider the evolution of a step change in the dimensionless concentration
![]() $\mathscr{C}\equiv \overline{c}/c_{m0}$
in a pipe or tube of radius
$\mathscr{C}\equiv \overline{c}/c_{m0}$
in a pipe or tube of radius
![]() $r_{m}$
. Consistent with boundary layer theory we neglect second derivatives in the longitudinal direction. Unlike jets, in pipes the steady-state concentration
$r_{m}$
. Consistent with boundary layer theory we neglect second derivatives in the longitudinal direction. Unlike jets, in pipes the steady-state concentration
![]() $c_{m0}$
is independent of
$c_{m0}$
is independent of
![]() $z$
, and we can replace
$z$
, and we can replace
![]() $\overline{c}$
with
$\overline{c}$
with
![]() $\mathscr{C}$
in the scalar transport equation:
$\mathscr{C}$
in the scalar transport equation:
where
![]() ${\it\kappa}_{T}$
is the (constant) eddy diffusivity and
${\it\kappa}_{T}$
is the (constant) eddy diffusivity and
![]() $\overline{w}$
is the steady-state velocity field. Taylor (Reference Taylor1953) applied a Galilean transform, defining a coordinate system that moves according to the mean longitudinal velocity or, equivalently, the velocity associated with the scalar flux:
$\overline{w}$
is the steady-state velocity field. Taylor (Reference Taylor1953) applied a Galilean transform, defining a coordinate system that moves according to the mean longitudinal velocity or, equivalently, the velocity associated with the scalar flux:
where
![]() ${\it\theta}_{0}$
is constant and equal to unity for pipe flow. We assume that the radial dependence of the velocity field does not vary in the longitudinal direction, such that
${\it\theta}_{0}$
is constant and equal to unity for pipe flow. We assume that the radial dependence of the velocity field does not vary in the longitudinal direction, such that
![]() $\overline{w}=w_{m}f_{0}({\it\eta})$
, where
$\overline{w}=w_{m}f_{0}({\it\eta})$
, where
![]() $w_{m}=\langle \overline{w}\rangle$
is the cross-sectional-averaged longitudinal velocity,
$w_{m}=\langle \overline{w}\rangle$
is the cross-sectional-averaged longitudinal velocity,
![]() ${\it\eta}\equiv r/r_{m}$
is a normalised radius and
${\it\eta}\equiv r/r_{m}$
is a normalised radius and
![]() $\langle f_{0}\rangle =1$
. Equation (A 1) transforms according to
$\langle f_{0}\rangle =1$
. Equation (A 1) transforms according to
The radial dependence of
![]() $\mathscr{C}$
can be decomposed into
$\mathscr{C}$
can be decomposed into
![]() $g_{0}({\it\eta})$
, which corresponds to the steady-state radial dependence of the concentration, and
$g_{0}({\it\eta})$
, which corresponds to the steady-state radial dependence of the concentration, and
![]() $g_{1}({\it\eta})$
, which accounts for the leading-order perturbation from
$g_{1}({\it\eta})$
, which accounts for the leading-order perturbation from
![]() $g_{0}({\it\eta})$
:
$g_{0}({\it\eta})$
:
Here, the variable
![]() $\mathscr{C}_{m}$
determines the amplitude of the concentration profile. For pipe flow, since the steady-state concentration is uniform, it can be assumed that
$\mathscr{C}_{m}$
determines the amplitude of the concentration profile. For pipe flow, since the steady-state concentration is uniform, it can be assumed that
![]() $g_{0}=1$
, without loss of generality, and we define
$g_{0}=1$
, without loss of generality, and we define
![]() $\mathscr{C}_{m}$
such that the cross-sectional average
$\mathscr{C}_{m}$
such that the cross-sectional average
![]() $\langle g_{1}\rangle =0$
. In (A 4),
$\langle g_{1}\rangle =0$
. In (A 4),
![]() $L_{1}$
determines the amplitude of the leading-order perturbation.
$L_{1}$
determines the amplitude of the leading-order perturbation.
Applying the averaging operation
![]() $\langle \,\rangle$
to (A 3) gives an equation for the mean concentration:
$\langle \,\rangle$
to (A 3) gives an equation for the mean concentration:
Subtracting (A 5) from (A 3) yields
Taylor’s key assumption was that for large time (
![]() $t\gg r_{m}^{2}/{\it\kappa}_{T}$
) there exists an asymptotic balance between the second and fourth terms in (A 6). Noting that
$t\gg r_{m}^{2}/{\it\kappa}_{T}$
) there exists an asymptotic balance between the second and fourth terms in (A 6). Noting that
![]() $\partial _{{\it\xi}}=\partial _{z}$
, one therefore assumes that
$\partial _{{\it\xi}}=\partial _{z}$
, one therefore assumes that
which represents a balance between longitudinal advection and turbulent transport in the radial direction. Equation (A 7) has a separable form and implies that to within a constant multiplicative factor
In principle, (A 7) can be inverted to determine the form of the perturbation
![]() $g_{1}$
, and therefore the flux
$g_{1}$
, and therefore the flux
Defining
(A 9) can be expressed as
![]() ${\it\theta}_{m}={\it\theta}_{0}+L_{1}{\it\theta}_{1}$
. The parameter
${\it\theta}_{m}={\it\theta}_{0}+L_{1}{\it\theta}_{1}$
. The parameter
![]() ${\it\theta}_{0}$
is the basic steady-state dimensionless scalar flux arising from self-similar profiles of
${\it\theta}_{0}$
is the basic steady-state dimensionless scalar flux arising from self-similar profiles of
![]() $\overline{c}$
, and
$\overline{c}$
, and
![]() ${\it\theta}_{1}$
is the dimensionless scalar flux arising from a local departure from self-similarity in
${\it\theta}_{1}$
is the dimensionless scalar flux arising from a local departure from self-similarity in
![]() $\overline{c}$
.
$\overline{c}$
.
Appendix B. Shear-flow dispersion in a planar jet
The approach taken in § 5 to obtain a model for shear-flow dispersion in axisymmetric jets is equally applicable to planar jets. Since planar jets are driven by line sources of momentum flux of infinite length, we will assume that the scalar is also released over a line source of infinite length coincident with the source of momentum flux. For planar jets we define the volume flux, momentum flux and integral scalar concentration, per unit length, according to
respectively. Consequently, it is convenient to define top-hat variables
![]() $r_{m}$
and
$r_{m}$
and
![]() $w_{m}$
such that
$w_{m}$
such that
![]() $Q_{m}\equiv 2w_{m}r_{m}$
and
$Q_{m}\equiv 2w_{m}r_{m}$
and
![]() $M_{m}\equiv 2w_{m}^{2}r_{m}$
; hence
$M_{m}\equiv 2w_{m}^{2}r_{m}$
; hence
![]() $w_{m}\equiv M_{m}/Q_{m}$
and
$w_{m}\equiv M_{m}/Q_{m}$
and
![]() $r_{m}\equiv Q_{m}^{2}/(2M_{m})$
. For two-dimensional jets the averaging operator
$r_{m}\equiv Q_{m}^{2}/(2M_{m})$
. For two-dimensional jets the averaging operator
![]() $\langle \,\rangle$
therefore becomes
$\langle \,\rangle$
therefore becomes
which ensures that
![]() $w_{m}=\langle \overline{w}\rangle$
. Consistent with the definitions above, in the limit
$w_{m}=\langle \overline{w}\rangle$
. Consistent with the definitions above, in the limit
![]() $r_{d}\rightarrow \infty$
, is a Gaussian velocity profile of the form
$r_{d}\rightarrow \infty$
, is a Gaussian velocity profile of the form
where
![]() ${\it\eta}\equiv r/r_{m}$
. The two-dimensional steady jet equations are
${\it\eta}\equiv r/r_{m}$
. The two-dimensional steady jet equations are
representing volume conservation and momentum conservation respectively. It should be noted that the
![]() ${\it\alpha}$
defined by (B 4a,b
) is a factor of
${\it\alpha}$
defined by (B 4a,b
) is a factor of
![]() $\sqrt{2}$
larger than the value of
$\sqrt{2}$
larger than the value of
![]() ${\it\alpha}$
used by Landel et al. (Reference Landel, Caulfield and Woods2012), who scale the entrainment velocity on the maximum velocity, which is equal to
${\it\alpha}$
used by Landel et al. (Reference Landel, Caulfield and Woods2012), who scale the entrainment velocity on the maximum velocity, which is equal to
![]() $\sqrt{2}w_{m}$
. The solution to this system of equations is
$\sqrt{2}w_{m}$
. The solution to this system of equations is
![]() $Q_{m}=2\sqrt{{\it\alpha}zM_{0}}$
, where
$Q_{m}=2\sqrt{{\it\alpha}zM_{0}}$
, where
![]() $M_{m}=M_{0}$
is the momentum flux per unit length at the source. In a steady planar jet there is a balance between the longitudinal transport of mean kinetic energy and the production of turbulence (for an axisymmetric jet see Craske & van Reeuwijk Reference Craske and van Reeuwijk2015a
, for details):
$M_{m}=M_{0}$
is the momentum flux per unit length at the source. In a steady planar jet there is a balance between the longitudinal transport of mean kinetic energy and the production of turbulence (for an axisymmetric jet see Craske & van Reeuwijk Reference Craske and van Reeuwijk2015a
, for details):
where
![]() ${\it\gamma}_{m}$
and
${\it\gamma}_{m}$
and
![]() ${\it\delta}_{m}$
are the dimensionless energy flux and dimensionless turbulence production respectively, defined as
${\it\delta}_{m}$
are the dimensionless energy flux and dimensionless turbulence production respectively, defined as
Using (B 3), the dimensionless energy flux
![]() ${\it\gamma}_{m}$
can be expressed as
${\it\gamma}_{m}$
can be expressed as
Moreover, invoking a gradient-diffusion hypothesis,
the dimensionless turbulence production can be expressed as
When (B 5) is combined with (B 4a,b
) we find that the relationship between
![]() ${\it\delta}_{m},{\it\gamma}_{m}$
and
${\it\delta}_{m},{\it\gamma}_{m}$
and
![]() ${\it\alpha}$
is
${\it\alpha}$
is
![]() ${\it\alpha}=-{\it\delta}_{m}/2{\it\gamma}_{m}$
; hence
${\it\alpha}=-{\it\delta}_{m}/2{\it\gamma}_{m}$
; hence
In two dimensions, setting
![]() ${\it\kappa}_{T}={\it\nu}_{T}$
, equation (A 8) therefore becomes
${\it\kappa}_{T}={\it\nu}_{T}$
, equation (A 8) therefore becomes
The steady-state integral concentration
![]() $C_{m0}$
in a planar jet scales according to
$C_{m0}$
in a planar jet scales according to
![]() $\sqrt{z}$
. Therefore, noting that for a planar jet
$\sqrt{z}$
. Therefore, noting that for a planar jet
![]() $r_{m}=2{\it\alpha}z$
, substituting
$r_{m}=2{\it\alpha}z$
, substituting
![]() $\mathscr{C}_{m}\equiv C_{m}/C_{m0}\sim C_{m}/\sqrt{z}$
in (B 11), we find
$\mathscr{C}_{m}\equiv C_{m}/C_{m0}\sim C_{m}/\sqrt{z}$
in (B 11), we find
Substitution of (B 12) and
![]() ${\it\theta}_{m}={\it\theta}_{0}+L_{1}{\it\theta}_{1}$
into the transport equation for a scalar in a planar jet,
${\it\theta}_{m}={\it\theta}_{0}+L_{1}{\it\theta}_{1}$
into the transport equation for a scalar in a planar jet,
gives
which is the planar version of the axisymmetric dispersion model (6.1), and has a form that is identical to that which was proposed by Landel et al. (Reference Landel, Caulfield and Woods2012) for quasi-two-dimensional jets.
Appendix C. Similarity solution constants
For large
![]() ${\it\lambda}$
equation (6.8) can be expressed as
${\it\lambda}$
equation (6.8) can be expressed as
hence
 $$\begin{eqnarray}c_{2}=\underbrace{-\!\left(\frac{\mathit{Pe}}{2{\it\lambda}^{\ast }}\right)^{1/2-\mathit{Pe}/2}{\it\Gamma}\left(\frac{1}{2}+\frac{\mathit{Pe}}{2}\right)}_{c_{3}}c_{1},\end{eqnarray}$$
$$\begin{eqnarray}c_{2}=\underbrace{-\!\left(\frac{\mathit{Pe}}{2{\it\lambda}^{\ast }}\right)^{1/2-\mathit{Pe}/2}{\it\Gamma}\left(\frac{1}{2}+\frac{\mathit{Pe}}{2}\right)}_{c_{3}}c_{1},\end{eqnarray}$$
to ensure that
![]() ${\it\Phi}\rightarrow 0$
as
${\it\Phi}\rightarrow 0$
as
![]() ${\it\lambda}\rightarrow \infty$
. The value of the remaining degree of freedom
${\it\lambda}\rightarrow \infty$
. The value of the remaining degree of freedom
![]() $c_{1}$
is determined by the integral constraint (6.7b
):
$c_{1}$
is determined by the integral constraint (6.7b
):
Using the observed values
![]() $\mathit{Pe}\approx 10.99$
and
$\mathit{Pe}\approx 10.99$
and
![]() ${\it\lambda}^{\ast }\approx 1.10$
, we find
${\it\lambda}^{\ast }\approx 1.10$
, we find
![]() $c_{1}=-25.79$
and
$c_{1}=-25.79$
and
![]() $c_{2}=1.00$
.
$c_{2}=1.00$
.