Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-25T15:05:38.336Z Has data issue: false hasContentIssue false
  • English
  • Français

Sensitivity of high-speed boundary-layer stability to base-flow distortion

Published online by Cambridge University Press:  21 November 2018

J. Park Open the ORCID record for J. Park [Opens in a new window]  and
T. A. Zaki Open the ORCID record for T. A. Zaki [Opens in a new window]
J. Park
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
T. A. Zaki*
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
*
†Email address for correspondence: t.zaki@jhu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The linear stability of high-speed boundary layers can be altered by distortions to the base velocity and temperature profiles. An analytic expression for the sensitivity is derived for parallel and spatially developing boundary layers, the latter using linear parabolized stability equations and their adjoint. Both the slow mode, S, and the fast mode, F, are investigated at Mach number 4.5. The mode S is more sensitive with respect to distortion in base velocity than in base temperature. The sensitivity is largest within the boundary layer away from the wall. Near the critical layer, where the phase speed of the mode equals the base streamwise velocity, the sensitivity to the base streamwise velocity is negative. For the mode F, there is a discontinuous jump in the sensitivity when the phase speed is below unity, and a critical layer is established. The sensitivity of the two modes increases with the Reynolds number, but there is a sudden drop and a jump in the sensitivities of the modes S and F, respectively, near the synchronization point where the phase speeds of the two modes are equal. Furthermore, the maximum uncertainty bounds are obtained for the distorted base state that maximizes the destabilization or stabilization of the modes by solving the Lagrangian optimization problem for the sensitivity. The sensitivity of the flow stability to surface heating is then studied, and changes in growth rate and the 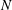$N$-factor are evaluated. The formulation provides a clear physical interpretation of these changes, and establishes uncertainty bounds for stability predictions for a given level of uncertainty in wall temperature.

JFM classification

Boundary Layers: Boundary Layers Boundary Layers: Boundary layer stability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 859 , 25 January 2019 , pp. 476 - 515
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amoignon, O. G., Pralits, J. O., Hanifi, A., Berggren, M. & Henningson, D. S. 2006 Shape optimization for delay of laminar-turbulent transition. AIAA J. 44, 1009–1024.Google Scholar
Antkoiwak, A. & Brancher, P. 2004 Transient energy growth for the Lamb–Oseen vortex. Phys. Fluids 16, L1–L4.Google Scholar
Balakumar, P.2009 Stability of supersonic boundary layers on a cone at an angle of attack. In AIAA 39th Fluid Dynamics Conference and Exhibit. AIAA-2009-3555.Google Scholar
Balakumar, P. & King, R. A.2010 Receptivity and transition of supersonic boundary layers over swept wings. In AIAA 48th Aerospace Sciences Meeting. AIAA-2010-1454.Google Scholar
Balakumar, P. & Malik, M. R. 1992 Discrete modes and continuous spectra in supersonic boundary layers. J. Fluid Mech. 239, 631–656.Google Scholar
Balakumar, P. & Owens, L. R.2010 Stability of hypersonic boundary layers on a cone at an angle of attack. In 40th Fluid Dynamics Conference. AIAA-2010-4718.Google Scholar
Bertolotti, F. P.1991 Linear and nonlinear stability of boundary layers with streamwise varying properties. PhD thesis, The Ohio State University.Google Scholar
Bertolotti, F. P. & Herbert, Th. 1991 Analysis of the linear stability of compressible boundary layers using the PSE. Theor. Comput. Fluid Dyn. 3, 117–124.Google Scholar
Bottaro, A., Corbett, P. & Luchini, P. 2003 The effect of base flow variation on flow stability. J. Fluid Mech. 476, 293–302.Google Scholar
Brandt, L., Sipp, D., Pralits, J. O. & Marquet, O. 2011 Effect of base-flow variation in noise-amplifiers: the flat-plate boundary layer. J. Fluid Mech. 687, 503–528.Google Scholar
Chang, C., Malik, M., Erlebacher, G. & Hussaini, M.1993 Linear and nonlinear PSE for compressible boundary layer. Tech. Rep. 93-70. Inst. Comput. Appl. Sci. Eng., Hampton, VA.Google Scholar
Chang, C.-L. & Malik, M. R. 1994 Oblique-mode breakdown and secondary instability in supersonic boundary layers. J. Fluid Mech. 273, 323–360.Google Scholar
Chen, L., Xiao, Z., Shi, Y. & Chen, S. 2017 Constrained large-eddy simulation of supersonic turbulent boundary layer over a compression ramp. J. Turbul. 18, 781–808.Google Scholar
Cheung, L. C.2007 Aeroacoustic noise prediction and the dynamics of shear layers and jets using the nonlinear parabolized stability equations. PhD thesis, Stanford University.Google Scholar
Cheung, L. C. & Zaki, T. A. 2010 Linear and nonlinear instability waves in spatially developing two-phase mixing layers. Phys. Fluids 22, 052103.Google Scholar
Cheung, L. C. & Zaki, T. A. 2011 A nonlinear PSE method for two-fluid shear flows with complex interfacial topology. J. Comput. Phys. 230, 6756–6777.Google Scholar
Day, M. J., Mansour, N. N. & Reynolds, W. C. 2001 Nonlinear stability and structure of compressible mixing layers. J. Fluid Mech. 446, 375–408.Google Scholar
Demetriades, A. 1960 An experiment on the stability of hypersonic laminar boundary layers. J. Fluid Mech. 7, 385–396.Google Scholar
Dobrinsky, A. Y.2003 Adjoint analysis for receptivity prediction. PhD thesis, Rice University.Google Scholar
Driest, E. R. & Van McCauley, W. D. 1960 The effect of controlled three-dimensional roughness on boundary-layer transition at supersonic speed. J. Aero. Sci. 27 (4), 261–271.Google Scholar
El-Hady, N. M. 1992 Secondary instability of high-speed flows and the influence of cooling and suction. Phys. Fluids A 4, 727–743.Google Scholar
Fedorov, A. 2011 Transition and stability of high-speed boundary layers. Annu. Rev. Fluid Mech. 43, 79–95.Google Scholar
Fedorov, A. & Tumin, A. 2011 High-speed boundary-layer instability: old terminology and a new framework. AIAA J. 49 (8), 1647–1657.Google Scholar
Fedorov, A. V. & Khokhlov, A. P. 2001 Prehistory of instability in a hypersonic boundary layer. Theor. Comput. Fluid Dyn. 14, 359–375.Google Scholar
Forgoston, E. & Tumin, A. 2005 Initial-value problem for three-dimensional disturbances in a compressible boundary layer. Phys. Fluids 17, 084106.Google Scholar
Frendi, A., Maestrello, L. & Bayliss, A. 1993 Coupling between a supersonic boundary layer and a flexible surface. AIAA J. 31 (4), 708–713.Google Scholar
Fujii, K. 2006 Experiment of the two-dimensional roughness effect on hypersonic boundary-layer transition. J. Spacecr. Rockets 43, 731–738.Google Scholar
Gasperas, G.1987 The stability of the compressible boundary layer on a sharp cone at zero angle of attack. In AIAA 25th Aerospace Sciences Meeting. AIAA-87-0494.Google Scholar
Germain, P. D. & Hornung, H. G. 1997 Transition on a slender cone in hypervelocity flow. Exp. Fluids 22, 183–190.Google Scholar
Graziosi, P. & Brown, G. L. 2002 Experiments on stability and transition at Mach 3. J. Fluid Mech. 472, 83–124.Google Scholar
Grilli, M., Hickel, S. & Adams, N. A. 2013 Large-eddy simulation of a supersonic turbulent boundary layer over a compression-expansion ramp. Intl J. Heat Fluid Flow 42, 79–93.Google Scholar
Guarini, S. E., Moser, R. D., Shariff, K. & Wray, A. 2000 Direct numerical simulation of a supersonic turbulent boundary layer at Mach 2.5. J. Fluid Mech. 414, 1–33.Google Scholar
Guschin, V. R. & Fedorov, A. V. 1990 Excitation and development of unstable disturbances in supersonic boundary layer. Fluid Dyn. 25 (3), 344–352.Google Scholar
Hanifi, A., Schmid, P. J. & Henningson, D. S. 1996 Transient growth in compressible boundary layer flow. Phys. Fluids 8, 826–837.Google Scholar
Hu, S. & Zhong, X.1997 Linear stability of hypersonic flow over a parabolic leading edge. In AIAA 28th Fluid Dynamics Conference. AIAA-97-2015.Google Scholar
Iyer, P. S., Muppidi, S. & Mahesh, K.2011 Roughness-induced transition in high-speed flows. In 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. AIAA-2011-566.Google Scholar
Jewell, J. S. & Kimmel, R. L. 2017 Boundary-layer stability analysis for Stetson’s Mach 6 Blunt-cone experiments. J. Spacecr. Rockets 54, 258–265.Google Scholar
Joo, J. & Durbin, P. A. 2012 Continuous mode transition in high-speed boundary-layers. Flow Turbul. Combust. 88, 407–430.Google Scholar
Kendall, J. M. 1975 Stability of supersonic boundary layers on a cone at an angle of attack. AIAA J. 13, 290–299.Google Scholar
Kimmel, R. K. 1999 Trends in hypersonic boundary layer stability and transition research. In AIP Conference Proceedings, vol. 458, pp. 1181–1186.Google Scholar
Kimmel, R. L. & Adamczak, D. W.2017 HIFiRE-5b flight overview. In AIAA 47th Fluid Dynamics Conference. AIAA-2017-3131.Google Scholar
Kocian, T. S., Moyes, A. J., Mullen, D. & Reed, H. L.2016 PSE and spatial biglobal instability analysis of HIFiRE-5 geometry. In AIAA 46th Fluid Dynamics Conference. AIAA-2016-3346.Google Scholar
Kosinov, A. D., Maslov, A. A. & Shevelkov, S. G. 1990 Experiments on the stability of supersonic laminar boundary layers. J. Fluid Mech. 219, 621–633.Google Scholar
Laurence, S. J., Wagner, A., Hannemann, K., Tanno, H. & Itoh, K. 2012 Time-resolved visualization of instability waves in a hypersonic boundary layer. AIAA J. 50, 243–246.Google Scholar
Lees, L. & Lin, C. C.1946 Investigation of the stability of the laminar boundary layer in a compressible fluid. Tech. Rep. 1115. California Institute of Technology.Google Scholar
Lees, L. & Reshotko, E. 1962 Stability of the compressible laminar boundary layer. J. Fluid Mech. 12, 555–590.Google Scholar
Lei, J. & Zhong, X.2010 Linear Stability analysis of nose bluntness effects on hypersonic boundary layer transition. In AIAA 48th Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. AIAA-2010-898.Google Scholar
Li, X., Fu, D. & Ma, Y. 2010 Direct numerical simulation of hypersonic boundary layer transition over a blunt cone with a small angle of attack. Phys. Fluids 22, 025105.Google Scholar
Lysenko, V. I. & Maslov, A. A. 1984 The effect of cooling on supersonic boundary-layer stability. J. Fluid Mech. 147, 39–52.Google Scholar
Mack, C. J., Schmid, P. J. & Sesterhenn, J. L. 2008 Global stability of swept flow around a parabolic body: connecting attachment-line and crossflow modes. J. Fluid Mech. 611, 205–214.Google Scholar
Mack, L. M.1969 Boundary layer stability theory. Tech. Rep. JPL Rept. 900-277. Jet Propulsion Lab., California Inst. of Technology, Pasadena, CA.Google Scholar
Mack, L. M. 1975 Linear stability theory and the problem of supersonic boundary-layer transition. AIAA J. 13, 278–289.Google Scholar
Mack, L. M.1987 Stability of axisymmetric boundary layers on sharp cones at hypersonic Mach numbers. In AIAA 19th Fluid Dynamics, Plasma Dynamics and Lasers Conference. AIAA-87-1413.Google Scholar
Malik, M. R. 1990 Numerical methods for hypersonic boundary layer stability. J. Comput. Phys. 86, 376–413.Google Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.Google Scholar
Martin, P. 2007 Direct numerical simulation of hypersonic turbulent boundary layers. Part 1. Initialization and comparison with experiments. J. Fluid Mech. 570, 347–364.Google Scholar
Masad, J. A., Nayfeh, A. H. & Al-Maaitah, A. A. 1992 Effect of heat transfer on the stability of compressible boundary layers. Comput. Fluids 1, 43–61.Google Scholar
Nichols, J. W., Larsson, J., Bernardini, M. & Pirozzoli, S. 2017 Stability and modal analysis of shock/boundary layer interactions. Theor. Comput. Fluid Dyn. 31, 33–50.Google Scholar
Oliviero, N. B., Kocian, T. S., Moyes, A. J. & Reed, H. L.2015 EPIC: NPSE analysis of hypersonic crossflow instability on yawed straight circular cone. In AIAA 45th Fluid Dynamics Conference. AIAA-2015-2772.Google Scholar
Park, D. & Park, S. O. 2016 Study of effect of a smooth hump on hypersonic boundary layer instability. Theor. Comput. Fluid Dyn. 30, 543–563.Google Scholar
Park, J.2012 Waves and instabilities on vortices in stratified and rotating fluids. PhD thesis, École Polytechnique.Google Scholar
Parziale, N. J., Shepherd, J. E. & Hornung, H. G. 2015 Observations of hypervelocity boundary-layer instability. J. Fluid Mech. 781, 87–112.Google Scholar
Pinna, F. & Rambaud, P. 2013 Effects of shock on hypersonic boundary layer stability. Progress Flight Phys. 5, 93–106.Google Scholar
Pralits, J. O.2003 Optimal design of natural and hybrid laminar flow control on wings. PhD thesis, Royal Institute of Technology, Stockholm, Sweden.Google Scholar
Pralits, J. O., Airiau, C., Hanifi, A. & Henningson, D. S. 2000 Sensitivity analysis using adjoint parabolized stability equations for compressible flows. Flow Turbul. Combust. 65, 321–346.Google Scholar
Pralits, J. O. & Hanifi, A. 2003 Optimization of steady suction for disturbance control on infinite swept wings. Phys. Fluids 15, 2756–2772.Google Scholar
Pralits, J. O., Hanifi, A. & Henningson, D. S. 2002 Adjoint-based optimization of steady suction for disturbance control in incompressible flows. J. Fluid Mech. 467, 129–161.Google Scholar
Reed, H. L., Perez, E., Kuehl, J., Kocian, T. & Oliviero, N.2013 Hypersonic stability and transition prediction. In AIAA 21st Fluid Dynamics Conference. AIAA-2013-2556.Google Scholar
Reed, H. L., Perez, E., Kuehl, J., Kocian, T. & Oliviero, N. 2015 Verification and validation issues in hypersonic stability and transition prediction. J. Spacecr. Rockets 52, 29–37.Google Scholar
Schlichting, H. & Gersten, K. 1979 Boundary Layer Theory, 7th edn. McGraw-Hill.Google Scholar
Schmid, P. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.Google Scholar
Schmid, P. & Brandt, L. 2014 Analysis of fluid systems: stability, receptivity, sensitivity. Appl. Mech. Rev. 66, 024803.Google Scholar
Schneider, S. P. 1999 Flight data for boundary-layer transition at hypersonic and supersonic speeds. J. Spacecr. Rockets 36, 8–20.Google Scholar
Schneider, S. P. 2001 Effect of high-speed tunnel noise on laminar-turbulent transition. J. Spacecr. Rockets 38, 323–333.Google Scholar
Schneider, S. P. 2006 Laminar-turbulent transition on reentry capsules and planetary probes. J. Spacecr. Rockets 43, 1153–1173.Google Scholar
Schneider, S. P. 2008 Effect of roughness on hypersonic boundary-layer transition. J. Spacecr. Rockets 45, 193–209.Google Scholar
Sivasubramanian, J. & Fasel, H. F. 2015 Direct numerical simulation of transition in a sharp cone boundary layer at Mach 6: fundamental breakdown. J. Fluid Mech. 768, 175–218.Google Scholar
Tumin, A. 2007 Three-dimensional spatial normal modes in compressible boundary layers. J. Fluid Mech. 586, 295–322.Google Scholar
Tumin, A. M. & Fedorov, A. V. 1983 Spatial growth of disturbances in a compressible boundary layer. J. Appl. Mech. Tech. Phys. 24 (4), 548–554.Google Scholar
Van Ingen, J. L.1956 A suggested semi-empirical method for the calculation of the boundary layer transition region. Technische Hogeschool Delft, Vliegtuigbouwkunde, Rapport VTH-74.Google Scholar
Walther, S., Airiau, C. & Bottaro, A. 2001 Optimal control of Tollmien–Schlichting waves in a developing boundary layer. Phys. Fluids 13, 2087–2096.Google Scholar
Ward, C. A. C., Wheaton, B. M., Chou, A., Berridge, D. C., Letterman, L. E., Luersen, R. P. K. & Schneider, S. P.2012 Hypersonic boundary-layer transition experiments in the Boeing/AFOSR Mach-6 Quiet Tunnel. In AIAA 50th Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. AIAA-2012-0282.Google Scholar
Yan, H., Knight, D. & Zheltovodov, A. A. 2002 Large-eddy simulation of supersonic flat-plate boundary layers using the monotonically integrated large-eddy simulation (MILES) Technique. Trans. ASME J. Fluids Engng 124, 868–875.Google Scholar