Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-17T14:42:16.177Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-organized oscillations of Leidenfrost drops

Published online by Cambridge University Press:  04 May 2018

Xiaolei Ma Open the ORCID record for Xiaolei Ma [Opens in a new window]  and
Justin C. Burton
Xiaolei Ma*
Affiliation:
Department of Physics, Emory University, Atlanta, GA 30322, USA
Justin C. Burton
Affiliation:
Department of Physics, Emory University, Atlanta, GA 30322, USA
*
†Email address for correspondence: xiaolei.ma@emory.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In the Leidenfrost effect, a thin layer of evaporated vapour forms between a liquid and a hot solid. The complex interactions between the solid, liquid and vapour phases can lead to rich dynamics even in a single Leidenfrost drop. Here we investigate the self-organized oscillations of Leidenfrost drops that are excited by a constant flow of evaporated vapour beneath the drop. We show that for small Leidenfrost drops, the frequency of a recently reported ‘breathing mode’ (Caswell, Phys. Rev. E, vol. 90, 2014, 013014) can be explained by a simple balance of gravitational and surface tension forces. For large Leidenfrost drops, azimuthal star-shaped oscillations are observed. Our previous work showed how the coupling between the rapid evaporated vapour flow and the vapour–liquid interface excites the star-shaped oscillations (Ma et al., Phys. Rev. Fluids, vol. 2, 2017, 031602). In our experiments, star-shaped oscillation modes of 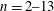$n=2{-}13$ are observed in different liquids, and the number of observed modes depends sensitively on the viscosity of the liquid. Here we expand on this work by directly comparing the oscillations with theoretical predictions, as well as show how the oscillations are initiated by a parametric forcing mechanism through pressure oscillations in the vapour layer. The pressure oscillations are driven by the capillary waves of a characteristic wavelength beneath the drop. These capillary waves can be generated by a large shear stress at the liquid–vapour interface due to the rapid flow of evaporated vapour. We also explore potential effects of thermal convection in the liquid. Although the measured Rayleigh number is significantly larger than the critical Rayleigh number, the frequency (wavelength) of the oscillations depends only on the capillary length of the liquid, and is independent of the drop radius and substrate temperature. Thus convection seems to play a minor role in Leidenfrost drop oscillations, which are mostly hydrodynamic in origin.

JFM classification

Waves/Free-surface Flows: Capillary waves Drops and Bubbles: Drops and Bubbles Waves/Free-surface Flows: Waves/Free-surface Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 846 , 10 July 2018 , pp. 263 - 291
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdelaziz, R., Disci-Zayed, D., Hedayati, M. K., Pöhls, J.-H., Zillohu, A. U., Erkartal, B., Chakravadhanula, V. S. K., Duppel, V., Kienle, L. & Elbahri, M. 2013 Green chemistry and nanofabrication in a levitated Leidenfrost drop. Nat. Commun. 4, 2400.CrossRefGoogle Scholar
Adachi, K. & Takaki, R. 1984 Vibration of a flattened drop. I. Observation. J. Phys. Soc. Japan 53, 4184–4191.CrossRefGoogle Scholar
Bain, R. M., Pulliam, C. J., Thery, F. & Cooks, R. G. 2016 Accelerated chemical reactions and organic synthesis in Leidenfrost droplets. Angew. Chem. Intl Ed. 55, 10478–10482.CrossRefGoogle ScholarPubMed
Becker, E., Hiller, W. J. & Kowalewski, T. A. 1991 Experimental and theoretical investigation of large-amplitude oscillations of liquid droplets. J. Fluid Mech. 231, 189–210.CrossRefGoogle Scholar
Bénard, H. 1901 Les tourbillons cellulaires dans une nappe liquide. – Méthodes optiques d’observation et d’enregistrement. J. Phys. Théor. Appl. 10, 254–266.Google Scholar
Bernardin, J. D. & Mudawar, I. 1999 The Leidenfrost point: experimental study and assessment of existing models. Trans. ASME J. Heat Transfer 121, 894–903.CrossRefGoogle Scholar
Biance, A.-L., Chevy, F., Clanet, C., Lagubeau, G. & Quéré, D. 2006 On the elasticity of an inertial liquid shock. J. Fluid Mech. 554, 47–66.CrossRefGoogle Scholar
Biance, A.-L., Clanet, C. & Quéré, D. 2003 Leidenfrost drops. Phys. Fluids 15, 1632–1637.CrossRefGoogle Scholar
Bouwhuis, W., Winkels, K. G., Peters, I. R., Brunet, P., van der Meer, D. & Snoeijer, J. H. 2013 Oscillating and star-shaped drops levitated by an airflow. Phys. Rev. E 88, 023017.Google ScholarPubMed
Brunet, P. & Snoeijer, J. H. 2011 Star-drops formed by periodic excitation and on an air cushion – A short review. Eur. Phys. J. Spec. Top. 192, 207–226.CrossRefGoogle Scholar
Burton, J. C., Huisman, F. M., Alison, P., Rogerson, D. & Taborek, P. 2010 Experimental and numerical investigation of the equilibrium geometry of liquid lenses. Langmuir 26, 15316–15324.CrossRefGoogle ScholarPubMed
Burton, J. C., Sharpe, A. L., van der Veen, R. C. A., Franco, A. & Nagel, S. R. 2012 Geometry of the vapor layer under a Leidenfrost drop. Phys. Rev. Lett. 109, 074301.CrossRefGoogle Scholar
Castanet, G., Caballina, O. & Lemoine, F. 2015 Drop spreading at the impact in the Leidenfrost boiling. Phys. Fluids 27, 063302.CrossRefGoogle Scholar
Caswell, T. A. 2014 Dynamics of the vapor layer below a Leidenfrost drop. Phys. Rev. E 90, 013014.Google Scholar
Chang, H.-h. & Demekhin, E. A. 2002 Complex Wave Dynamics on Thin Films. Elsevier.Google Scholar
Cousins, T. R., Goldstein, R. E., Jaworski, J. W. & Pesci, A. I. 2012 A ratchet trap for Leidenfrost drops. J. Fluid Mech. 696, 215–227.CrossRefGoogle Scholar
Driscoll, M. M. & Nagel, S. R. 2011 Ultrafast interference imaging of air in splashing dynamics. Phys. Rev. Lett. 107, 154502.CrossRefGoogle ScholarPubMed
Duchemin, L., Lister, J. R. & Lange, U. 2005 Static shapes of levitated viscous drops. J. Fluid Mech. 533, 161–170.CrossRefGoogle Scholar
Dupeux, G., Le Merrer, M., Clanet, C. & Quéré, D. 2011a Trapping Leidenfrost drops with crenelations. Phys. Rev. Lett. 107, 114503.CrossRefGoogle ScholarPubMed
Dupeux, G., Le Merrer, M., Lagubeau, G., Clanet, C., Hardt, S. & Quéré, D. 2011b Viscous mechanism for Leidenfrost propulsion on a ratchet. Europhys. Lett. 96, 58001.CrossRefGoogle Scholar
Haumesser, P.-H., Bancillon, J., Daniel, M., Perez, M. & Garandet, J.-P. 2002 High-temperature contactless viscosity measurements by the gas–film levitation technique: application to oxide and metallic glasses. Rev. Sci. Instrum. 73, 3275–3285.CrossRefGoogle Scholar
Hidalgo-Caballero, S., Escobar-Ortega, Y. & Pacheco-Vázquez, F. 2016 Leidenfrost phenomenon on conical surfaces. Phys. Rev. Fluids 1, 051902.CrossRefGoogle Scholar
Holter, N. J. & Glasscock, W. R. 1952 Vibrations of evaporating liquid drops. J. Acoust. Soc. Am. 24, 682–686.CrossRefGoogle Scholar
Ishikawa, T., Yu, J. & Paradis, P.-F. 2006 Noncontact surface tension and viscosity measurements of molten oxides with a pressurized hybrid electrostatic-aerodynamic levitator. Rev. Sci. Instrum. 77, 053901.CrossRefGoogle Scholar
Kadota, T., Tanaka, H., Segawa, D., Nakaya, S. & Yamasaki, H. 2007 Microexplosion of an emulsion droplet during Leidenfrost burning. Proc. Combust. Inst. 31, 2125–2131.CrossRefGoogle Scholar
Kolinski, J. M., Rubinstein, S. M., Mandre, S., Brenner, M. P., Weitz, D. A. & Mahadevan, L. 2012 Skating on a film of air: drops impacting on a surface. Phys. Rev. Lett. 108, 074503.CrossRefGoogle ScholarPubMed
Kumar, K. & Tuckerman, L. S. 1994 Parametric instability of the interface between two fluids. J. Fluid Mech. 279, 49–68.CrossRefGoogle Scholar
Lagubeau, G., Le Merrer, M., Clanet, C. & Quéré, D. 2011 Leidenfrost on a ratchet. Nat. Phys. 7, 395.CrossRefGoogle Scholar
Langstaff, D., Gunn, M., Greaves, G. N., Marsing, A. & Kargl, F. 2013 Aerodynamic levitator furnace for measuring thermophysical properties of refractory liquids. Rev. Sci. Instrum. 84, 124901.CrossRefGoogle ScholarPubMed
Leal, L. G. 2007 Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes. Cambridge University Press.CrossRefGoogle Scholar
Leidenfrost, J. G. 1756 De aquae communis nonnullis qualitatibus tractatus. Ovenius.Google Scholar
Lemmon, E. W., McLinden, M. O., Friend, D. G., Linstrom, P. J. & Mallard, W. G.2011 NIST chemistry WebBook, Nist standard reference database number 69 (National Institute of Standards and Technology, Gaithersburg, MD, 2011), http://webbook.nist.gov.Google Scholar
Li, J., Hou, Y., Liu, Y., Hao, C., Li, M., Chaudhury, M. K., Yao, S. & Wang, Z. 2016 Directional transport of high-temperature Janus droplets mediated by structural topography. Nat. Phys. 12, 606.CrossRefGoogle Scholar
Linke, H., Alemán, B. J., Melling, L. D., Taormina, M. J., Francis, M. J., Dow-Hygelund, C. C., Narayanan, V., Taylor, R. P. & Stout, A. 2006 Self-propelled Leidenfrost droplets. Phys. Rev. Lett. 96, 154502.CrossRefGoogle ScholarPubMed
Lister, J. R., Thompson, A. B., Perriot, A. & Duchemin, L. 2008 Shape and stability of axisymmetric levitated viscous drops. J. Fluid Mech. 617, 167–185.CrossRefGoogle Scholar
Liu, Y., Tan, P. & Xu, L. 2013 Compressible air entrapment in high-speed drop impacts on solid surfaces. J. Fluid Mech. 716, R9.CrossRefGoogle Scholar
Liu, Y., Tan, P. & Xu, L. 2015 Kelvin–Helmholtz instability in an ultrathin air film causes drop splashing on smooth surfaces. Proc. Natl Acad. Sci. USA 112, 3280–3284.CrossRefGoogle Scholar
Ma, X., Liétor-Santos, J.-J. & Burton, J. C. 2015 The many faces of a Leidenfrost drop. Phys. Fluids 27, 091109.CrossRefGoogle Scholar
Ma, X., Liétor-Santos, J.-J. & Burton, J. C. 2017 Star-shaped oscillations of Leidenfrost drops. Phys. Rev. Fluids 2, 031602.CrossRefGoogle Scholar
Mampallil, D., Eral, H. B., Staicu, A., Mugele, F. & van den Ende, D. 2013 Electrowetting-driven oscillating drops sandwiched between two substrates. Phys. Rev. E 88, 053015.Google ScholarPubMed
Maquet, L., Brandenbourger, M., Sobac, B., Biance, A.-L., Colinet, P. & Dorbolo, S. 2015 Leidenfrost drops: effect of gravity. Europhys. Lett. 110, 24001.CrossRefGoogle Scholar
Maquet, L., Sobac, B., Darbois-Texier, B., Duchesne, A., Brandenbourger, M., Rednikov, A., Colinet, P. & Dorbolo, S. 2016 Leidenfrost drops on a heated liquid pool. Phys. Rev. Fluids 1, 053902.CrossRefGoogle Scholar
Marangoni, C. 1871 Über die Ausbreitung der Tropfen einer Flüssigkeit auf der Oberfläche einer anderen. Ann. Phys. 219, 337–354.CrossRefGoogle Scholar
Marchand, A., Chan, T. S., Snoeijer, J. H. & Andreotti, B. 2012 Air entrainment by contact lines of a solid plate plunged into a viscous fluid. Phys. Rev. Lett. 108, 204501.CrossRefGoogle ScholarPubMed
Maroto, J. A., Pérez-Munuzuri, V. & Romero-Cano, M. S. 2007 Introductory analysis of Bénard–Marangoni convection. Eur. J. Phys. 28, 311.CrossRefGoogle Scholar
Miles, J. & Henderson, D. 1990 Parametrically forced surface waves. Annu. Rev. Fluid Mech. 22, 143–165.CrossRefGoogle Scholar
Miles, J. W. 1957 On the generation of surface waves by shear flows. J. Fluid Mech. 3, 185–204.CrossRefGoogle Scholar
Myers, T. G. & Charpin, J. P. F. 2009 A mathematical model of the Leidenfrost effect on an axisymmetric droplet. Phys. Fluids 21, 063101.CrossRefGoogle Scholar
Noblin, X., Buguin, A. & Brochard-Wyart, F. 2005 Triplon modes of puddles. Phys. Rev. Lett. 94, 166102.CrossRefGoogle ScholarPubMed
Noblin, X., Buguin, A. & Brochard-Wyart, F. 2009 Vibrations of sessile drops. Eur. Phys. J. Spec. Top. 166, 7–10.CrossRefGoogle Scholar
Paquier, A., Moisy, F. & Rabaud, M. 2015 Surface deformations and wave generation by wind blowing over a viscous liquid. Phys. Fluids 27, 122103.CrossRefGoogle Scholar
Paradis, P.-F. & Ishikawa, T. 2005 Surface tension and viscosity measurements of liquid and undercooled alumina by containerless techniques. Japan J. Appl. Phys. 44, 5082.CrossRefGoogle Scholar
Pomeau, Y., Le Berre, M., Celestini, F. & Frisch, T. 2012 The Leidenfrost effect: from quasi-spherical droplets to puddles. C. R. Méc. 340, 867–881.CrossRefGoogle Scholar
Quéré, D. 2013 Leidenfrost dynamics. Annu. Rev. Fluid Mech. 45, 197–215.CrossRefGoogle Scholar
Raux, P. S., Dupeux, G., Clanet, C. & Quéré, D. 2015 Successive instabilities of confined Leidenfrost puddles. Europhys. Lett. 112, 26002.CrossRefGoogle Scholar
Rayleigh, Lord 1879 On the capillary phenomena of jets. Proc. R. Soc. Lond. A 29, 71–97.Google Scholar
Rayleigh, Lord 1916 LIX. On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Phil. Mag. 32, 529–546.CrossRefGoogle Scholar
Schatz, M. F. & Neitzel, G. P. 2001 Experiments on thermocapillary instabilities. Annu. Rev. Fluid Mech. 33, 93–127.CrossRefGoogle Scholar
Shahriari, A., Wurz, J. & Bahadur, V. 2014 Heat transfer enhancement accompanying Leidenfrost state suppression at ultrahigh temperatures. Langmuir 30, 12074–12081.CrossRefGoogle ScholarPubMed
Shen, C. L., Xie, W. J. & Wei, B. 2010a Parametric resonance in acoustically levitated water drops. Phys. Lett. A 374, 2301–2304.CrossRefGoogle Scholar
Shen, C. L., Xie, W. J. & Wei, B. 2010b Parametrically excited sectorial oscillation of liquid drops floating in ultrasound. Phys. Rev. E 81, 046305.Google ScholarPubMed
Shirota, M., van Limbeek, M. A. J., Sun, C., Prosperetti, A. & Lohse, D. 2016 Dynamic Leidenfrost effect: relevant time and length scales. Phys. Rev. Lett. 116, 064501.CrossRefGoogle ScholarPubMed
Smith, W. R. 2010 Modulation equations for strongly nonlinear oscillations of an incompressible viscous drop. J. Fluid Mech. 654, 141–159.CrossRefGoogle Scholar
Snezhko, A., Jacob, E. B. & Aranson, I. S. 2008 Pulsating–gliding transition in the dynamics of levitating liquid nitrogen droplets. New J. Phys. 10, 043034.CrossRefGoogle Scholar
Snoeijer, J. H., Brunet, P. & Eggers, J. 2009 Maximum size of drops levitated by an air cushion. Phys. Rev. E 79, 036307.Google ScholarPubMed
Sobac, B., Rednikov, A., Dorbolo, S. & Colinet, P. 2014 Leidenfrost effect: Accurate drop shape modeling and refined scaling laws. Phys. Rev. E 90, 053011.Google ScholarPubMed
Sobac, B., Rednikov, A., Dorbolo, S. & Colinet, P. 2017 Self-propelled Leidenfrost drops on a thermal gradient: a theoretical study. Phys. Fluids 29, 082101.CrossRefGoogle Scholar
Soto, D., Lagubeau, G., Clanet, C. & Quéré, D. 2016 Surfing on a herringbone. Phys. Rev. Fluids 1, 013902.CrossRefGoogle Scholar
Strier, D. E., Duarte, A. A., Ferrari, H. & Mindlin, G. B. 2000 Nitrogen stars: morphogenesis of a liquid drop. Physica A 283, 261–266.CrossRefGoogle Scholar
Takaki, R. & Adachi, K. 1985 Vibration of a flattened drop. II. Normal mode analysis. J. Phys. Soc. Japan 54, 2462–2469.CrossRefGoogle Scholar
Talari, V., Behar, P., Lu, Y., Haryadi, E. & Liu, D. 2018 Leidenfrost drops on micro/nanostructured surfaces. Front. Energy 12, 22–42.CrossRefGoogle Scholar
Terwagne, D. & Bush, J. W. M. 2011 Tibetan singing bowls. Nonlinearity 24, R51.CrossRefGoogle Scholar
Tokugawa, N. & Takaki, R. 1994 Mechanism of self-induced vibration of a liquid drop based on the surface tension fluctuation. J. Phys. Soc. Japan 63, 1758–1768.CrossRefGoogle Scholar
Tran, T., Staat, H. J. J., Prosperetti, A., Sun, C. & Lohse, D. 2012 Drop impact on superheated surfaces. Phys. Rev. Lett. 108, 036101.CrossRefGoogle ScholarPubMed
Trinh, P. H., Kim, H., Hammoud, N., Howell, P. D., Chapman, S. J. & Stone, H. A. 2014 Curvature suppresses the Rayleigh–Taylor instability. Phys. Fluids 26, 051704.CrossRefGoogle Scholar
Vakarelski, I. U., Chan, D. Y. C. & Thoroddsen, S. T. 2014 Leidenfrost vapour layer moderation of the drag crisis and trajectories of superhydrophobic and hydrophilic spheres falling in water. Soft Matt. 10, 5662–5668.CrossRefGoogle ScholarPubMed
Vakarelski, I. U., Marston, J. O., Chan, D. Y. C. & Thoroddsen, S. T. 2011 Drag reduction by Leidenfrost vapor layers. Phys. Rev. Lett. 106, 214501.CrossRefGoogle ScholarPubMed
Vakarelski, I. U., Patankar, N. A., Marston, J. O., Chan, D. Y. C. & Thoroddsen, S. T. 2012 Stabilization of Leidenfrost vapour layer by textured superhydrophobic surfaces. Nature 489, 274.CrossRefGoogle ScholarPubMed
Van Dam, H. 1992 Physics of nuclear reactor safety. Rep. Prog. Phys. 55, 2025.Google Scholar
Waitukaitis, S. R., Zuiderwijk, A., Souslov, A., Coulais, C. & van Hecke, M. 2017 Coupling the Leidenfrost effect and elastic deformations to power sustained bouncing. Nat. Phys. 13 (11), 1095.CrossRefGoogle Scholar
Wong, C. Y. H., Adda-Bedia, M. & Vella, D. 2017 Non-wetting drops at liquid interfaces: from liquid marbles to Leidenfrost drops. Soft Matt. 13, 5250–5260.CrossRefGoogle ScholarPubMed
Xu, L., Zhang, W. W. & Nagel, S. R. 2005 Drop splashing on a dry smooth surface. Phys. Rev. Lett. 94, 184505.CrossRefGoogle ScholarPubMed
Xu, X. & Qian, T. 2013 Hydrodynamics of Leidenfrost droplets in one-component fluids. Phys. Rev. E 87, 043013.Google ScholarPubMed
Yoshiyasu, N., Matsuda, K. & Takaki, R. 1996 Self-induced vibration of a water drop placed on an oscillating plate. J. Phys. Soc. Japan 65, 2068–2071.CrossRefGoogle Scholar
Zeisel, A., Stiassnie, M. & Agnon, Y. 2008 Viscous effects on wave generation by strong winds. J. Fluid Mech. 597, 343–369.CrossRefGoogle Scholar
Zhang, X. 1995 Capillary-gravity and capillary waves generated in a wind wave tank: observations and theories. J. Fluid Mech. 289, 51.CrossRefGoogle Scholar