Hostname: page-component-77c89778f8-fv566 Total loading time: 0 Render date: 2024-07-17T17:12:28.080Z Has data issue: false hasContentIssue false
  • English
  • Français

Reappraisal of the velocity derivative flatness factor in various turbulent flows

Published online by Cambridge University Press:  21 May 2018

S. L. Tang Open the ORCID record for S. L. Tang [Opens in a new window] ,
R. A. Antonia ,
L. Djenidi Open the ORCID record for L. Djenidi [Opens in a new window] ,
L. Danaila  and
Y. Zhou
S. L. Tang*
Affiliation:
Institute for Turbulence–Noise–Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055, PR China Digital Engineering Laboratory of Offshore Equipment, Shenzhen 518055, PR China
R. A. Antonia
Affiliation:
School of Engineering, University of Newcastle, NewcastleNSW 2308, Australia
L. Djenidi
Affiliation:
School of Engineering, University of Newcastle, NewcastleNSW 2308, Australia
L. Danaila
Affiliation:
CORIA, CNRS, UMR 6614, Université de Rouen Normandie, 76801 Saint Etienne du Rouvray, France
Y. Zhou
Affiliation:
Institute for Turbulence–Noise–Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055, PR China Digital Engineering Laboratory of Offshore Equipment, Shenzhen 518055, PR China
*
†Email address for correspondence: shunlin.tang88@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We first analytically show, starting with the Navier–Stokes equations, that the value of the derivative flatness is controlled by pressure diffusion of energy, viscous destructive effects and large-scale effects (decay and/or production). The latter two terms tend to zero when the Taylor-microscale Reynolds number 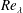$Re_{\unicode[STIX]{x1D706}}$ is sufficiently large. We argue that the pressure-diffusion term should also tend to a constant at large 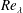$Re_{\unicode[STIX]{x1D706}}$. Available data for the velocity derivative flatness, 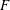$F$, in different turbulent flows are re-examined and interpreted in the light of the finite-Reynolds-number effect. It is found that 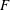$F$ can differ from flow to flow at moderate 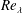$Re_{\unicode[STIX]{x1D706}}$; for a given flow, 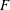$F$ may also depend on the initial conditions. The data for 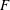$F$ in various flows, e.g. along the axis in the far field of plane and circular jets, and grid turbulence, show that it approaches a constant, with a value slightly larger than 10, when 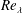$Re_{\unicode[STIX]{x1D706}}$ is sufficiently large. This behaviour for 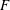$F$ is supported, at least qualitatively, by our analytical considerations. The constancy of 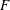$F$ at large 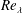$Re_{\unicode[STIX]{x1D706}}$ violates the refined similarity hypothesis introduced by Kolmogorov (J. Fluid Mech., vol. 13, 1962, pp. 82–85) to account for the intermittency of the energy dissipation rate. It is not, however, inconsistent with Kolmogorov’s original similarity hypothesis (Dokl. Akad. Nauk SSSR, vol. 30, 1941, pp. 299–303), although we contend that the power-law relation 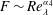$F\sim Re_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FC}_{4}}$ (Kolmogorov 1962), which is widely accepted in the literature, has in reality been almost invariably used to ‘model’ the finite-Reynolds-number effect for the laboratory data and has been strongly influenced by the weighting given to the atmospheric surface layer data. The inclusion of the latter data has misled previous investigations of how 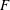$F$ varies with 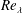$Re_{\unicode[STIX]{x1D706}}$.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 847 , 25 July 2018 , pp. 244 - 265
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A., Anselmet, F. & Chambers, A. J. 1986 Assessment of local isotropy using measurements in a turbulent plane jet. J. Fluid Mech. 163, 365–391.CrossRefGoogle Scholar
Antonia, R. A., Chambers, A. J. & Satyaprakash, B. R. 1981 Reynolds number dependence of high-order moments of the streamwise turbulent velocity derivative. Boundary-Layer Meteorol. 21, 159–171.CrossRefGoogle Scholar
Antonia, R. A., Djenidi, L. & Danaila, L. 2014 Collapse of the turbulent dissipation range on Kolmogorov scales. Phys. Fluids 26, 045105.CrossRefGoogle Scholar
Antonia, R. A., Djenidi, L., Danaila, L. & Tang, S. L. 2017 Small scale turbulence and the finite Reynolds number effect. Phys. Fluids 29 (2), 020715.Google Scholar
Antonia, R. A., Satyaprakash, B. R. & Hussain, A. K. M. F. 1982 Statistics of fine-scale velocity in turbulent plane and circular jets. J. Fluid Mech. 119, 55–89.CrossRefGoogle Scholar
Antonia, R. A., Tang, S. L., Djenidi, L. & Danaila, L. 2015 Boundedness of the velocity derivative skewness in various turbulent flows. J. Fluid Mech. 781, 727–744.CrossRefGoogle Scholar
Antonia, R. A., Zhou, T. & Romano, G. P. 2002 Small-scale turbulence characteristics of two-dimensional bluff body wakes. J. Fluid Mech. 459, 67–92.CrossRefGoogle Scholar
Batchelor, G. K. & Townsend, A. A. 1947 Decay of vorticity in isotropic turbulence. Proc. R. Soc. Lond. A 190, 534–550.Google Scholar
Batchelor, G. K. & Townsend, A. A. 1949 The nature of turbulent motion at large wave-numbers. Proc. R. Soc. Lond. A 199, 238–255.Google Scholar
Belin, F., Maurer, J., Tabeling, P. & Willaime, H. 1997 Velocity gradient distributions in fully developed turbulence: experimental study. Phys. Fluids 9, 3843–3850.Google Scholar
Burattini, P., Lavoie, P. & Antonia, R. A. 2008 Velocity derivative skewness in isotropic turbulence and its measurement with hot wires. Exp. Fluids 45, 523–535.Google Scholar
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Dimotakis, P. E. 2000 The mixing transition in turbulent flows. J. Fluid Mech. 409, 69–98.Google Scholar
Djenidi, L., Antonia, R. A. & Danaila, L. 2017a Self-preservation relation to the Kolmogorov similarity hypotheses. Phys. Rev. Fluids 2, 054606.CrossRefGoogle Scholar
Djenidi, L., Antonia, R. A., Danaila, L. & Tang, S. L. 2017b A note on the velocity derivative flatness factor in decaying HIT. Phys. Fluids 29, 051702.CrossRefGoogle Scholar
Djenidi, L., Antonia, R. A., Talluru, M. K. & Abe, H. 2017c Skewness and flatness factors of the longitudinal velocity derivative in wall-bounded flows. Phys. Rev. Fluids 2, 064608.Google Scholar
Friehe, C. A., Van Atta, C. W. & Gibson, C. H. 1971 Jet turbulence: dissipation rate measurements and correlations. AGARD Turbul. Shear Flows 18, 1–7.Google Scholar
Gauding, M.2014 Statistics and scaling laws of turbulent scalar mixing at high Reynolds numbers. PhD thesis, RWTH Aachen University.Google Scholar
Gibson, C. H., Stegen, G. R. & Williams, R. B. 1970 Statistics of the fine structure of turbulent velocity and temperature fields at high Reynolds number. J. Fluid Mech. 41, 153–167.Google Scholar
Gotoh, T., Fukayama, D. & Nakano, T. 2002 Velocity field statistics in homogeneous steady turbulence obtained using a high-resolution direct numerical simulation. Phys. Fluids 14, 1065–1081.CrossRefGoogle Scholar
Gotoh, T. & Nakano, T. 2003 Role of pressure in turbulence. J. Stat. Phys. 113, 855–874.CrossRefGoogle Scholar
Gylfason, A., Ayyalasomayajula, S. & Warhaft, Z. 2004 Intermittency, pressure and acceleration statistics from hot-wire measurements in wind-tunnel turbulence. J. Fluid Mech. 501, 213–229.Google Scholar
Hill, R. J. 2001 Equations relating structure functions of all orders. J. Fluid Mech. 434, 379–388.Google Scholar
Hill, R. J. 2002 Scaling of acceleration in locally isotropic turbulence. J. Fluid Mech. 452, 361–370.CrossRefGoogle Scholar
Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.Google Scholar
Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2003 Spectra of energy dissipation, enstrophy and pressure by high-resolution direct numerical simulations of turbulence in a periodic box. J. Phys. Soc. Japan 72, 983–986.Google Scholar
Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2007 Small-scale statistics in high-resolution direct numerical simulation of turbulence: Reynolds number dependence of one-point velocity gradient statistics. J. Fluid Mech. 592, 335–366.Google Scholar
Jimenez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.CrossRefGoogle Scholar
Kahalerras, H., Malecot, Y. & Gagne, Y. 1998 Intermittency and Reynolds number. Phys. Fluids 10, 910–921.CrossRefGoogle Scholar
Kerr, R. M. 1985 Higher-order derivative correlations and the alignment of small-scale structures in isotropic numerical turbulence. J. Fluid Mech. 153, 31–58.CrossRefGoogle Scholar
Kim, J. & Antonia, R. A. 1993 Isotropy of the small-scales of turbulence at small Reynolds numbers. J. Fluid Mech. 251, 219–238.Google Scholar
Kolmogorov, A. N. 1941a Dissipation of energy in the locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32, 19–21.Google Scholar
Kolmogorov, A. N. 1941b Local structure of turbulence in an incompressible fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299–303.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.Google Scholar
Kraichnan, R. H. 1991 Turbulent cascade and intermittency growth. Proc. R. Soc. Lond. A 434, 65–78.Google Scholar
Kuo, A. Y.-S. & Corrsin, S. 1971 Experiments on internal intermittency and fine-structure distribution functions in fully turbulent fluid. J. Fluid Mech. 50 (02), 285–319.CrossRefGoogle Scholar
Metzger, M., McKeon, B. J. & Holmes, H. 2007 The near-neutral atmospheric surface layer: turbulence and non-stationarity. Phil. Trans. R. Soc. Lond. A 365, 859–876.Google Scholar
Mi, J., Xu, M. & Zhou, T. 2013 Reynolds number influence on statistical behaviors of turbulence in a circular free jet. Phys. Fluids 25, 075101.Google Scholar
Moisy, F., Tabeling, P. & Willaime, H. 1999 Kolmogorov equation in a fully developed turbulence experiment. Phys. Rev. Lett. 82 (20), 3994–3997.Google Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.Google Scholar
Pearson, B. R. & Antonia, R. A. 2001 Reynolds-number dependence of turbulent velocity and pressure increments. J. Fluid Mech. 444, 343–382.Google Scholar
Pearson, B. R. & Krogstad, P. A. 2001 Further evidence for a transition in small-scale turbulence. In 14th Australasian Fluid Mechanics Conference, Adelaide.Google Scholar
Qian, J. 1983 Variational approach to the closure problem of turbulence theory. Phys. Fluids 26 (8), 2098–2104.Google Scholar
Qian, J. 1986 A closure theory of intermittency of turbulence. Phys. Fluids 29, 2165.Google Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy of turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.CrossRefGoogle Scholar
Shen, X. & Warhaft, Z. 2000 The anisotropy of the small scale structure in high Reynolds number (R 𝜆 ∼ 1000) turbulent shear flow. Phys. Fluids 12, 2976–2989.CrossRefGoogle Scholar
Sinhuber, M., Bodenschatz, E. & Bewley, G. P. 2015 Decay of turbulence at high Reynolds numbers. Phys. Rev. Lett. 114 (3), 034501.Google Scholar
Sreenivasan, K. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.Google Scholar
Sreenivasan, K. R. 1995 Small-scale intermittency in turbulence. In Proc. Twelfth Australasian Fluid Mechanics Conference, University of Sydney, Australia, pp. 549–556.Google Scholar
Tabeling, P. & Willaime, H. 2002 Transition at dissipative scales in large Reynolds number turbulence. Phys. Rev. E 65, 066301.Google Scholar
Tabeling, P., Zocchi, G., Belin, F., Maurer, J. & Willaime, H. 1996 Probability density functions, skewness, and flatness in large Reynolds number turbulence. Phys. Rev. E 53, 1613–1621.Google Scholar
Tang, S. L., Antonia, R. A., Danaila, L., Djenidi, L., Zhou, T. & Zhou, Y. 2016 Towards local isotropy of higher-order statistics in the intermediate wake. Exp. Fluids 57, 111.Google Scholar
Tang, S. L., Antonia, R. A., Djenidi, L., Abe, H., Zhou, T., Danaila, L. & Zhou, Y. 2015a Transport equation for the mean turbulent energy dissipation rate on the centreline of a fully developed channel flow. J. Fluid Mech. 777, 151–177.Google Scholar
Tang, S. L., Antonia, R. A., Djenidi, L. & Zhou, Y. 2015b Transport equation for the isotropic turbulent energy dissipation rate in the far-wake of a circular cylinder. J. Fluid Mech. 784, 109–129.Google Scholar
Thiesset, F., Antonia, R. A. & Djenidi, L. 2014 Consequences of self-preservation on the axis of a turbulent round jet. J. Fluid Mech. 748, R2.Google Scholar
Thiesset, F., Danaila, L. & Antonia, R. A. 2013 Dynamical effect of the total strain induced by the coherent motion on local isotropy in a wake. J. Fluid Mech. 720, 393–423.CrossRefGoogle Scholar
Tong, C. & Warhaft, Z. 1994 On passive scalar derivative statistics in grid turbulence. Phys. Fluids 6 (6), 2165–2176.Google Scholar
Van Atta, C. W. & Antonia, R. A. 1980 Reynolds number dependence of skewness and flatness factors of turbulent velocity derivatives. Phys. Fluids 23, 252–257.Google Scholar
Wang, L.-P., Chen, S., Brasseur, J. G. & Wyngaard, J. C. 1996 Examination of hypotheses in Kolmogorov refined turbulence theory through high-resolution simulations. Part 1. Velocity field. J. Fluid Mech. 309, 113–156.CrossRefGoogle Scholar
Wyngaard, J. C. 2010 Turbulence in the Atmosphere. Cambridge University Press.Google Scholar
Wyngaard, J. C. & Tennekes, H. 1970 Measurements of the small-scale structure of turbulence at moderate Reynolds numbers. Phys. Fluids 13, 1962–1969.CrossRefGoogle Scholar
Xu, G., Antonia, R. A. & Rajagopalan, S. 2001 Sweeping decorrelation hypothesis in a turbulent round jet. Fluid Dyn. Res. 28 (5), 311–321.Google Scholar
Yeung, P. K., Donzis, D. A. & Sreenivasan, K. R. 2005 High-Reynolds-number simulation of turbulent mixing. Phys. Fluids 17, 081703.Google Scholar
Yeung, P. K. & Zhou, Y. 1997 Universality of the Kolmogorov constant in numerical simulations of turbulence. Phys. Rev. E 56, 1746–1752.Google Scholar
Zhou, T. & Antonia, R. A. 2000 Reynolds number dependence of the small-scale structure of grid turbulence. J. Fluid Mech. 406, 81–107.Google Scholar
Zhou, T., Antonia, R. A. & Chua, L. P. 2005 Flow and Reynolds number dependencies of one-dimensional vorticity fluctuations. J. Turbul. 6, N28.CrossRefGoogle Scholar