Hostname: page-component-788cddb947-jbjwg Total loading time: 0 Render date: 2024-10-19T06:19:11.738Z Has data issue: false hasContentIssue false
  • English
  • Français

The rapid-rotation limit of the neutral curve for Taylor–Couette flow

Published online by Cambridge University Press:  27 October 2016

Kengo Deguchi
Kengo Deguchi*
Affiliation:
School of Mathematical Sciences, Monash University, VIC 3800, Australia
*
†Email address for correspondence: Kengo.Deguchi@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

An asymptotic theory is developed for the linear stability curve of rapidly rotating Taylor–Couette flow. The analytic curve obtained by the theory excellently explains the limiting Navier–Stokes stability result for general disturbances. When the cylinders are corotating, the asymptotic theory describes the gap between the neutral curve and the Rayleigh stability criterion. For the case when the cylinders are counter-rotating, it is found that, along the stability boundary, the Reynolds number based on the inner cylinder speed is proportional to that based on the outer cylinder speed to the power of 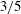$3/5$.

JFM classification

Aerodynamics: High-speed flow
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 808 , 10 December 2016 , R2
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.CrossRefGoogle Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Boyd, J. P. 2001 Chebyshev and Fourier Spectral Methods. Dover.Google Scholar
Deguchi, K., Hall, P. & Walton, A. G. 2013 The emergence of localized vortex–wave interaction states in plane Couette flow. J. Fluid Mech. 721, 58–85.CrossRefGoogle Scholar
Deguchi, K., Meseguer, A. & Mellibovsky, F. 2014 Subcritical equilibria in Taylor–Couette flow. Phys. Rev. Lett. 112, 184502.Google Scholar
Deguchi, K. & Nagata, M. 2011 Bifurcations and instabilities in sliding Couette flow. J. Fluid Mech. 678, 156–178.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Dutcher, C. S. & Mullar, S. J. 2007 Explicit analytic formulas for Newtonian Taylor–Couette primary instabilities. Phys. Rev. E 75, 047301.Google Scholar
Esser, A. & Grossmann, S. 1996 Analytic expression for Taylor–Couette stability boundary. Phys. Fluids 8, 1814–1819.Google Scholar
Grossmann, S., Lohse, D. & Sun, C. 2016 High-Reynolds number Taylor–Couette turbulence. Annu. Rev. Fluid Mech. 48, 53–80.Google Scholar
Hall, P. 1982 Taylor–Görtler vortices in fully developed or boundary layer flows: linear theory. J. Fluid Mech. 124, 475–494.Google Scholar
Hall, P. 1983 The linear development of Görtler vortices in growing boundary layers. J. Fluid Mech. 130, 41–58.CrossRefGoogle Scholar
Johnston, J. P., Halleen, M. & Lezius, D. K. 1972 Effects of spanwise rotation on the structure of two-dimensional fully developed turbulent channel flow. J. Fluid Mech. 56, 533–557.CrossRefGoogle Scholar
Langford, W. F., Tagg, R., Koestlich, E. J., Swinney, H. L. & Golubitsky, M. 1988 Primary instabilities and bicriticality in flow between counter-rotating cylinders. Phys. Fluids 31, 776–785.Google Scholar
Nagata, M. 1986 Bifurcations in Couette flow between almost corotating cylinders. J. Fluid Mech. 169, 229–250.Google Scholar
Ostilla, R., Stevens, R. J. A. M., Grossmann, S., Verzicco, R. & Lohse, D. 2013 Optimal Taylor–Couette flow: direct numerical simulations. J. Fluid Mech. 719, 14–46.Google Scholar
Rayleigh, Lord 1917 On the dynamics of revolving fluids. Proc. R. Soc. Lond. A 93, 148–154.Google Scholar
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. A 223, 289–343.Google Scholar
Veronis, G. 1970 The analogy between rotating and stratified fluids. Annu. Rev. Fluid Mech. 2, 37–66.Google Scholar