Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-17T21:33:52.045Z Has data issue: false hasContentIssue false
  • English
  • Français

Radiative instability of an anticyclonic vortex in a stratified rotating fluid

Published online by Cambridge University Press:  27 July 2012

Junho Park  and
Paul Billant
Junho Park*
Affiliation:
LadHyX, CNRS, École Polytechnique, F-91128 Palaiseau CEDEX, France
Paul Billant
Affiliation:
LadHyX, CNRS, École Polytechnique, F-91128 Palaiseau CEDEX, France
*
†Email address for correspondence: junho.park@ladhyx.polytechnique.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In strongly stratified fluids, an axisymmetric vertical columnar vortex is unstable because of a spontaneous radiation of internal waves. The growth rate of this radiative instability is strongly reduced in the presence of a cyclonic background rotation 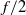and is smaller than the growth rate of the centrifugal instability for anticyclonic rotation, so it is generally expected to affect vortices in geophysical flows only if the Rossby number 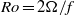is large (where 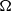is the angular velocity of the vortex). However, we show here that an anticyclonic Rankine vortex with low Rossby number in the range 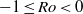, which is centrifugally stable, is unstable to the radiative instability when the azimuthal wavenumber 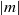is larger than 2. Its growth rate for 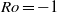is comparable to the values reported in non-rotating stratified fluids. In the case of continuous vortex profiles, this new radiative instability is shown to occur if the potential vorticity of the base flow has a sufficiently steep radial profile. The most unstable azimuthal wavenumber is inversely proportional to the steepness of the vorticity jump. The properties and mechanism of the instability are explained by asymptotic analyses for large wavenumbers.

JFM classification

Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows Vortex Flows: Vortex instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 707 , 25 September 2012 , pp. 381 - 392
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abramowitz, M. & Stegun, I. A. 1965 Handbook of Mathematical Functions. Dover.Google Scholar
2. Antkowiak, A. & Brancher, P. 2007 On vortex rings around vortices: an optimal mechanism. J. Fluid Mech. 578, 295–304.CrossRefGoogle Scholar
3. Bender, C. M. & Orszag, S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers. McGraw-Hill.Google Scholar
4. Billant, P. & Chomaz, J.-M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13, 1645.CrossRefGoogle Scholar
5. Billant, P. & Le Dizès, S. 2009 Waves on a columnar vortex in a strongly stratified fluid. Phys. Fluids 21, 106602.CrossRefGoogle Scholar
6. Bower, A., Armi, L. & Ambar, I. 1997 Lagrangian observations of Meddy formation during a Mediterranean undercurrent seeding experiment. J. Phys. Oceanogr. 27, 2545–2575.2.0.CO;2>CrossRefGoogle Scholar
7. Broadbent, E. & Moore, D. W. 1979 Acoustic destabilization of vortices. Phil. Trans. R. Soc. Lond. Ser. A 290, 353.Google Scholar
8. Candelier, J., Le Dizès, S. & Millet, C. 2012 Inviscid instability of a stably stratified compressible boundary layer on an inclined surface. J. Fluid Mech. 694, 524–539.CrossRefGoogle Scholar
9. Ford, R. 1994 The instability of an axisymmetric vortex with monotonic potential vorticity in rotating shallow water. J. Fluid Mech. 280, 303–334.CrossRefGoogle Scholar
10. Kloosterziel, R. C. & van Heijst, G. J. F. 1991 An experimental study of unstable barotropic vortices in a rotating fluid. J. Fluid Mech. 223, 1–24.CrossRefGoogle Scholar
11. Le Dizès, S. & Billant, P. 2009 Radiative instability in stratified vortices. Phys. Fluids 21, 096602.CrossRefGoogle Scholar
12. Le Dizès, S. & Lacaze, L. 2005 An asymptotic description of vortex Kelvin modes. J. Fluid Mech. 542, 69–96.CrossRefGoogle Scholar
13. Le Dizès, S. & Riedinger, X. 2010 The strato-rotational instability of Taylor–Couette and Keplerian flows. J. Fluid Mech. 660, 147–161.CrossRefGoogle Scholar
14. Ménesguen, C., Hua, B. L., Papenberg, C., Klaeschen, D., Géli, L. & Hobbs, R. 2009 Effect of bandwidth on seismic imaging of rotating stratified turbulence surrounding an anticyclonic eddy from field data and numerical simulations. Geophys. Res. Lett. 36, L00D05.CrossRefGoogle Scholar
15. Riedinger, X., Le Dizès, S. & Meunier, P. 2010 Viscous instability of a Lamb–Oseen vortex in a stratified fluid. J. Fluid Mech. 645, 255–278.CrossRefGoogle Scholar
16. Riedinger, X., Le Dizès, S. & Meunier, P. 2011 Radiative instability of the flow around a rotating cylinder in a stratified fluid. J. Fluid Mech. 672, 130–146.CrossRefGoogle Scholar
17. Schecter, D. A. 2008 The spontaneous imbalance of an atmospheric vortex at high Rossby number. J. Atmos. Sci. 65, 2498.CrossRefGoogle Scholar
18. Schecter, D. A. & Montgomery, M. T. 2004 Damping and pumping of a vortex Rossby wave in a monotonic cyclone: critical layer stirring versus inertia–buoyancy wave emission. Phys. Fluids 26 (5), 1334.CrossRefGoogle Scholar
19. Schecter, D. A. & Montgomery, M. T. 2006 Conditions that inhibit the spontaneous radiation of spiral inertia–gravity waves from an intense mesoscale cyclone. J. Atmos. Sci. 63, 435.CrossRefGoogle Scholar
20. Smyth, W. D. & McWilliams, J. C. 1998 Instability of an axisymmetric vortex in a stably stratified, rotating environment. Theor. Comput. Fluid Dyn. 11, 305–322.CrossRefGoogle Scholar
21. Vanneste, J. & Yavneh, I. 2004 Exponentially small inertia–gravity waves and the breakdown of quasigeostrophic balance. J. Atmos. Sci. 61, 211–223.2.0.CO;2>CrossRefGoogle Scholar
22. Vanneste, J. & Yavneh, I. 2007 Unbalanced instabilities of rapidly rotating stratified shear flows. J. Fluid Mech. 584, 373–396.CrossRefGoogle Scholar