Article contents
Puffing in planar buoyant plumes: BiGlobal instability analysis and experiments
Published online by Cambridge University Press: 28 January 2019
Abstract
The present study investigates the puffing behaviour of planar buoyant plumes by employing linear BiGlobal stability analysis and experiments. The BiGlobal instability characteristics of two-dimensional plumes have been explored using stability analysis and compared with the puffing behaviour of both rectangular plumes and square plumes obtained from experiments. In the parameter space investigated, which spans a Richardson number range 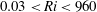 $0.03<Ri<960$, instability analysis reveals that planar plumes exhibit BiGlobal instability only for varicose perturbations, while they remain stable for sinuous perturbations. The BiGlobal frequency and growth rates of the unstable varicose mode are used to obtain Strouhal number correlation and stability curves. An investigation into the effect of the spanwise wavenumber on BiGlobal instability indicates that planar plumes are more unstable to two-dimensional perturbations than to three-dimensional perturbations. An increase in the spanwise wavenumber tends to stabilize planar plumes without affecting their oscillation frequencies. Experiments suggest that the puffing frequencies in rectangular plumes closely follow the power law obtained from two-dimensional instability analysis while exhibiting a weaker dependence on inlet aspect ratio. To further explore the effect of aspect ratio on puffing behaviour, experiments have been carried out in plumes of aspect ratio 1, i.e. square plumes. Square plumes are found to be more stable and to exhibit higher puffing frequencies than rectangular plumes. The reasons for these differences in puffing dynamics between rectangular and square plumes have been explored from the phase-locked streamwise and spanwise flow visualizations. In addition to puffing, spanwise visualizations in both rectangular and square plumes show the presence of secondary flows at their corners, similar to their constant-density jet counterparts. Finally, from experiments, we deduced a new universal puffing frequency correlation with the hydraulic diameter as the length scale which eliminates the aspect ratio dependence, and is valid for both square and low-aspect-ratio rectangular plumes.
$0.03<Ri<960$, instability analysis reveals that planar plumes exhibit BiGlobal instability only for varicose perturbations, while they remain stable for sinuous perturbations. The BiGlobal frequency and growth rates of the unstable varicose mode are used to obtain Strouhal number correlation and stability curves. An investigation into the effect of the spanwise wavenumber on BiGlobal instability indicates that planar plumes are more unstable to two-dimensional perturbations than to three-dimensional perturbations. An increase in the spanwise wavenumber tends to stabilize planar plumes without affecting their oscillation frequencies. Experiments suggest that the puffing frequencies in rectangular plumes closely follow the power law obtained from two-dimensional instability analysis while exhibiting a weaker dependence on inlet aspect ratio. To further explore the effect of aspect ratio on puffing behaviour, experiments have been carried out in plumes of aspect ratio 1, i.e. square plumes. Square plumes are found to be more stable and to exhibit higher puffing frequencies than rectangular plumes. The reasons for these differences in puffing dynamics between rectangular and square plumes have been explored from the phase-locked streamwise and spanwise flow visualizations. In addition to puffing, spanwise visualizations in both rectangular and square plumes show the presence of secondary flows at their corners, similar to their constant-density jet counterparts. Finally, from experiments, we deduced a new universal puffing frequency correlation with the hydraulic diameter as the length scale which eliminates the aspect ratio dependence, and is valid for both square and low-aspect-ratio rectangular plumes.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 11
- Cited by


