Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T23:13:36.187Z Has data issue: false hasContentIssue false
  • English
  • Français

Potential vorticity redistribution by localised transient forcing in the shallow-water model

Published online by Cambridge University Press:  03 August 2018

Michael C. Haigh Open the ORCID record for Michael C. Haigh [Opens in a new window]  and
Pavel S. Berloff
Michael C. Haigh*
Affiliation:
Department of Mathematics, Imperial College London, Huxley Building, 180 Queen’s Gate, London SW7 2AZ, UK
Pavel S. Berloff
Affiliation:
Department of Mathematics, Imperial College London, Huxley Building, 180 Queen’s Gate, London SW7 2AZ, UK
*
†Email address for correspondence: m.haigh15@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

This study is motivated by the need to develop stochastic parameterisations for representing the effects of mesoscale oceanic eddies in non-eddy-resolving and eddy-permitting ocean circulation models. A necessary logical step on the way to such parameterisations is the understanding of flow responses to spatially stationary and localised, time-dependent ‘plunger’ forcings intended to represent transient eddy flux divergences. Specifically, this study develops an understanding of the plunger-induced convergence of potential vorticity (PV) fluxes using the linearised single-layer shallow-water model. Time-periodic solutions are obtained and the ‘footprint’, defined as the time-mean, quasi-linear PV flux convergence, quantifies the cumulative PV redistribution induced by the plunger. Using the footprint, the equivalent eddy flux (EEF) is defined such that it succinctly quantifies the extent of the PV redistribution, and its dependencies on the forcing latitude and the background flow are examined in detail. For a uniform background flow the EEF is positive for all forcing latitudes, corresponding to net-poleward PV flux convergence, as expected by current theory of 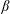$\unicode[STIX]{x1D6FD}$-plane Rossby waves. The EEF also has a robust dependence on the direction and magnitude of a uniform background flow, which is a useful quality for the EEF to provide a basis for a parameterisation of eddy PV fluxes. We also examine the PV redistribution due to forcing on top of a Gaussian jet background flow and find that forcing proximity to the jet core is the primary factor in determining whether the jet is sharpened or broadened.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Ocean circulation Geophysical and Geological Flows: Shallow water flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 852 , 10 October 2018 , pp. 199 - 225
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arai, M. & Yamagata, T. 1994 Asymmetric evolution of eddies in rotating shallow water. Chaos 163 (2), 163–175.Google Scholar
Berloff, P. 2005a On dynamically consistent eddy fluxes. Dyn. Atmos. Oceans 38, 123–146.Google Scholar
Berloff, P. 2005b On rectification of randomly forced flows. J. Mar. Res. 31, 497–527.Google Scholar
Berloff, P. 2005c Random-forcing model of the mesoscale oceanic eddies. J. Fluid. Mech. 529, 71–95.Google Scholar
Berloff, P. 2015 Dynamically consistent parameterization of mesoscale eddies. Part I. Simple model. Ocean Model. 87, 1–19.Google Scholar
Berloff, P. 2016 Dynamically consistent parameterization of mesoscale eddies. Part II. Eddy fluxes and diffusivity from transient impulses. Fluids 22, 1–25.Google Scholar
Berloff, P. 2018 Dynamically consistent parameterization of mesoscale eddies. Part III. Deterministic approach. Ocean Model. 127, 1–15.Google Scholar
Berloff, P. & Kamenkovich, I. 2013a On spectral analysis of mesoscale eddies. Part I. Linear analysis. J. Phys. Oceanogr. 43, 2505–2527.Google Scholar
Berloff, P. & Kamenkovich, I. 2013b On spectral analysis of mesoscale eddies. Part II. Nonlinear analysis. J. Phys. Oceanogr. 43, 2528–2544.Google Scholar
Birner, T., Thompson, J. W. D. & Shepherd, T. G. 2013 Up-gradient eddy fluxes of potential vorticity near the subtropical jet. Geophys. Res. Lett. 40, 5988–5993.Google Scholar
Danabasoglu, G., McWilliams, J. C. & Gent, P. R. 1994 The role of mesoscale tracer transports in the global ocean circulation. Science 264, 1123–1126.Google Scholar
Davey, M. K. & Killworth, P. D. 1984 Isolated waves and eddies in a shallow water model. J. Phys. Oceanogr. 14, 1047–1064.Google Scholar
Eden, C. 2010 Parameterising meso-scale eddy momentum fluxes based on potential vorticity mixing and a gauge term. Ocean Model. 32, 58–71.Google Scholar
Eden, C. 2011 A closure for meso-scale eddy fluxes based on linear instability theory. Ocean Model. 39, 362–369.Google Scholar
Eden, C. & Greatbatch, R. 2007 A diagnosis of thickness fluxes in an eddy-resolving model. J. Phys. Oceanogr. 37, 727–742.Google Scholar
Gent, P. 2011 The Gent–McWilliams parameterization: 20/20 hindsight. Ocean Model. 39, 2–9.Google Scholar
Gent, P. & McWilliams, J. C. 1990 Isopycnal mixing in ocean circulation models. J. Phys. Oceanogr. 20, 150–155.Google Scholar
Haidvogel, D. & Rhines, P. 1983 Waves and circulation driven by oscillatory winds in an idealized ocean basin. Geophys. Astrophys. Fluid Dyn. 25, 1–63.Google Scholar
Hallberg, R. & Gnanadesikan, A. 2006 The role of eddies in determining the structure and response of the wind-driven southern hemisphere overturning: results from the modeling eddies in the Southern Ocean (MESO) project. J. Phys. Oceanogr. 36, 2232–2252.Google Scholar
Iselin, C. O. 1939 The influence of vertical and lateral turbulence on the characteristics of the waters at mid-depths. EOS Trans. AGU 20, 414–417.Google Scholar
Ivchenko, V., Sinha, B., Zalesny, V., Marsh, R. & Blaker, A. 2013 Influence of bottom topography on integral constraints in zonal flows with parameterized potential vorticity fluxes. J. Phys. Oceanogr. 43, 922–943.Google Scholar
Killworth, P. 1997 On the parameterization of eddy transfer. Part I. Theory. J. Mar. Res. 55, 1171–1197.Google Scholar
Li, H. & von Storch, J.-S. 2013 On the fluctuating buoyancy fluxes simulated in a 1/10-degree OGCM. J. Phys. Oceanogr. 43, 1270–1287.Google Scholar
Marshall, D. P., Maddison, J. R. & Berloff, P. 2012 A framework for parameterizing eddy potential vorticity fluxes. J. Phys. Oceanogr. 42, 539–557.Google Scholar
Montgomery, R. B. 1940 The present evidence on the importance of lateral mixing processes in the ocean. Bull. Am. Meteorol. Soc. 21, 87–94.Google Scholar
O’Rourke, A. K. & Vallis, G. K. 2013 Jet interaction and the influence of a minimum phase speed bound on the propagation of eddies. J. Atmos. Sci. 70, 2614–2628.Google Scholar
O’Rourke, A. K. & Vallis, G. K. 2016 Meridional Rossby wave generation and propagation in the maintenance of the wintertime tropospheric double jet. J. Atmos. Sci. 73, 2179–2201.Google Scholar
Porta Mana, P. & Zanna, L. 2014 Toward a stochastic parameterization of ocean mesoscale eddies. Ocean Model. 79, 1–20.Google Scholar
Rypina, I., Kamenkovich, I., Berloff, P. & Pratt, L. 2012 Eddy-induced particle dispersion in the upper-ocean North Atlantic. J. Phys. Oceanogr. 42, 2206–2228.Google Scholar
Speich, S., Dijkstra, H. & Ghil, M. 1995 Successive bifurcations in a shallow-water model applied to the wind-driven ocean circulation. Nonlinear Process. Geophys. 2, 241–268.Google Scholar
Starr, V. 1968 Physics of Negative Viscosity Phenomena, p. 256. McGraw-Hill.Google Scholar
Vallis, G. 2017 Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation, p. 109. Cambridge University Press.Google Scholar
Wardle, R. & Marshall, J. 2000 Representation of eddies in primitive equation models by a PV flux. J. Phys. Oceanogr. 30, 2481–2503.Google Scholar
Waterman, S. & Jayne, S. 2012 Eddy-driven recirculations from a localized transient forcing. J. Phys. Oceanogr. 42, 430–447.Google Scholar