Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tang, G.
Cheng, L.
Lu, L.
Zhao, M.
Tong, F.
and
Dong, G.
2016.
Fluid-Structure-Sound Interactions and Control.
p.
429.
Zhao, Ming
Kaja, Kalyani
Xiang, Yang
and
Cheng, Liang
2016.
Vortex-induced vibration of four cylinders in an in-line square configuration.
Physics of Fluids,
Vol. 28,
Issue. 2,
Tong, Feifei
Cheng, Liang
Xiong, Chengwang
Draper, Scott
An, Hongwei
and
Lou, Xiaofan
2017.
Flow regimes for a square cross-section cylinder in oscillatory flow.
Journal of Fluid Mechanics,
Vol. 813,
Issue. ,
p.
85.
Alam, Md. Mahbub
Zheng, Qinmin
and
Hourigan, Kerry
2017.
The wake and thrust by four side-by-side cylinders at a low Re.
Journal of Fluids and Structures,
Vol. 70,
Issue. ,
p.
131.
Yang, Wanli
Li, Qiao
and
Yeh, Harry
2017.
Calculation Method of Hydrodynamic Forces on Circular Piers during Earthquakes.
Journal of Bridge Engineering,
Vol. 22,
Issue. 11,
Zheng, Qinmin
and
Alam, Md. Mahbub
2017.
Intrinsic features of flow past three square prisms in side-by-side arrangement.
Journal of Fluid Mechanics,
Vol. 826,
Issue. ,
p.
996.
Bhalla, Neelesh
and
Dhiman, Amit Kumar
2017.
Pulsating flow and heat transfer analysis around a heated semi-circular cylinder at low and moderate Reynolds numbers.
Journal of the Brazilian Society of Mechanical Sciences and Engineering,
Vol. 39,
Issue. 8,
p.
3019.
Tang, Guoqiang
Cheng, Liang
Tong, Feifei
Lu, Lin
and
Zhao, Ming
2017.
Modes of synchronisation in the wake of a streamwise oscillatory cylinder.
Journal of Fluid Mechanics,
Vol. 832,
Issue. ,
p.
146.
Tan, Peisen
and
Fan, Dixia
2018.
Numerical simulation of dual oscillating cylinders under different angles for ocean engineering.
p.
1.
Xiong, Chengwang
Cheng, Liang
Tong, Feifei
and
An, Hongwei
2018.
Oscillatory flow regimes for a circular cylinder near a plane boundary.
Journal of Fluid Mechanics,
Vol. 844,
Issue. ,
p.
127.
Xiong, Chengwang
Cheng, Liang
Tong, Feifei
and
An, Hongwei
2018.
On regime C flow around an oscillating circular cylinder.
Journal of Fluid Mechanics,
Vol. 849,
Issue. ,
p.
968.
Munir, Adnan
Zhao, Ming
Wu, Helen
and
Lu, Lin
2019.
Effects of gap ratio on flow-induced vibration of two rigidly coupled side-by-side cylinders.
Journal of Fluids and Structures,
Vol. 91,
Issue. ,
p.
102726.
Ren, Chengjiao
Cheng, Liang
Tong, Feifei
Xiong, Chengwang
and
Chen, Tingguo
2019.
Oscillatory flow regimes around four cylinders in a diamond arrangement.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
p.
955.
Pearcey, T.
Zhao, M.
and
Xiang, Y.
2019.
Fluid-Structure-Sound Interactions and Control.
p.
235.
Etminan, Vahid
Lowe, Ryan J.
and
Ghisalberti, Marco
2019.
Canopy resistance on oscillatory flows.
Coastal Engineering,
Vol. 152,
Issue. ,
p.
103502.
Zhao, Ming
2020.
Flow induced by an oscillating circular cylinder close to a plane boundary in quiescent fluid.
Journal of Fluid Mechanics,
Vol. 897,
Issue. ,
Wu, Bo
Li, Shaopeng
Cao, Shuyang
Yang, Qingshan
and
Zhang, Liangliang
2020.
Numerical investigation of the separated and reattaching flow over a 5:1 rectangular cylinder in streamwise sinusoidal flow.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 198,
Issue. ,
p.
104120.
Haibullina, A I
Hayrullin, A R
Ilyin, V K
and
Savelyeva, A D
2020.
Improving the thermal efficiency in heat exchangers of transport vehicles.
IOP Conference Series: Materials Science and Engineering,
Vol. 918,
Issue. 1,
p.
012162.
Kumar, Rajesh
and
Singh, Nirmal Kant
2020.
Large eddy simulation of flow over square cylinder arrays in an octagonal configuration at subcritical Reynolds numbers.
Heat Transfer,
Vol. 49,
Issue. 6,
p.
3267.
Ahmad, Shafee
Ul-Islam, Shams
and
Zeeshan, Ahmed
2021.
Numerical Investigation of Fluid Flow past Four Cylinders at Low Reynolds Numbers.
Mathematical Problems in Engineering,
Vol. 2021,
Issue. ,
p.
1.
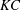 $\mathit{KC}$ and
$\mathit{KC}$ and 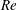 $\mathit{Re}$ conditions
$\mathit{Re}$ conditions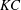 $\mathit{KC}$) ranging from 1 to 12 and at Reynolds numbers (
$\mathit{KC}$) ranging from 1 to 12 and at Reynolds numbers (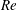 $\mathit{Re}$) from 20 to 200. A set of flow patterns is observed and classified based on known oscillatory flow regimes around a single cylinder. These include six types of reflection symmetry regimes to the axis of flow oscillation, two types of spatio-temporal symmetry regimes and a series of symmetry-breaking flow patterns. In general, at small gap distances, the four structures behave more like a single body, and the flow fields therefore resemble those around a single cylinder with a large effective cylinder diameter. With increasing gap distance, flow structures around each individual cylinder in the array start to influence the overall flow patterns, and the flow field shows a variety of symmetry and asymmetry patterns as a result of vortex and shear layer interactions. The characteristics of hydrodynamic forces on individual cylinders as well as on the cylinder group are also examined. It is found that the hydrodynamic forces respond in a similar manner to the flow field to the cylinder proximity and wake interference.
$\mathit{Re}$) from 20 to 200. A set of flow patterns is observed and classified based on known oscillatory flow regimes around a single cylinder. These include six types of reflection symmetry regimes to the axis of flow oscillation, two types of spatio-temporal symmetry regimes and a series of symmetry-breaking flow patterns. In general, at small gap distances, the four structures behave more like a single body, and the flow fields therefore resemble those around a single cylinder with a large effective cylinder diameter. With increasing gap distance, flow structures around each individual cylinder in the array start to influence the overall flow patterns, and the flow field shows a variety of symmetry and asymmetry patterns as a result of vortex and shear layer interactions. The characteristics of hydrodynamic forces on individual cylinders as well as on the cylinder group are also examined. It is found that the hydrodynamic forces respond in a similar manner to the flow field to the cylinder proximity and wake interference.


