Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Budanur, Nazmi Burak
Dogra, Akshunna Shaurya
and
Hof, Björn
2019.
Geometry of transient chaos in streamwise-localized pipe flow turbulence.
Physical Review Fluids,
Vol. 4,
Issue. 10,
Doohan, Patrick
Willis, Ashley P.
and
Hwang, Yongyun
2019.
Shear stress-driven flow: the state space of near-wall turbulence as .
Journal of Fluid Mechanics,
Vol. 874,
Issue. ,
p.
606.
Keeler, Jack S.
Thompson, Alice B.
Lemoult, Grégoire
Juel, Anne
and
Hazel, Andrew L.
2019.
The influence of invariant solutions on the transient behaviour of an air bubble in a Hele-Shaw channel.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 475,
Issue. 2232,
p.
20190434.
Deguchi, Kengo
2019.
High-speed shear-driven dynamos. Part 2. Numerical analysis.
Journal of Fluid Mechanics,
Vol. 876,
Issue. ,
p.
830.
Ahmed, M. Arslan
and
Sharma, Ati S.
2020.
Basis for finding exact coherent states.
Physical Review E,
Vol. 101,
Issue. 1,
Davis, Ethan A.
and
Park, Jae Sung
2020.
Dynamics of laminar and transitional flows over slip surfaces: effects on the laminar–turbulent separatrix.
Journal of Fluid Mechanics,
Vol. 894,
Issue. ,
Graham, Michael D.
and
Floryan, Daniel
2021.
Exact Coherent States and the Nonlinear Dynamics of Wall-Bounded Turbulent Flows.
Annual Review of Fluid Mechanics,
Vol. 53,
Issue. 1,
p.
227.
Sasaki, Eiichi
Kawahara, Genta
and
Jiménez, Javier
2021.
Bifurcation structure of unstable periodic orbits in plane Couette flow with the Smagorinsky model.
Physical Review Fluids,
Vol. 6,
Issue. 8,
Lellep, Martin
Prexl, Jonathan
Eckhardt, Bruno
and
Linkmann, Moritz
2022.
Interpreted machine learning in fluid dynamics: explaining relaminarisation events in wall-bounded shear flows.
Journal of Fluid Mechanics,
Vol. 942,
Issue. ,
Pershin, Anton
Beaume, Cédric
Eaves, Tom S.
and
Tobias, Steven M.
2022.
Optimizing the control of transition to turbulence using a Bayesian method.
Journal of Fluid Mechanics,
Vol. 941,
Issue. ,
Wang, B.
Ayats, R.
Deguchi, K.
Mellibovsky, F.
and
Meseguer, A.
2022.
Self-sustainment of coherent structures in counter-rotating Taylor–Couette flow.
Journal of Fluid Mechanics,
Vol. 951,
Issue. ,
Lawless, Jack
Keeler, Jack
Gaillard, Antoine
Hazel, Andrew
and
Juel, Anne
2022.
The unpredictable nature of bubble evolution.
Scientific Reports,
Vol. 12,
Issue. 1,
Bengana, Yacine
Yang, Qiang
Tu, Guohua
and
Hwang, Yongyun
2022.
Exact coherent states in plane Couette flow under spanwise wall oscillation.
Journal of Fluid Mechanics,
Vol. 947,
Issue. ,
Avila, Marc
Barkley, Dwight
and
Hof, Björn
2023.
Transition to Turbulence in Pipe Flow.
Annual Review of Fluid Mechanics,
Vol. 55,
Issue. 1,
p.
575.
Paranjape, Chaitanya S.
Yalnız, Gökhan
Duguet, Yohann
Budanur, Nazmi Burak
and
Hof, Björn
2023.
Direct Path from Turbulence to Time-Periodic Solutions.
Physical Review Letters,
Vol. 131,
Issue. 3,
Lustro, Julius Rhoan T.
Shimizu, Yudai
and
Kawahara, Genta
2023.
Homoclinic bifurcation and switching of edge state in plane Couette flow.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 33,
Issue. 6,
Feldmann, Daniel
Borrero-Echeverry, Daniel
Burin, Michael J.
Avila, Kerstin
and
Avila, Marc
2023.
Routes to turbulence in Taylor–Couette flow.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 381,
Issue. 2246,
Sano, Alex
Cavalieri, André V.G.
da Silva, André F.C.
and
Wolf, William R.
2023.
On the emergence of secondary tones in airfoil noise.
Journal of Fluid Mechanics,
Vol. 966,
Issue. ,
McCormack, Matthew
Cavalieri, André V.G.
and
Hwang, Yongyun
2024.
Multi-scale invariant solutions in plane Couette flow: a reduced-order model approach.
Journal of Fluid Mechanics,
Vol. 983,
Issue. ,
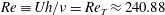 $Re\equiv Uh/\unicode[STIX]{x1D708}=Re_{T}\approx 240.88$ (
$Re\equiv Uh/\unicode[STIX]{x1D708}=Re_{T}\approx 240.88$ (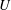 $U$,
$U$, 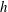 $h$, and
$h$, and  $\unicode[STIX]{x1D708}$ being half the difference of the two wall velocities, half the wall separation, and the kinematic viscosity of fluid, respectively). At
$\unicode[STIX]{x1D708}$ being half the difference of the two wall velocities, half the wall separation, and the kinematic viscosity of fluid, respectively). At 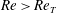 $Re>Re_{T}$ a Smale horseshoe appears on the Poincaré section through transversal homoclinic points to generate a transient chaos that eventually relaminarises. In numerical experiments a sustaining chaos, which is a consequence of period-doubling cascade stemming from the upper branch of another saddle-node pair of periodic orbits, is observed in a narrow range of the Reynolds number,
$Re>Re_{T}$ a Smale horseshoe appears on the Poincaré section through transversal homoclinic points to generate a transient chaos that eventually relaminarises. In numerical experiments a sustaining chaos, which is a consequence of period-doubling cascade stemming from the upper branch of another saddle-node pair of periodic orbits, is observed in a narrow range of the Reynolds number, 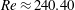 $Re\approx 240.40$–240.46. At the upper edge of this
$Re\approx 240.40$–240.46. At the upper edge of this 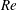 $Re$ range it is found that the chaotic set touches the lower branch of this pair, i.e., another edge state. The corresponding chaotic attractor is replaced by a chaotic saddle at
$Re$ range it is found that the chaotic set touches the lower branch of this pair, i.e., another edge state. The corresponding chaotic attractor is replaced by a chaotic saddle at 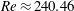 $Re\approx 240.46$, and subsequently this saddle touches the gentle periodic edge state on the boundary of the laminar basin at the tangency Reynolds number
$Re\approx 240.46$, and subsequently this saddle touches the gentle periodic edge state on the boundary of the laminar basin at the tangency Reynolds number 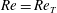 $Re=Re_{T}$. After this crisis on the boundary of the laminar basin, for
$Re=Re_{T}$. After this crisis on the boundary of the laminar basin, for 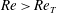 $Re>Re_{T}$, chaotic transients that eventually relaminarise can be observed.
$Re>Re_{T}$, chaotic transients that eventually relaminarise can be observed.

