A Boussinesq fluid of kinematic velocity and thermal diffusivity is confined within a rapidly rotating shell with inner and outer sphere boundary radii 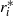and 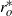, respectively. The boundaries of the shell corotate at angular velocity 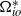and a continuously varying stratification profile is applied which is unstable in 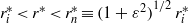and stable in 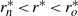. When 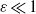, the unstable zone attached to the inner boundary is thin. As in previous small Ekman number 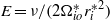studies, convection at the onset of instability takes on the familiar ‘cartridge belt’ structure, which is localized within a narrow layer adjacent to, but outside, the cylinder tangent to the inner sphere at its equator (Dormy et al. J. Fluid Mech., 2004, vol. 501, pp. 43–70), with estimated radial width of order 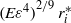. The azimuthally propagating convective columns, described by the cartridge belt, reside entirely within the unstable layer when , and extend from the equatorial plane an axial distance 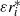along the tangent cylinder as far as its intersection with the neutrally stable spherical surface 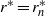. We investigate the eigensolutions of the ordinary differential equation governing the axial structure of the cartridge belt both numerically for moderate-to-small values of the stratification parameter and analytically when 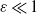. At the lowest order of the expansion in powers of , the eigenmodes resemble those for classical plane layer convection, being either steady (exchange of stabilities) or, for small Prandtl number 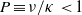, oscillatory (overstability) with a frequency 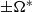. At the next order, the axial variation of the basic state removes any plane layer degeneracies. First, the exchange of stabilities modes oscillate at a low frequency causing the short axial columns to propagate as a wave with a small angular velocity, termed slow modes. Second, the magnitudes of both the Rayleigh number and frequency of the two overstable modes, termed fast modes, split. When 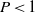the slow modes that exist at large azimuthal wavenumbers 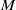make a continuous transition to the preferred fast modes at small 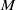. At all values of 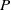the critical Rayleigh number corresponds to a mode exhibiting prograde propagation, whether it be a fast or slow mode. This feature is shared by the uniform classical convective shell models, as well as Busse’s celebrated annulus model. None of them possess any stable stratification and typically are prone to easily excitable Rossby or inertial modes of convection at small 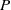. By way of contrast these structures cannot exist in our model for small due to the viscous damping in the outer thick stable region.