Article contents
Onset of fully compressible convection in a rapidly rotating spherical shell
Published online by Cambridge University Press: 01 July 2019
Abstract
The onset of thermal convection in a rapidly rotating spherical shell is studied by linear stability analysis based on the fully compressible Navier–Stokes equations. Compressibility is quantified by the number of density scale heights 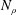 $N_{\unicode[STIX]{x1D70C}}$, which measures the intensity of density stratification of the motionless, polytropic base state. The nearly adiabatic flow with polytropic index
$N_{\unicode[STIX]{x1D70C}}$, which measures the intensity of density stratification of the motionless, polytropic base state. The nearly adiabatic flow with polytropic index 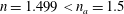 $n=1.499<n_{a}=1.5$ is considered, where
$n=1.499<n_{a}=1.5$ is considered, where 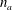 $n_{a}$ is the adiabatic polytropic index. By investigating the stability of the base state with respect to the disturbance of specified wavenumber, the instability process is found to be sensitive to the Prandtl number
$n_{a}$ is the adiabatic polytropic index. By investigating the stability of the base state with respect to the disturbance of specified wavenumber, the instability process is found to be sensitive to the Prandtl number 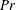 $Pr$ and to
$Pr$ and to 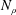 $N_{\unicode[STIX]{x1D70C}}$. For large
$N_{\unicode[STIX]{x1D70C}}$. For large 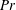 $Pr$ and small
$Pr$ and small 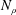 $N_{\unicode[STIX]{x1D70C}}$, the quasi-geostrophic columnar mode loses stability first; while for relatively small
$N_{\unicode[STIX]{x1D70C}}$, the quasi-geostrophic columnar mode loses stability first; while for relatively small  $Pr$ a new quasi-geostrophic compressible mode is identified, which becomes unstable first under strong density stratification. The inertial mode can also occur first for relatively small
$Pr$ a new quasi-geostrophic compressible mode is identified, which becomes unstable first under strong density stratification. The inertial mode can also occur first for relatively small  $Pr$ and a certain intensity of density stratification in the parameter range considered. Although the Rayleigh numbers
$Pr$ and a certain intensity of density stratification in the parameter range considered. Although the Rayleigh numbers 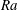 $Ra$ for the onsets of the quasi-geostrophic compressible mode and columnar mode are different by several orders of magnitude, we find that they follow very similar scaling laws with the Taylor number. The critical
$Ra$ for the onsets of the quasi-geostrophic compressible mode and columnar mode are different by several orders of magnitude, we find that they follow very similar scaling laws with the Taylor number. The critical 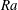 $Ra$ for convection onset is found to be always positive, in contrast with previous results based on the widely used anelastic model that convection can occur at negative
$Ra$ for convection onset is found to be always positive, in contrast with previous results based on the widely used anelastic model that convection can occur at negative 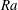 $Ra$. By evaluating the relative magnitude of the time derivative of density perturbation in the continuity equation, we show that the anelastic approximation in the present system cannot be applied in the small-
$Ra$. By evaluating the relative magnitude of the time derivative of density perturbation in the continuity equation, we show that the anelastic approximation in the present system cannot be applied in the small- $Ra$ and large-
$Ra$ and large-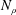 $N_{\unicode[STIX]{x1D70C}}$ regime.
$N_{\unicode[STIX]{x1D70C}}$ regime.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 11
- Cited by



