Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jonker, Harmen J. J.
and
Jiménez, Maria A.
2014.
Laboratory Experiments on Convective Entrainment Using a Saline Water Tank.
Boundary-Layer Meteorology,
Vol. 151,
Issue. 3,
p.
479.
Perrin, Vincent E.
and
Jonker, Harmen J. J.
2015.
Lagrangian Droplet Dynamics in the Subsiding Shell of a Cloud Using Direct Numerical Simulations.
Journal of the Atmospheric Sciences,
Vol. 72,
Issue. 10,
p.
4015.
Waggy, Scott B.
Biringen, Sedat
and
Kucala, Alec
2015.
Wake effects on turbulent transport in the convective boundary layer.
Geophysical & Astrophysical Fluid Dynamics,
Vol. 109,
Issue. 5,
p.
465.
Tomas, J.M.
Pourquie, M.J.B.M.
and
Jonker, H.J.J.
2015.
The influence of an obstacle on flow and pollutant dispersion in neutral and stable boundary layers.
Atmospheric Environment,
Vol. 113,
Issue. ,
p.
236.
Schalkwijk, Jerôme
Jonker, Harmen J. J.
Siebesma, A. Pier
and
Van Meijgaard, Erik
2015.
Weather Forecasting Using GPU-Based Large-Eddy Simulations.
Bulletin of the American Meteorological Society,
Vol. 96,
Issue. 5,
p.
715.
Sullivan, Peter P.
Weil, Jeffrey C.
Patton, Edward G.
Jonker, Harmen J. J.
and
Mironov, Dmitrii V.
2016.
Turbulent Winds and Temperature Fronts in Large-Eddy Simulations of the Stable Atmospheric Boundary Layer.
Journal of the Atmospheric Sciences,
Vol. 73,
Issue. 4,
p.
1815.
Kozul, M.
Chung, D.
and
Monty, J. P.
2016.
Direct numerical simulation of the incompressible temporally developing turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 796,
Issue. ,
p.
437.
Mukherjee, Siddhartha
Schalkwijk, Jerôme
and
Jonker, Harmen J. J.
2016.
Predictability of Dry Convective Boundary Layers: An LES Study.
Journal of the Atmospheric Sciences,
Vol. 73,
Issue. 7,
p.
2715.
Liu, Peng
Sun, Jianning
and
Shen, Lidu
2016.
Parameterization of sheared entrainment in a well-developed CBL. Part II: A simple model for predicting the growth rate of the CBL.
Advances in Atmospheric Sciences,
Vol. 33,
Issue. 10,
p.
1185.
Tomas, J. M.
Pourquie, M. J. B. M.
and
Jonker, H. J. J.
2016.
Stable Stratification Effects on Flow and Pollutant Dispersion in Boundary Layers Entering a Generic Urban Environment.
Boundary-Layer Meteorology,
Vol. 159,
Issue. 2,
p.
221.
Cristini, A.
Meakin, C.
Hirschi, R.
Arnett, D.
Georgy, C.
Viallet, M.
and
Walkington, I.
2017.
3D hydrodynamic simulations of carbon burning in massive stars.
Monthly Notices of the Royal Astronomical Society,
Vol. 471,
Issue. 1,
p.
279.
Tomas, J. M.
Eisma, H. E.
Pourquie, M. J. B. M.
Elsinga, G. E.
Jonker, H. J. J.
and
Westerweel, J.
2017.
Pollutant Dispersion in Boundary Layers Exposed to Rural-to-Urban Transitions: Varying the Spanwise Length Scale of the Roughness.
Boundary-Layer Meteorology,
Vol. 163,
Issue. 2,
p.
225.
Mellado, Juan Pedro
Puche, Marc
and
van Heerwaarden, Chiel C.
2017.
Moisture statistics in free convective boundary layers growing into linearly stratified atmospheres.
Quarterly Journal of the Royal Meteorological Society,
Vol. 143,
Issue. 707,
p.
2403.
Pham, H. T.
and
Sarkar, S.
2017.
Turbulent entrainment in a strongly stratified barrier layer.
Journal of Geophysical Research: Oceans,
Vol. 122,
Issue. 6,
p.
5075.
Pratt, J.
Baraffe, I.
Goffrey, T.
Constantino, T.
Viallet, M.
Popov, M. V.
Walder, R.
and
Folini, D.
2017.
Extreme value statistics for two-dimensional convective penetration in a pre-main sequence star.
Astronomy & Astrophysics,
Vol. 604,
Issue. ,
p.
A125.
Fedorovich, Evgeni
Gibbs, Jeremy A.
and
Shapiro, Alan
2017.
Numerical Study of Nocturnal Low-Level Jets over Gently Sloping Terrain.
Journal of the Atmospheric Sciences,
Vol. 74,
Issue. 9,
p.
2813.
Heller, Valentin
2017.
Self-similarity and Reynolds number invariance in Froude modelling.
Journal of Hydraulic Research,
Vol. 55,
Issue. 3,
p.
293.
van Reeuwijk, Maarten
and
Jonker, Harm J. J.
2018.
Direct and Large-Eddy Simulation X.
Vol. 24,
Issue. ,
p.
53.
Cristini, A
Hirschi, R
Meakin, C
Arnett, D
Georgy, C
and
Walkington, I
2019.
Dependence of convective boundary mixing on boundary properties and turbulence strength.
Monthly Notices of the Royal Astronomical Society,
Vol. 484,
Issue. 4,
p.
4645.
LeMone, Margaret A.
Angevine, Wayne M.
Bretherton, Christopher S.
Chen, Fei
Dudhia, Jimy
Fedorovich, Evgeni
Katsaros, Kristina B.
Lenschow, Donald H.
Mahrt, Larry
Patton, Edward G.
Sun, Jielun
Tjernström, Michael
and
Weil, Jeffrey
2019.
100 Years of Progress in Boundary Layer Meteorology.
Meteorological Monographs,
Vol. 59,
Issue. ,
p.
9.1.
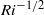 $R{i}^{- 1/ 2} $. In addition, it is observed that all cases evolve in a self-similar fashion. A self-similarity analysis of the conservation equations shows that only a square root growth law is consistent with self-similar behaviour.
$R{i}^{- 1/ 2} $. In addition, it is observed that all cases evolve in a self-similar fashion. A self-similarity analysis of the conservation equations shows that only a square root growth law is consistent with self-similar behaviour.

