Article contents
On the scaling of propagation of periodically generated vortex rings
Published online by Cambridge University Press: 22 August 2018
Abstract
The propagation of periodically generated vortex rings (period 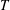 $T$) is numerically investigated by imposing pulsed jets of velocity
$T$) is numerically investigated by imposing pulsed jets of velocity  $U_{jet}$ and duration
$U_{jet}$ and duration 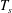 $T_{s}$ (no flow between pulses) at the inlet of a cylinder of diameter
$T_{s}$ (no flow between pulses) at the inlet of a cylinder of diameter 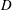 $D$ exiting into a tank. Because of the step-like nature of pulsed jet waveforms, the average jet velocity during a cycle is
$D$ exiting into a tank. Because of the step-like nature of pulsed jet waveforms, the average jet velocity during a cycle is 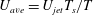 $U_{ave}=U_{jet}T_{s}/T$. By using
$U_{ave}=U_{jet}T_{s}/T$. By using 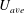 $U_{ave}$ in the definition of the Reynolds number (
$U_{ave}$ in the definition of the Reynolds number (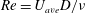 $Re=U_{ave}D/\unicode[STIX]{x1D708}$,
$Re=U_{ave}D/\unicode[STIX]{x1D708}$,  $\unicode[STIX]{x1D708}$: kinematic viscosity of fluid) and non-dimensional period (
$\unicode[STIX]{x1D708}$: kinematic viscosity of fluid) and non-dimensional period (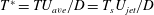 $T^{\ast }=TU_{ave}/D=T_{s}U_{jet}/D$, i.e. equivalent to formation time), then based on the results, the vortex ring velocity
$T^{\ast }=TU_{ave}/D=T_{s}U_{jet}/D$, i.e. equivalent to formation time), then based on the results, the vortex ring velocity 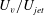 $U_{v}/U_{jet}$ becomes approximately independent of the stroke ratio
$U_{v}/U_{jet}$ becomes approximately independent of the stroke ratio 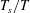 $T_{s}/T$. The results also show that
$T_{s}/T$. The results also show that 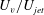 $U_{v}/U_{jet}$ increases by reducing
$U_{v}/U_{jet}$ increases by reducing 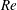 $Re$ or increasing
$Re$ or increasing 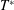 $T^{\ast }$ (more sensitive to
$T^{\ast }$ (more sensitive to 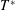 $T^{\ast }$) according to a power law of the form
$T^{\ast }$) according to a power law of the form 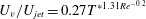 $U_{v}/U_{jet}=0.27T^{\ast 1.31Re^{-0.2}}$. An empirical relation, therefore, for the location of vortex ring core centres (
$U_{v}/U_{jet}=0.27T^{\ast 1.31Re^{-0.2}}$. An empirical relation, therefore, for the location of vortex ring core centres (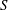 $S$) over time (
$S$) over time ( $t$) is proposed (
$t$) is proposed (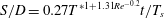 $S/D=0.27T^{\ast 1+1.31Re^{-0.2}}t/T_{s}$), which collapses (scales) not only our results but also the results of experiments for non-periodic rings. This might be due to the fact that the quasi-steady vortex ring velocity was found to have a maximum of 15 % difference with the initial (isolated) one. Visualizing the rings during the periodic state shows that at low
$S/D=0.27T^{\ast 1+1.31Re^{-0.2}}t/T_{s}$), which collapses (scales) not only our results but also the results of experiments for non-periodic rings. This might be due to the fact that the quasi-steady vortex ring velocity was found to have a maximum of 15 % difference with the initial (isolated) one. Visualizing the rings during the periodic state shows that at low 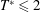 $T^{\ast }\leqslant 2$ and high
$T^{\ast }\leqslant 2$ and high 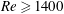 $Re\geqslant 1400$ here, the stopping vortices become unstable and form hairpin vortices around the leading ones. However, by increasing
$Re\geqslant 1400$ here, the stopping vortices become unstable and form hairpin vortices around the leading ones. However, by increasing 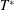 $T^{\ast }$ or decreasing
$T^{\ast }$ or decreasing 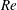 $Re$ the stopping vortices remain circular. Furthermore, rings with short
$Re$ the stopping vortices remain circular. Furthermore, rings with short 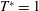 $T^{\ast }=1$ show vortex pairing after approximately one period in the downstream, but higher
$T^{\ast }=1$ show vortex pairing after approximately one period in the downstream, but higher 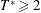 $T^{\ast }\geqslant 2$ generates a train of vortices in the quasi-steady state.
$T^{\ast }\geqslant 2$ generates a train of vortices in the quasi-steady state.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
Asadi et al. supplementary movie 1
The isosurface of vorticity magnitude colored by helicity starting from rest (t=0) to quasi-steady state for case 3 (Re=1400, T*=1). Link in the text: Movie 1
Asadi et al. supplementary movie 2
Out-of-plane vorticity for case 3 (Re=1400, T*=1) contours starting from rest (t=0) to quasi-steady state. Link in the text: Movie 2
Asadi et al. supplementary movie 3
Out-of-plane vorticity on the midplane for case 3 (Re=1400, T*=1) contours during quasi-steady state. Link in the text: Movie 3
Asadi et al. supplementary movie 4
Out-of-plane vorticity on the midplane for case 4 (Re=1400, T*=2) contours during quasi-steady state. Link in the text: Movie 4
Asadi et al. supplementary movie 5
Out-of-plane vorticity on the midplane for case 5 (Re=11,500, T*=1) contours during quasi-steady state. Link in the text: Movie 5
Asadi et al. supplementary movie 6
Out-of-plane vorticity on the midplane for case 6 (Re=11,500, T*=2) contours during quasi-steady state. Link in the text: Movie 6
- 28
- Cited by


