Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-22T02:18:09.022Z Has data issue: false hasContentIssue false
  • English
  • Français

On the dynamics of vortex–droplet interactions, dispersion and breakup in a coaxial swirling flow

Published online by Cambridge University Press:  30 August 2017

Kuppuraj Rajamanickam  and
Saptarshi Basu Open the ORCID record for Saptarshi Basu [Opens in a new window]
Kuppuraj Rajamanickam
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore-560012, India
Saptarshi Basu*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore-560012, India
*
†Email address for correspondence: sbasu@mecheng.iisc.ernet.in
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper discusses the fundamental mechanisms of vortex–droplet interactions leading to flow distortion, droplet dispersion and breakup in a complex swirling gas flow field. In particular, the way in which the location of droplet injection determines the degree of inhomogeneous dispersion and breakup modes has been elucidated in detail using high-fidelity laser diagnostics. The droplets are injected as monodispersed streams at various spatial locations such as the vortex breakdown bubble and the shear layers (inner and outer) exhibited by the swirling flow. Simultaneous time-resolved particle image velocimetry ($3500~\text{frames}~\text{s}^{-1}$) and high-speed shadowgraphy measurements are employed to delineate the two-phase interaction dynamics. These measurements have been used to evaluate the fluctuations in instantaneous circulation strength 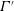$\unicode[STIX]{x1D6E4}^{\prime }$ caused by the flow field eddies and the resultant angular dispersion in the droplet trajectories 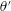$\unicode[STIX]{x1D703}^{\prime }$. The droplet–flow interactions show two-way coupling at low momentum ratios (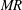$MR$) and strong one-way coupling at high momentum ratios. The gas phase flow field is globally altered at low airflow rates (low 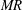$MR$) due to impact of droplets with the vortex core. The flow perturbation is found to be minimal and mainly local at high airflow rates (high 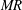$MR$). Spectral coherence analysis is carried out to understand the correlation between eddy circulation strength 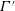$\unicode[STIX]{x1D6E4}^{\prime }$ and droplet dispersion 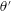$\unicode[STIX]{x1D703}^{\prime }$. The droplet dispersion shows strong coherence with the flow in certain frequency bands. Subsequently, proper orthogonal decomposition (POD) is implemented to elucidate the governing instability mechanism and frequency signatures associated with the turbulent coherent structures. The POD results suggest dominance of the Kelvin–Helmholtz (KH) instability mode (axial and azimuthal shear). The frequency range pertaining to high coherence between dispersion and circulation shows good agreement with KH instability quantified from POD analysis. The droplets injected at the inner shear layer (ISL) and outer shear layer (OSL) show different interaction dynamics. For instance, droplet dispersion at the OSL exhibits secondary frequency (shedding mode) coupling in addition to the KH mode, whereas ISL injection couples only in a single narrow frequency band (i.e. KH mode). Further, high-speed shadow imaging (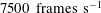$7500~\text{frames}~\text{s}^{-1}$) is employed to visualize the breakup dynamics of the droplets. The effect of coherent structures on the droplet breakup modes is shown as a function of the Weber number (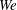$We$) defined based on the circulation strength. The wide fluctuations caused in the instantaneous circulation strength lead to different breakup modes (bag, multimodal, shear thinning, catastrophic) even for fixed airflow rates. These fluctuations also lead to inhomogeneous spatial dispersion of the droplets in the swirling gas flow field. We are able to present the dispersion contours in terms of the Stokes number and a spatial homogeneity parameter. In essence, the dispersion inhomogeneity is found to be a strong function of the injection location, the phase relationship with the eddies and the momentum ratio (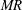$MR$).

JFM classification

Drops and Bubbles: Breakup/coalescence Drops and Bubbles: Drops and Bubbles Vortex Flows: Vortex interactions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 827 , 25 September 2017 , pp. 572 - 613
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 1991 Particle-imaging techniques for experimental fluid mechanics. Annu. Rev. Fluid Mech. 23, 261–304.Google Scholar
Aggarwal, S. K. 1994 Relationship between Stokes number and intrinsic frequencies in particle-laden flows. AIAA J. 32, 1322–1325.Google Scholar
Aggarwal, S. K. & Park, T. W. 1999 Dispersion of evaporating droplets in a swirling axisymmetric jet. AIAA J. 37, 1578–1587.CrossRefGoogle Scholar
Al Taweel, A. M. & Landau, J. 1977 Turbulence modulation in two-phase jets. Intl J. Multiphase Flow 3, 341–351.Google Scholar
Albrecht, H.-E., Damaschke, N., Borys, M. & Tropea, C. 2013 Laser Doppler and Phase Doppler Measurement Techniques. Springer.Google Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.Google Scholar
Beér, J. M. & Chigier, N. A. 1972 Combustion Aerodynamics. Applied Science Publishers Ltd.Google Scholar
Bendat, J. S. & Piersol, A. G. 1980 Engineering Applications of Correlation and Spectral Analysis. Wiley-Interscience.Google Scholar
Benjamin, T. B. 1962 Theory of the vortex breakdown phenomenon. J. Fluid Mech. 14, 593–629.Google Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575.Google Scholar
Billant, P., Chomaz, J.-M. & Huerre, P. 1998 Experimental study of vortex breakdown in swirling jets. J. Fluid Mech. 376, 183–219.Google Scholar
Boileau, M., Pascaud, S., Riber, E., Cuenot, B., Gicquel, L. Y. M., Poinsot, T. J. & Cazalens, M. 2008 Investigation of two-fluid methods for large eddy simulation of spray combustion in gas turbines. Flow Turbul. Combust. 80, 291–321.Google Scholar
Cebeci, T. & Bradshaw, P. 1977 Momentum Transfer in Boundary Layers. McGraw-Hill.Google Scholar
Champagne, F. H. & Kromat, S. 2000 Experiments on the formation of a recirculation zone in swirling coaxial jets. Exp. Fluids 29, 494–504.CrossRefGoogle Scholar
Chandrasekhar, S. 2013 Hydrodynamic and Hydromagnetic Stability. Courier Corporation.Google Scholar
Chigier, N. A. & Chervinsky, A. 1967 Experimental investigation of swirling vortex motion in jets. Trans. ASME J. Appl. Mech. 34, 443–451.Google Scholar
Chou, W.-H., Hsiang, L.-P. & Faeth, G. M. 1997 Temporal properties of drop breakup in the shear breakup regime. Intl J. Multiphase Flow 23, 651–669.Google Scholar
Chung, J. N. & Troutt, T. R. 1988 Simulation of particle dispersion in an axisymmetric jet. J. Fluid Mech. 186, 199–222.CrossRefGoogle Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21, 385–425.Google Scholar
Crowe, C. T., Chung, J. N. & Troutt, T. R. 1988 Particle mixing in free shear flows. Prog. Energy Combust. Sci. 14, 171–194.Google Scholar
Crowe, C. T., Sommerfeld, M. & Tsuji, Y. 1998 Fundamentals of Gas–Particle and Gas–Droplet Flows. CRC.Google Scholar
Crowe, C. T., Troutt, T. R. & Chung, J. N. 1996 Numerical models for two-phase turbulent flows. Annu. Rev. Fluid Mech. 28, 11–43.Google Scholar
Czainski, A., Garncarek, Z. & Piasecki, R. 1994 Quantitative characterization of inhomogeneity in thin metallic films using Garncarek’s method. J. Phys. D: Appl. Phys. 27 (3), 616–622.CrossRefGoogle Scholar
Dai, Z. & Faeth, G. M. 2001 Temporal properties of secondary drop breakup in the multimode breakup regime. Intl J. Multiphase Flow 27, 217–236.Google Scholar
Danon, H., Wolfshtein, M. & Hetsroni, G. 1977 Numerical calculations of two-phase turbulent round jet. Intl J. Multiphase Flow 3, 223–234.Google Scholar
Dimotakis, P. E. 1986 Two-dimensional shear-layer entrainment. AIAA J. 24, 1791–1796.Google Scholar
Elghobashi, S. E. & Abou-Arab, T. W. 1983 A two-equation turbulence model for two-phase flows. Phys. Fluids 26, 931–938.Google Scholar
Elghobashi, S. & Truesdell, G. C. 1993 On the two-way interaction between homogeneous turbulence and dispersed solid particles. I: turbulence modification. Phys. Fluids Fluid Dyn. 5, 1790–1801.Google Scholar
Engelbert, C., Hardalupas, Y. & Whitelaw, J. H. 1995 Breakup phenomena in coaxial airblast atomizers. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, pp. 189–229. The Royal Society.Google Scholar
Faeth, G. M., Hsiang, L.-P. & Wu, P.-K. 1995 Structure and breakup properties of sprays. Intl J. Multiphase Flow 21, 99–127.Google Scholar
Fessler, J. R., Kulick, J. D. & Eaton, J. K. 1994 Preferential concentration of heavy particles in a turbulent channel flow. Phys. Fluids 6, 3742–3749.Google Scholar
Flock, A. K., Guildenbecher, D. R., Chen, J., Sojka, P. E. & Bauer, H.-J. 2012 Experimental statistics of droplet trajectory and air flow during aerodynamic fragmentation of liquid drops. Intl J. Multiphase Flow 47, 37–49.Google Scholar
Gallaire, F. & Chomaz, J.-M. 2003 Instability mechanisms in swirling flows. Phys. Fluids 15, 2622–2639.Google Scholar
Garncarek, Z.1993 Constructions of the measures of distribution features for finite point sets with examples of applications in natural and technical sciences. ZN WSP Opole Stud. Monogr. NR 203, 1–114.Google Scholar
Gillandt, I., Fritsching, U. & Bauckhage, K. 2001 Measurement of phase interaction in dispersed gas/particle two-phase flow. Intl J. Multiphase Flow 27, 1313–1332.Google Scholar
Gu, X., Basu, S. & Kumar, R. 2012 Dispersion and vaporization of biofuels and conventional fuels in a crossflow pre-mixer. Intl J. Heat Mass Transfer 55, 336–346.Google Scholar
Guildenbecher, D. R., López-Rivera, C. & Sojka, P. E. 2009 Secondary atomization. Exp. Fluids 46, 371–402.CrossRefGoogle Scholar
Hall, M. G. 1967 A new approach to vortex breakdown. In 14th Atmospheric Flight Mechanics Conference, pp. 319–340. AIAA Paper 1987-2495.Google Scholar
Han, J. & Tryggvason, G. 1999 Secondary breakup of axisymmetric liquid drops. I. Acceleration by a constant body force. Phys. Fluids 11, 3650–3667.Google Scholar
Hanson, A. R., Domich, E. G. & Adams, H. S. 1963 Shock tube investigation of the breakup of drops by air blasts. Phys. Fluids 6, 1070–1080.Google Scholar
Hayakawa, S., Okajima, S. & Tokuoka, N. 2008 The study of spray structure by numerical simulation – the effect of interaction between droplets on spatial inhomogeneity. In 22nd European Conference on Liquid Atomization and Spray Systems 8–10 September 2008, Como Lake, Italy, ILASS-Europe.Google Scholar
Hinze, J. O. 1955 Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes. AIChE J. 1, 289–295.Google Scholar
Hishida, K., Ando, A. & Maeda, M. 1992 Experiments on particle dispersion in a turbulent mixing layer. Intl J. Multiphase Flow 18, 181–194.Google Scholar
Hopfinger, E. J. & Lasheras, J. C. 1996 Explosive breakup of a liquid jet by a swirling coaxial gas jet. Phys. Fluids 8, 1696–1698.Google Scholar
Hsiang, L.-P. & Faeth, G. M. 1992 Near-limit drop deformation and secondary breakup. Intl J. Multiphase Flow 18, 635–652.Google Scholar
Keane, R. D. & Adrian, R. J. 1990 Optimization of particle image velocimeters. I. Double pulsed systems. Meas. Sci. Technol. 1, 1202.Google Scholar
Khalitov, D. A. & Longmire, E. K. 2002 Simultaneous two-phase PIV by two-parameter phase discrimination. Exp. Fluids 32, 252–268.Google Scholar
Khalitov, D. A. & Longmire, E. K. 2003 Effect of particle size on velocity correlations in turbulent channel flow. In ASME/JSME 2003 4th Joint Fluids Summer Engineering Conference, pp. 445–453. American Society of Mechanical Engineers.Google Scholar
Kosiwczuk, W., Cessou, A., Trinite, M. & Lecordier, B. 2005 Simultaneous velocity field measurements in two-phase flows for turbulent mixing of sprays by means of two-phase PIV. Exp. Fluids 39, 895–908.Google Scholar
Kulick, J. D., Fessler, J. R. & Eaton, J. K. 1994 Particle response and turbulence modification in fully developed channel flow. J. Fluid Mech. 277, 109–134.Google Scholar
Lasheras, J. C. & Hopfinger, E. J. 2000 Liquid jet instability and atomization in a coaxial gas stream. Annu. Rev. Fluid Mech. 32, 275–308.Google Scholar
Lasheras, J. C., Villermaux, E. & Hopfinger, E. J. 1998 Break-up and atomization of a round water jet by a high-speed annular air jet. J. Fluid Mech. 357, 351–379.Google Scholar
Lazaro, B. J. & Lasheras, J. C. 1992 Particle dispersion in the developing free shear layer. Part 1. Unforced flow. J. Fluid Mech. 235, 143–178.Google Scholar
Lefebvre, A. H. 2010 Gas Turbine Combustion. CRC.Google Scholar
Liang, H. & Maxworthy, T. 2005 An experimental investigation of swirling jets. J. Fluid Mech. 525, 115–159.Google Scholar
Lilley, D. G. 1977 Swirl flows in combustion: a review. AIAA J. 15, 1063–1078.Google Scholar
Liu, A. B., Mather, D. & Reitz, R. D.1993 Modeling the effects of drop drag and breakup on fuel sprays. DTIC Document.Google Scholar
Longmire, E. K. & Eaton, J. K. 1992 Structure of a particle-laden round jet. J. Fluid Mech. 236, 217–257.Google Scholar
Loth, E., Tryggvason, G., Tsuji, Y., Elghobashi, S. E., Crowe, C. T., Berlemont, A., Reeks, M., Simonin, O., Frank, T., Onishi, Y. et al. 2006 Multiphase Flow Handbook. CRC.Google Scholar
Lozano, A., Barreras, F., Siegler, C. & Löw, D. 2005 The effects of sheet thickness on the oscillation of an air-blasted liquid sheet. Exp. Fluids 39, 127–139.Google Scholar
Lucca-Negro, O. & O’doherty, T. 2001 Vortex breakdown: a review. Prog. Energy Combust. Sci. 27, 431–481.Google Scholar
Marmottant, P. & Villermaux, E. 2004 On spray formation. J. Fluid Mech. 498, 73–111.CrossRefGoogle Scholar
Martinelli, F., Olivani, A. & Coghe, A. 2007 Experimental analysis of the precessing vortex core in a free swirling jet. Exp. Fluids 42, 827–839.Google Scholar
Mashayek, F. 1998 Droplet–turbulence interactions in low-Mach-number homogeneous shear two-phase flows. J. Fluid Mech. 367, 163–203.Google Scholar
Moin, P. & Apte, S. V. 2006 Large-eddy simulation of realistic gas turbine combustors. AIAA J. 44, 698–708.Google Scholar
Nicholls, J. A. & Ranger, A. A. 1969 Aerodynamic shattering of liquid drops. AIAA J. 7, 285–290.Google Scholar
Oweis, G. F., Van der Hout, I. E., Iyer, C., Tryggvason, G. & Ceccio, S. L. 2005 Capture and inception of bubbles near line vortices. Phys. Fluids 17, 022105.Google Scholar
Park, T. W., Katta, V. R. & Aggarwal, S. K. 1998 On the dynamics of a two-phase, nonevaporating swirling jet. Intl J. Multiphase Flow 24, 295–317.Google Scholar
Raffel, M., Willert, C. E., Wereley, S. & Kompenhans, J. 2013 Particle Image Velocimetry: A Practical Guide. Springer.Google Scholar
Rajamanickam, K. & Basu, S. 2017 Insights into the dynamics of spray–swirl interactions. J. Fluid Mech. 810, 82–126.Google Scholar
Ribeiro, M. M. & Whitelaw, J. H. 1980 Coaxial jets with and without swirl. J. Fluid Mech. 96, 769–795.Google Scholar
Saha, A., Lee, J. D., Basu, S. & Kumar, R. 2012 Breakup and coalescence characteristics of a hollow cone swirling spray. Phys. Fluids 24, 124103.Google Scholar
Sahu, S., Hardalupas, Y. & Taylor, A. 2014 Droplet–turbulence interaction in a confined polydispersed spray: effect of droplet size and flow length scales on spatial droplet–gas velocity correlations. J. Fluid Mech. 741, 98–138.Google Scholar
Sakakibara, J., Wicker, R. B. & Eaton, J. K. 1996 Measurements of the particle–fluid velocity correlation and the extra dissipation in a round jet. Intl J. Multiphase Flow 22, 863–881.Google Scholar
Sanadi, D., Rajamanickam, K. & Basu, S. 2017 Analysis of hollow cone spray injected in an unconfined, isothermal, co-annular swirling jet environment. Atomization and Sprays 27, 7–29.Google Scholar
Sankaran, V. & Menon, S. 2002 LES of spray combustion in swirling flows. J. Turbul. 3, 1–23.Google Scholar
Santhosh, R., Miglani, A. & Basu, S. 2014 Transition in vortex breakdown modes in a coaxial isothermal unconfined swirling jet. Phys. Fluids 26, 043601.Google Scholar
Sarpkaya, T. 1971 On stationary and travelling vortex breakdowns. J. Fluid Mech. 45, 545–559.Google Scholar
Schröder, A., Geisler, R., Staack, K., Elsinga, G. E., Scarano, F., Wieneke, B., Henning, A., Poelma, C. & Westerweel, J. 2011 Eulerian and Lagrangian views of a turbulent boundary layer flow using time-resolved tomographic PIV. Exp. Fluids 50, 1071–1091.CrossRefGoogle Scholar
Sciacchitano, A., Wieneke, B. & Scarano, F. 2013 PIV uncertainty quantification by image matching. Meas. Sci. Technol. 24, 045302.Google Scholar
Shirolkar, J. S., Coimbra, C. F. M. & McQuay, M. Q. 1996 Fundamental aspects of modeling turbulent particle dispersion in dilute flows. Prog. Energy Combust. Sci. 22, 363–399.Google Scholar
Simpkins, P. G. & Bales, E. L. 1972 Water-drop response to sudden accelerations. J. Fluid Mech. 55, 629–639.Google Scholar
Sirignano, W. A. 1999 Fluid Dynamics and Transport of Droplets and Sprays. Cambridge University Press.CrossRefGoogle Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Part I: coherent structures. Q. Appl. Maths 45, 561–571.Google Scholar
Squire, H. B. 1953 Investigation of the instability of a moving liquid film. Brit. J. Appl. Phys. 4, 167.Google Scholar
Sung, J. & Yoo, J. Y. 2001 Three-dimensional phase averaging of time-resolved PIV measurement data. Meas. Sci. Technol. 12, 655.Google Scholar
Syred, N. 2006 A review of oscillation mechanisms and the role of the precessing vortex core (PVC) in swirl combustion systems. Prog. Energy Combust. Sci. 32, 93–161.Google Scholar
Taylor, G. I. 1963 The shape and acceleration of a drop in a high speed air stream. In Scientific Papers of G. I. Taylor (ed. Batchelor, G. K.), vol. 3, pp. 457–464. Cambridge University Press.Google Scholar
Tropea, C., Yarin, A. L. & Foss, J. F. 2007 Springer Handbook of Experimental Fluid Mechanics. Springer.Google Scholar
Wang, H. Y., McDonell, V. G. & Samuelsen, S. 1993 Influence of hardware design on the flow field structures and the patterns of droplet dispersion: Part I – mean quantities. In ASME 1993 International Gas Turbine and Aeroengine Congress and Exposition, p. V03AT15A050. American Society of Mechanical Engineers.Google Scholar
Wang, S., Yang, V., Hsiao, G., Hsieh, S.-Y. & Mongia, H. C. 2007 Large-eddy simulations of gas-turbine swirl injector flow dynamics. J. Fluid Mech. 583, 1–10.CrossRefGoogle Scholar
Wieneke, B. 2015 PIV uncertainty quantification from correlation statistics. Meas. Sci. Technol. 26, 074002.Google Scholar

Rajamanickam supplementary movie 1

Flow field at Re=5089 and Re=33888

Download Rajamanickam supplementary movie 1(Video)
Video 20.8 MB

Rajamanickam supplementary movie 2

Droplet dispersion at MR=184 for ISL and OSL injections

Download Rajamanickam supplementary movie 2(Video)
Video 13.3 MB

Rajamanickam supplementary movie 3

Droplet dispersion at MR=450 for ISL and OSL injections

Download Rajamanickam supplementary movie 3(Video)
Video 13.1 MB

Rajamanickam supplementary movie 4

Droplet dispersion at MR=8164 for ISL and OSL injections

Download Rajamanickam supplementary movie 4(Video)
Video 16.4 MB

Rajamanickam supplementary movie 5

Droplet dispersion and corresponding flowfield streamlines at MR=8164 for ISL and OSL injections

Download Rajamanickam supplementary movie 5(Video)
Video 19.9 MB

Rajamanickam supplementary movie 6

Droplet breakup(Regime I) for MR=184, We=57

Download Rajamanickam supplementary movie 6(Video)
Video 6 MB

Rajamanickam supplementary movie 7

Droplet breakup(Regime II) for MR=450, We=100

Download Rajamanickam supplementary movie 7(Video)
Video 3.7 MB

Rajamanickam supplementary movie 8

Droplet breakup(Regime II) for MR=8164, We=500

Download Rajamanickam supplementary movie 8(Video)
Video 6.1 MB