Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-05-09T23:39:46.541Z Has data issue: false hasContentIssue false
  • English
  • Français

On the decay of dispersive motions in the outer region of rough-wall boundary layers

Published online by Cambridge University Press:  25 January 2019

Johan Meyers Open the ORCID record for Johan Meyers [Opens in a new window] ,
Bharathram Ganapathisubramani  and
Raúl Bayoán Cal
Johan Meyers*
Affiliation:
KU Leuven, Mechanical Engineering, Celestijnenlaan 300, B3001 Leuven, Belgium
Bharathram Ganapathisubramani
Affiliation:
University of Southampton, Aerodynamics and Flight Mechanics Group, Southampton SO17 1BJ, UK
Raúl Bayoán Cal
Affiliation:
Portland State University, Mechanical and Materials Engineering, Portland, OR 97207, USA
*
†Email address for correspondence: johan.meyers@kuleuven.be
Get access Rights & Permissions [Opens in a new window]

Abstract

In rough-wall boundary layers, wall-parallel non-homogeneous mean-flow solutions exist that lead to so-called dispersive velocity components and dispersive stresses. They play a significant role in the mean-flow momentum balance near the wall, but typically disappear in the outer layer. A theoretical framework is presented to study the decay of dispersive motions in the outer layer. To this end, the problem is formulated in Fourier space, and a set of governing ordinary differential equations per mode in wavenumber space is derived by linearizing the Reynolds-averaged Navier–Stokes equations around a constant background velocity. 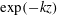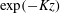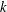With further simplifications, analytically tractable solutions are found consisting of linear combinations of $\exp (-kz)$ and $\exp (-Kz)$, with $z$ the wall distance, $k$ the magnitude of the horizontal wavevector 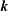$\boldsymbol{k}$, and where 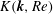$K(\boldsymbol{k},Re)$ is a function of 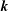$\boldsymbol{k}$ and the Reynolds number 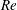$Re$. Moreover, for 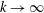$k\rightarrow \infty$ or 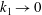$k_{1}\rightarrow 0$ (with 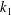$k_{1}$ the stream-wise wavenumber), 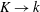$K\rightarrow k$ is found, in which case solutions consist of a linear combination of 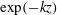$\exp (-kz)$ and 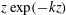$z\exp (-kz)$, and are independent of the Reynolds number. These analytical relations are compared in the limit of 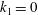$k_{1}=0$ to the rough boundary layer experiments by Vanderwel & Ganapathisubramani (J. Fluid Mech., vol. 774, 2015, R2) and are in reasonable agreement for 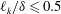$\ell _{k}/\unicode[STIX]{x1D6FF}\leqslant 0.5$, with 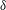$\unicode[STIX]{x1D6FF}$ the boundary-layer thickness and 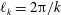$\ell _{k}=2\unicode[STIX]{x03C0}/k$.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 862 , 10 March 2019 , R5
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, W., Barros, J. M., Christensen, K. T. & Awasthi, A. 2015 Numerical and experimental study of mechanisms responsible for turbulent secondary flows in boundary layer flows over spanwise heterogeneous roughness. J. Fluid Mech. 768, 316–347.Google Scholar
Anderson, W. & Meneveau, C. 2011 Dynamic roughness model for large-eddy simulation of turbulent flow over multiscale, fractal-like rough surfaces. J. Fluid Mech. 679, 288–314.Google Scholar
Barros, J. M. & Christensen, K. T. 2014 Observations of turbulent secondary flows in a rough-wall boundary layer. J. Fluid Mech. 748, R1.Google Scholar
Castro, I. P. 2007 Rough-wall boundary layers: mean flow universality. J. Fluid Mech. 585, 469–485.Google Scholar
Chan, L., MacDonald, M., Chung, D., Hutchins, N. & Ooi, A. 2018 Secondary motion in turbulent pipe flow with three-dimensional roughness. J. Fluid Mech. 854, 5–33.Google Scholar
Deser, S. 1967 Covariant decomposition of symmetric tensors and the gravitational Cauchy problem. Ann. Inst. Henri Poincaré A 7, 149–188.Google Scholar
Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32 (1), 519–571.Google Scholar
Flack, K. A., Schultz, M. P. & Connelly, J. S. 2007 Examination of a critical roughness height for outer layer similarity. Phys. Fluids 19 (9), 095104.Google Scholar
Hwang, H. G. & Lee, J. H. 2018 Secondary flows in turbulent boundary layers over longitudinal surface roughness. Phys. Rev. Fluids 3, 014608.Google Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.Google Scholar
Jiménez, J. 2016 Optimal fluxes and Reynolds stresses. J. Fluid Mech. 809, 585–600.Google Scholar
Kevin, K., Monty, J. P., Bai, H. L., Pathikonda, G., Nugroho, B., Barros, J. M., Christensen, K. T. & Hutchins, N. 2017 Cross-stream stereoscopic particle image velocimetry of a modified turbulent boundary layer over directional surface pattern. J. Fluid Mech. 813, 412–435.Google Scholar
Manes, C., Pokrajac, D., Coceal, O. & McEwan, I. 2008 On the significance of form-induced stress in rough wall turbulent boundary layers. Acta Geophys. 56 (3), 845–861.Google Scholar
Medjnoun, T., Vanderwel, C. & Ganapathisubramani, B. 2018 Characteristics of turbulent boundary layers over smooth surfaces with spanwise heterogeneities. J. Fluid Mech. 838, 516–543.Google Scholar
Morgan, J. & McKeon, B. J. 2018 Relation between a singly-periodic roughness geometry and spatio-temporal turbulence characteristics. Intl J. Heat Fluid Flow 71, 322–333.Google Scholar
Nezu, I. & Nakagawa, H. 1984 Cellular secondary currents in straight conduit. J. Hydraul Engng ASCE 110 (2), 173–193.Google Scholar
Nikora, V., Goring, D., McEwan, I. & Griffiths, G. 2001 Spatially averaged open-channel flow over rough bed. J. Hydraul Engng ASCE 127 (2), 123–133.Google Scholar
Nikora, V., McEwan, I., McLean, S., Coleman, S., Pokrajac, D. & Walters, R. 2007 Double-averaging concept for rough-bed open-channel and overland flows: theoretical background. J. Hydraul Engng ASCE 133 (8), 873–883.Google Scholar
Prasad, A. K. 2000 Stereoscopic particle image velocimetry. Exp. Fluids 29 (2), 103–116.Google Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44 (1), 1–25.Google Scholar
Raupach, M. R. & Shaw, R. H. 1982 Averaging procedures for flow within vegetation canopies. Boundary-Layer Meteorology 22 (1), 79–90.Google Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.Google Scholar
Townsend, A. A. 1956 The Structure of Turbulent Shear Flow, 1st edn. Cambridge University Press.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Vanderwel, C. & Ganapathisubramani, B. 2015 Effects of spanwise spacing on large-scale secondary flows in rough-wall turbulent boundary layers. J. Fluid Mech. 774, R2.Google Scholar
Wang, Z.-Q. & Cheng, N.-S. 2005 Secondary flows over artificial bed strips. Adv. Water Resour. 28 (5), 441–450.Google Scholar
Wu, J.-Z., Zhou, Y. & Wu, J.-M.1996 Reduced stress tensor and dissipation and the transport of Lamb vector. Tech. Rep. 96-21, ICASE.Google Scholar
Yang, J. & Anderson, W. 2018 Numerical study of turbulent channel flow over surfaces with variable spanwise heterogeneities: topographically-driven secondary flows affect outer-layer similarity of turbulent length scales. Flow Turbul. Combust. 100 (1), 1–17.Google Scholar