Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-25T07:29:55.631Z Has data issue: false hasContentIssue false
  • English
  • Français

On precessing flow in an oblate spheroid of arbitrary eccentricity

Published online by Cambridge University Press:  05 March 2014

Keke Zhang ,
Kit H. Chan  and
Xinhao Liao
Keke Zhang*
Affiliation:
Department of Mathematical Sciences, University of Exeter, Exeter EX4 4QF, UK
Kit H. Chan
Affiliation:
Department of Mathematics, University of Hong Kong, Pokfulam, Hong Kong
Xinhao Liao
Affiliation:
Key Laboratory of Planetary Sciences, Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai 200030, China
*
†Email address for correspondence: kzhang@ex.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a homogeneous fluid of viscosity $\nu $ confined within an oblate spheroidal cavity of arbitrary eccentricity 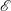$\mathcal{E}$ marked by the equatorial radius 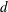$d$ and the polar radius 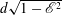$d \sqrt{1-\mathcal{E}^2}$ with 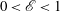$0<\mathcal{E}<1$. The spheroidal container rotates rapidly with an angular velocity 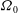${\boldsymbol{\Omega}}_0 $ about its symmetry axis and precesses slowly with an angular velocity 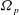${\boldsymbol{\Omega}}_p$ about an axis that is fixed in space. It is through both topographical and viscous effects that the spheroidal container and the viscous fluid are coupled together, driving precessing flow against viscous dissipation. The precessionally driven flow is characterized by three dimensionless parameters: the shape parameter 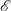$\mathcal{E}$, the Ekman number 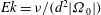${\mathit{Ek}}=\nu /(d^2 \delimiter "026A30C {\boldsymbol{\Omega}}_0\delimiter "026A30C )$ and the Poincaré number 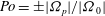${\mathit{Po}}=\pm \delimiter "026A30C {\boldsymbol{\Omega}}_p\delimiter "026A30C / \delimiter "026A30C \boldsymbol{\Omega}_0\delimiter "026A30C $. We derive a time-dependent asymptotic solution for the weakly precessing flow in the mantle frame of reference satisfying the no-slip boundary condition and valid for a spheroidal cavity of arbitrary eccentricity at 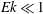${\mathit{Ek}}\ll 1$. No prior assumptions about the spatial–temporal structure of the precessing flow are made in the asymptotic analysis. We also carry out direct numerical simulation for both the weakly and the strongly precessing flow in the same frame of reference using a finite-element method that is particularly suitable for non-spherical geometry. A satisfactory agreement between the asymptotic solution and direct numerical simulation is achieved for sufficiently small Ekman and Poincaré numbers. When the nonlinear effect is weak with 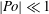$\delimiter "026A30C {\mathit{Po}}\delimiter "026A30C \ll 1$, the precessing flow in an oblate spheroid is characterized by an azimuthally travelling wave without having a mean azimuthal flow. Stronger nonlinear effects with increasing 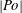$\delimiter "026A30C {\mathit{Po}}\delimiter "026A30C $ produce a large-amplitude, time-independent mean azimuthal flow that is always westward in the mantle frame of reference. Implications of the precessionally driven flow for the westward motion observed in the Earth’s fluid core are also discussed.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Rotating flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 743 , 25 March 2014 , pp. 358 - 384
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Boisson, J., Cébron, D. C., Moisy, F. & Cortet, P.-P. 2012 Earth rotation prevents exact solid-body rotation of fluids in the laboratory. Europhys. Lett. 98, 59002.CrossRefGoogle Scholar
Bullard, E. C. 1949 The magnetic flux within the earth. Proc. R. Soc. Lond. A 197, 433–453.Google Scholar
Busse, F. H. 1968 Steady fluid flow in a precessing spheroidal shell. J. Fluid Mech. 136, 739–751.CrossRefGoogle Scholar
Cébron, D. C., Le Bars, M. & Meunier, P. 2010 Tilt-over mode in a precessing triaxial ellipsoid. Phys. Fluids 22, 116601.CrossRefGoogle Scholar
Chan, K., Zhang, K. & Liao, X. 2010 An EBE finite element method for simulating nonlinear flows in rotating spheroidal cavities. Intl J. Numer. Meth. Fluids 63, 395–414.CrossRefGoogle Scholar
Cui, Z., Zhang, K. & Liao, X. 2014 On the completeness of inertial wave modes in rotating annular channels. Geophys. Astrophys. Fluid Dyn. 108, 44–59.CrossRefGoogle Scholar
Dwyer, C. A., Stevenson, D. J. & Nimmo, F. 2011 A long-lived lunar dynamo driven by continuous mechanical stirring. Nature 479, 212–214.CrossRefGoogle ScholarPubMed
Goto, S., Ishii, N., Kida, S. & Nishioka, M. 2007 Turbulence generator using a precessing sphere. Phys. Fluids 19, 061705.CrossRefGoogle Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Hollerbach, R. & Kerswell, R. R. 1995 Oscillatory internal shear layers in rotating and precessing flows. J. Fluid Mech. 298, 327–339.CrossRefGoogle Scholar
Hollerbach, R., Nore, C., Marti, P., Vantieghem, S., Luddens, F. & Léorat, J. 2013 Parity-breaking flows in precessing spherical containers. Phys. Rev. E 87, 053020.CrossRefGoogle ScholarPubMed
Kerswell, R. R. 1993 The instability of precessing flow. Geophys. Astrophys. Fluid Dyn. 72, 107–144.CrossRefGoogle Scholar
Kerswell, R. R. 1996 Upper bounds on the energy dissipation in turbulent precession. J. Fluid Mech. 321, 335–370.CrossRefGoogle Scholar
Kida, S. 2011 Steady flow in a rapidly rotating sphere with weak precession. J. Fluid Mech. 680, 150–193.CrossRefGoogle Scholar
Kong, D., Zhang, K. & Schubert, G. 2010 Shapes of two-layer models of rotating planets. J. Geophys. Res. 115, E12003.Google Scholar
Kong, D., Zhang, K., Schubert, G. & Anderson, J. 2013 A three-dimensional numerical solution for the shape of a rotationally distorted polytrope of index unity. Astrophys. J. 763, 116.CrossRefGoogle Scholar
Liao, X. & Zhang, K. 2012a On flow in weakly precessing cylinders: the general asymptotic solution. J. Fluid Mech. 709, 610–621.CrossRefGoogle Scholar
Liao, X. & Zhang, K. 2012b Asymptotic solutions of differential rotation driven by convection in rapidly rotating fluid spheres with the non-slip boundary condition. Geophys. Astrophys. Fluid Dyn. 692, 420–445.Google Scholar
Lorenzani, S. & Tilgner, A. 2001 Fluid instabilities in precessing spheroidal cavities. J. Fluid Mech. 447, 111–128.CrossRefGoogle Scholar
Lorenzani, S. & Tilgner, A. 2003 Inertial instabilities of fluid flow in precessing spheroidal shells. J. Fluid Mech. 492, 363–379.CrossRefGoogle Scholar
Malkus, W. V. R. 1968 Precession of the earth as the cause of geomagnetism. Science 136, 259–264.CrossRefGoogle Scholar
Noir, J., Cardin, P., Jault, D. & Masson, J. P. 2003 Experimental evidence of non-linear resonance effects between retrograde precession and the tilt-over mode within a spheroid. Geophys. J. Intl 154, 407–416.CrossRefGoogle Scholar
Noir, J., Jault, D. & Cardin, P. 2001 Numerical study of the motions within a slowly precessing sphere at low Ekman number. J. Fluid Mech. 437, 283–299.CrossRefGoogle Scholar
Poincaré, H. 1910 Sur la précession des corps déformables. Bull. Astron. 27, 321–356.CrossRefGoogle Scholar
Pozzo, M., Davies, C., Gubbins, D. & Alfe, D. 2012 Thermal and electrical conductivity of iron at Earth’s core conditions. Nature 458, 355–358.CrossRefGoogle Scholar
Roberts, P. H. & Stewartson, K. 1965 On the motion of a liquid in a spheroidal cavity of a precessing rigid body: II. Math. Proc. Camb. Phil. Soc. 61, 279–288.CrossRefGoogle Scholar
Stewartson, K. & Roberts, P. H. 1963 On the motion of a liquid in a spheroidal cavity of a precessing rigid body. J. Fluid Mech. 17, 1–20.CrossRefGoogle Scholar
Tilgner, A. 2005 Precession driven dynamos. Phys. Fluids 17, 034104–034106.CrossRefGoogle Scholar
Tilgner, A. 2007 Rotational dynamics of the core. In Core Dynamics (ed. Schubert, G), Treatise of Geophysics, vol. 8, pp. 207–243. Elsevier.Google Scholar
Tilgner, A. & Busse, F. H. 2001 Fluid flows in precessing spherical shells. J. Fluid Mech. 426, 387–396.CrossRefGoogle Scholar
Triana, S. A., Zimmerman, D. S. & Lathrop, D. P. 2012 Precessional states in a laboratory model of the Earth’s core. J. Geophys. Res. 117, B04103.Google Scholar
Vanyo, J. P. & Likins, P. W. 1972 Rigid-body approximation to turbulent motion in a liquid-fillled, precessing, spherical cavity. J. Appl. Mech. 39, 19–24.CrossRefGoogle Scholar
Vanyo, J. P., Wilde, P., Cardin, P. & Olson, P. 1995 Experiments on precessing flows in the Earth’s liquid core. Geophys. J. Intl 121, 136–142.CrossRefGoogle Scholar
Wei, X. & Tilgner, A. 2013 Stratified precessional flow in spherical geometry. J. Fluid Mech. 718, R2 doi: http://dx.doi.org/10.1017/jfm.2013.68.CrossRefGoogle Scholar
Wu, C. C. & Roberts, P. H. 2009 On a dynamo driven by topographic precession. Geophys. Astrophys. Fluid Dyn. 103, 467–501.CrossRefGoogle Scholar
Zhang, K. 1992 Spiralling columnar convection in rapidly rotating spherical fluid shells. J. Fluid Mech. 236, 535–556.CrossRefGoogle Scholar
Zhang, K., Chan, K. & Liao, X. 2010 On fluid flows in precessing spheres in the mantle frame of reference. Phys. Fluids 22, 116604.CrossRefGoogle Scholar
Zhang, K., Liao, X. & Earnshaw, P. 2004 On inertial waves and oscillations in a rapidly rotating fluid spheroid. J. Fluid Mech. 504, 1–40.CrossRefGoogle Scholar