Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T08:15:48.776Z Has data issue: false hasContentIssue false
  • English
  • Français

On non-self-similar regimes in homogeneous isotropic turbulence decay

Published online by Cambridge University Press:  11 September 2012

Marcello Meldi  and
Pierre Sagaut
Marcello Meldi*
Affiliation:
Institut Jean Le Rond d’Alembert, UMR 7190, 4 Place Jussieu, Case 162, Université Pierre et Marie Curie, Paris 6, F-75252 Paris CEDEX 5, France
Pierre Sagaut
Affiliation:
Institut Jean Le Rond d’Alembert, UMR 7190, 4 Place Jussieu, Case 162, Université Pierre et Marie Curie, Paris 6, F-75252 Paris CEDEX 5, France
*
†Email address for correspondence: marcellomeldi@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Both theoretical analysis and eddy-damped quasi-normal Markovian (EDQNM) simulations are carried out to investigate the different decay regimes of an initially non-self-similar isotropic turbulence. Breakdown of self-similarity is due to the consideration of a composite three-range energy spectrum, with two different slopes at scales larger than the integral length scale. It is shown that, depending on the initial conditions, the solution can bifurcate towards a true self-similar decay regime, or sustain a non-self-similar state over an arbitrarily long time. It is observed that these non-self-similar regimes cannot be detected, restricting the observation to time exponents of global quantities such as kinetic energy or dissipation. The actual reason is that the decay is controlled by large scales close to the energy spectrum peak. This theoretical prediction is assessed by a detailed analysis of triadic energy transfers, which show that the largest scales have a negligible impact on the total transfers. Therefore, it is concluded that details of the energy spectrum near the peak, which may be related to the turbulence production mechanisms, are important. Since these mechanisms are certainly not universal, this may at least partially explain the significant discrepancies that exist between experimental data and theoretical predictions. Another conclusion is that classical self-similarity theories, which connect the asymptotic behaviour of either the energy spectrum 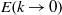or the velocity correlation function 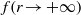and the turbulence decay exponent, are not particularly relevant when the large-scale spectrum shape exhibits more than one range.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 711 , 25 November 2012 , pp. 364 - 393
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
2. Bos, W. J. T., Shao, L. & Bertoglio, J. P. 2007 Spectral imbalance and the normalized dissipation rate of turbulence. Phys. Fluids 19, 045101.CrossRefGoogle Scholar
3. Cambon, C., Mansour, N. N. & Godeferd, F. S. 1997 Energy transfer in rotating turbulence. J. Fluid Mech. 337, 303–332.CrossRefGoogle Scholar
4. Clark, T. T. & Zemach, C. 1998 Symmetries and the approach to statistical equilibrium in isotropic turbulence. Phys. Fluids 10 (11), 2846–2858.CrossRefGoogle Scholar
5. Comte-Bellot, G. & Corrsin, S. 1966 The use of a contraction to improve the isotropy of grid-generated turbulence. J. Fluid Mech. 25, 657–682.CrossRefGoogle Scholar
6. Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
7. Davidson, P. A. 2009 The role of angular momentum conservation in homogeneous turbulence. J. Fluid Mech. 632, 329–358.CrossRefGoogle Scholar
8. Davidson, P. A. 2011 The minimum energy decay rate in quasi-isotropic grid turbulence. Phys. Fluids 23, 085108.CrossRefGoogle Scholar
9. Eyink, G. L. & Thomson, D. J. 2000 Free decay of turbulence and breakdown of self-similarity. Phys. Fluids 12 (3), 477–479.CrossRefGoogle Scholar
10. Frenkel, A. L. 1984 Decay of homogeneous turbulence in three-range models. Phys. Lett. A 102 (7), 298–302.CrossRefGoogle Scholar
11. Frenkel, A. L. & Levich, E. 1983 ‘Statistical helicity invariant’ and decay of inertial turbulence. Phys. Lett. A 98 (1–2), 25–27.CrossRefGoogle Scholar
12. Frisch, U., Lesieur, M. & Schertzer, D. 1980 Comments on the quasi-normal Markovian approximation for fully-developed turbulence. J. Fluid Mech. 97, 181–192.CrossRefGoogle Scholar
13. George, W. K. 1992 The decay of homogeneous isotropic turbulence. Phys. Fluids A 4 (7), 1492–1509.CrossRefGoogle Scholar
14. George, W. K. & Wang, H. 2009 The exponential decay of homogeneous turbulence. Phys. Fluids A 21, 025108.CrossRefGoogle Scholar
15. Hinze, J. O. 1975 Turbulence. McGraw-Hill Series in Mechanical Engineering , 790 pages.Google Scholar
16. Huang, M. J. & Leonard, A. 1994 Power-law decay of homogeneous turbulence at low Reynolds numbers. Phys. Fluids 6, 3765–3775.CrossRefGoogle Scholar
17. Ishida, T., Davidson, P. A. & Kaneda, Y. 2006 On the decay of isotropic turbulence. J. Fluid Mech. 564, 455–475.CrossRefGoogle Scholar
18. Kolmogorov, A. N. 1941 On the degeneration of isotropic turbulence in an incompressible viscous fluid. Dokl. Akad. Nauk SSSR 31 (6), 538–541.Google Scholar
19. Krogstad, P.-Å. & Davidson, P. A. 2010 Is grid turbulence Saffman turbulence? J. Fluid Mech. 642, 373–394.CrossRefGoogle Scholar
20. Krogstad, P.-Å. & Davidson, P. A. 2011 Freely decaying, homogeneous turbulence generated by multi-scale grids. J. Fluid Mech. 680, 417–434.CrossRefGoogle Scholar
21. Krogstad, P.-Å. & Davidson, P. A. 2012 Near-field investigation of turbulence produced by multi-scale grids. Phys. Fluids 24, 035103.CrossRefGoogle Scholar
22. Lesieur, M. & Schertzer, D. 1978 Self similar decay of high Reynolds number turbulence. J. de Mécanique 17 (4), 609–646.Google Scholar
23. Lesieur, M. 2008 Turbulence in Fluids, 4th edn. Springer.CrossRefGoogle Scholar
24. Llor, A. 2011 Langevin equation of big structure dynamics in turbulence: Landau’s invariant in the decay of homogeneous isotropic turbulence. Eur. J. Mech. B 30, 480–504.CrossRefGoogle Scholar
25. Mansour, N. N. & Wray, A. A. 1994 Decay of isotropic turbulence at low Reynolds number. Phys. Fluids 6, 808–814.CrossRefGoogle Scholar
26. Mazellier, N. & Vassilicos, J. C. 2010 Turbulence without Richardson-like cascade. Phys. Fluids 22, 075101.CrossRefGoogle Scholar
27. Meldi, M., Sagaut, P. & Lucor, D. 2011 A stochastic view of isotropic turbulence decay. J. Fluid Mech. 668, 351–362.CrossRefGoogle Scholar
28. Mohamed, M. S. & LaRue, J. C. 1990 The decay power law in grid-generated turbulence. J. Fluid Mech. 219, 195–214.CrossRefGoogle Scholar
29. Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics: Mechanics of Turbulence, vol. 2. MIT Press.Google Scholar
30. Oberlack, M. 2002 On the decay exponent of isotropic turbulence. Proc. Appl. Math. Mech. 1, 294–297.3.0.CO;2-W>CrossRefGoogle Scholar
31. Orszag, S. A. 1970 Analytical theories of turbulence. J. Fluid Mech. 41, 363–386.CrossRefGoogle Scholar
32. Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
33. Ristorcelli, J. R. 2003 The self-preserving decay of isotropic turbulence: analytic solutions for energy and dissipation. Phys. Fluids 15, 3248–3250.CrossRefGoogle Scholar
34. Ristorcelli, J. R. 2006 Passive scalar mixing: analytic study of time scale ratio, variance and mix rate. Phys. Fluids 18, 075101.CrossRefGoogle Scholar
35. Ristorcelli, J. R. & Livescu, D. 2004 Decay of isotropic turbulence: fixed points and solutions for non-constant palinstrophy. Phys. Fluids 16, 3487–3490.CrossRefGoogle Scholar
36. Saffman, P. J. 1967 The large-scale structure of homogeneous turbulence. J. Fluid Mech. 27, 581–593.CrossRefGoogle Scholar
37. Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence Dynamics. Cambridge University Press.CrossRefGoogle Scholar
38. Skrbek, L. & Stalp, S. R. 2000 On the decay of homogeneous isotropic turbulence. Phys. Fluids 12, 1997–2019.CrossRefGoogle Scholar
39. Speziale, C. G. & Bernard, P. S. 1992 The energy decay in self-preserving isotropic turbulence revisited. J. Fluid Mech. 241, 645–667.CrossRefGoogle Scholar
40. Taylor, G. I. 1935 Statistical theory of turbulence. Proc. R. Soc. Lond. A 151, 421–444.CrossRefGoogle Scholar
41. Tchoufag, J., Sagaut, P. & Cambon, C. 2012 Spectral approach to finite Reynolds number effects on Kolmogorov’s law in isotropic turbulence. Phys. Fluids 24, 015107.CrossRefGoogle Scholar
42. Vassilicos, J. C. 2011 An infinity of possible invariants for decaying homogeneous turbulence. Phys. Lett. A 375, 1010–1013.CrossRefGoogle Scholar
43. Valente, P. C. & Vassilicos, J. C. 2012 Dependence of decaying homogeneous isotropic turbulence on inflow conditions. Phys. Lett. A 376, 510–514.CrossRefGoogle Scholar