Published online by Cambridge University Press: 29 April 2013
Rayleigh–Bénard convection in glycerol (Prandtl number 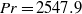 $\mathit{Pr}= 2547. 9$) in a cylindrical cell with an aspect ratio of
$\mathit{Pr}= 2547. 9$) in a cylindrical cell with an aspect ratio of 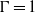 $\Gamma = 1$ was studied by means of three-dimensional direct numerical simulations (DNS). For that purpose, we implemented temperature-dependent material properties into our DNS code, by prescribing polynomial functions up to seventh order for the viscosity, the heat conductivity and the density. We performed simulations with the common Oberbeck–Boussinesq (OB) approximation and with non-Oberbeck–Boussinesq (NOB) effects within a range of Rayleigh numbers of
$\Gamma = 1$ was studied by means of three-dimensional direct numerical simulations (DNS). For that purpose, we implemented temperature-dependent material properties into our DNS code, by prescribing polynomial functions up to seventh order for the viscosity, the heat conductivity and the density. We performed simulations with the common Oberbeck–Boussinesq (OB) approximation and with non-Oberbeck–Boussinesq (NOB) effects within a range of Rayleigh numbers of 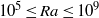 $1{0}^{5} \leq \mathit{Ra}\leq 1{0}^{9} $. For the highest temperature differences,
$1{0}^{5} \leq \mathit{Ra}\leq 1{0}^{9} $. For the highest temperature differences, 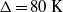 $\Delta = 80~\mathrm{K} $, the viscosity at the top is
$\Delta = 80~\mathrm{K} $, the viscosity at the top is  ${\sim }360\hspace{0.167em} \% $ times higher than at the bottom, while the differences of the other material properties are less than
${\sim }360\hspace{0.167em} \% $ times higher than at the bottom, while the differences of the other material properties are less than 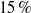 $15\hspace{0.167em} \% $. We analysed the temperature and velocity profiles and the thermal and viscous boundary-layer thicknesses. NOB effects generally lead to a breakdown of the top–bottom symmetry, typical for OB Rayleigh–Bénard convection. Under NOB conditions, the temperature in the centre of the cell
$15\hspace{0.167em} \% $. We analysed the temperature and velocity profiles and the thermal and viscous boundary-layer thicknesses. NOB effects generally lead to a breakdown of the top–bottom symmetry, typical for OB Rayleigh–Bénard convection. Under NOB conditions, the temperature in the centre of the cell 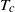 ${T}_{c} $ increases with increasing
${T}_{c} $ increases with increasing 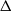 $\Delta $ and can be up to
$\Delta $ and can be up to 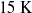 $15~\mathrm{K} $ higher than under OB conditions. The comparison of our findings with several theoretical and empirical models showed that two-dimensional boundary-layer models overestimate the actual
$15~\mathrm{K} $ higher than under OB conditions. The comparison of our findings with several theoretical and empirical models showed that two-dimensional boundary-layer models overestimate the actual 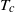 ${T}_{c} $, while models based on the temperature or velocity scales predict
${T}_{c} $, while models based on the temperature or velocity scales predict 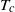 ${T}_{c} $ very well with a standard deviation of
${T}_{c} $ very well with a standard deviation of 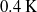 $0. 4~\mathrm{K} $. Furthermore, the obtained temperature profiles bend closer towards the cold top plate and further away from the hot bottom plate. The situation for the velocity profiles is reversed: they bend farther away from the top plate and closer towards to the bottom plate. The top boundary layers are always thicker than the bottom ones. Their ratio is up to 2.5 for the thermal and up to 4.5 for the viscous boundary layers. In addition, the Reynolds number
$0. 4~\mathrm{K} $. Furthermore, the obtained temperature profiles bend closer towards the cold top plate and further away from the hot bottom plate. The situation for the velocity profiles is reversed: they bend farther away from the top plate and closer towards to the bottom plate. The top boundary layers are always thicker than the bottom ones. Their ratio is up to 2.5 for the thermal and up to 4.5 for the viscous boundary layers. In addition, the Reynolds number 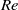 $\mathit{Re}$ and the Nusselt number
$\mathit{Re}$ and the Nusselt number 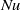 $\mathit{Nu}$ were investigated:
$\mathit{Nu}$ were investigated: 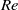 $\mathit{Re}$ is higher and
$\mathit{Re}$ is higher and 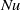 $\mathit{Nu}$ is lower under NOB conditions. The Nusselt number
$\mathit{Nu}$ is lower under NOB conditions. The Nusselt number 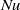 $\mathit{Nu}$ is influenced in a nonlinear way by NOB effects, stronger than was suggested by the two-dimensional simulations. The actual scaling of
$\mathit{Nu}$ is influenced in a nonlinear way by NOB effects, stronger than was suggested by the two-dimensional simulations. The actual scaling of 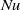 $\mathit{Nu}$ with
$\mathit{Nu}$ with 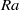 $\mathit{Ra}$ in the NOB case is
$\mathit{Ra}$ in the NOB case is 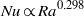 $\mathit{Nu}\propto {\mathit{Ra}}^{0. 298} $ and is in excellent agreement with the experimental data.
$\mathit{Nu}\propto {\mathit{Ra}}^{0. 298} $ and is in excellent agreement with the experimental data.