Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-18T08:58:55.710Z Has data issue: false hasContentIssue false
  • English
  • Français

On models for predicting thermodynamic regimes in high-pressure turbulent mixing and combustion of multispecies mixtures

Published online by Cambridge University Press:  23 March 2018

Giacomo Castiglioni  and
Josette Bellan Open the ORCID record for Josette Bellan [Opens in a new window]
Giacomo Castiglioni
Affiliation:
California Institute of Technology, Mechanical and Civil Engineering Department, Pasadena, CA 91125, USA
Josette Bellan*
Affiliation:
California Institute of Technology, Mechanical and Civil Engineering Department, Pasadena, CA 91125, USA Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109, USA
*
†Email address for correspondence: josette.bellan@jpl.nasa.gov
Get access Rights & Permissions [Opens in a new window]

Abstract

The thermodynamic regime of a complex mixture depends on the composition, the pressure and the temperature; the spinodal locus separates the regime of thermodynamic instability from the remainder of the phase space. Since diffusion is one of the phenomena affecting the local chemical composition, the first focus is here on evaluating diffusion models in the context of high-pressure (high-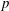$p$) multispecies mixing and combustion. It is shown that the diffusion model equations previously used to create two high-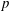$p$ direct numerical simulation (DNS) databases can reproduce classical experimental observations of uphill diffusion in an accurate spatiotemporal manner, whereas the popular model which has a diagonal diffusion matrix and uses a velocity correction lacks spatiotemporal accuracy. Further, a mathematical formalism is used to compute the spinodal locus for mixtures for which either experimental data or previous computations from the literature are available, and it is shown that the agreement of the present calculations with that previously existing information is excellent. Using the spinodal-calculation mathematical formalism, the aforementioned DNS databases are then examined to determine the thermodynamic regime of the mixture at important stages of the simulations. In the first subset of the DNS databases that portrays mixing of five species under high-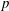$p$ conditions, this stage is that of the transitional state representing the individual time station at which each simulation, having been initiated in a laminar state, transitions to a state having turbulent characteristics. In the second subset of the DNS databases that portrays high-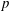$p$ turbulent combustion, this stage represents the individual time station at the peak 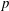$p$ achieved during the calculations. In both databases, the influence of the initial Reynolds number, the free-stream composition and the free-stream 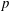$p$ is studied. The results show that in all cases the mixture is in the single-phase regime. The present DNS databases have only five species, but it is shown that the methodology for computing the spinodal locus can be applied to very complex mixtures, with examples given for a twelve-species mixture and surrogate diesel fuels, thereby boding well for determining the thermodynamic regime of practical mixtures in high-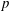$p$ turbulent flow simulations for engineering applications. According to these calculations, diesel-fuel surrogates are always in the single-phase regime at injection-conditions 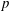$p$ and temperatures existing in diesel-engine combustion chambers.

JFM classification

Mixing: Mixing Mixing: Turbulent mixing Reacting Flows: Turbulent reacting flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 843 , 25 May 2018 , pp. 536 - 574
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abu-Eishah, S. I., Darwish, N. A. & Aljundi, I. H. 1998 Prediction of critical properties of binary mixtures using the prsv-2 equation of state. Intl J. Thermophys. 19 (1), 239–258.Google Scholar
Bellan, J. 2017 Direct numerical simulation of a high-pressure turbulent reacting mixing layer. Combust. Flame 176, 245–262.Google Scholar
Chehroudi, B., Talley, D. G. & Coy, E. 2002 Visual characteristics and initial growth rates of round cryogenic jets at subcritical and supercritical pressures. Phys. Fluids 14, 850–860.Google Scholar
Crua, C., Heikal, M. R. & Gold, M. R. 2015 Microscopic imaging of the initial stage of diesel spray formation. Fuel 157, 140–150.Google Scholar
Crua, C., Manin, J. & Pickett, L. M. 2017 On the transcritical mixing of fuels at diesel engine conditions. Fuel 208, 535–548.Google Scholar
De Groot, S. R. & Mazur, P. 1984 Non-equilibrium Thermodynamics. Dover.Google Scholar
Debenedetti, P. G. 1996 Metastable Liquids: Concepts and Principles. Princeton University Press.Google Scholar
Desantes, J. M., Pastor, J. V., Garcia-Oliver, J. M. & Briceno, F. J. 2014 An experimental analysis on the evolution of the transient tip penetration in reacting diesel sprays. Combust. Flame 161, 2137–2150.Google Scholar
Duncan, J. B. & Toor, H. L. 1962 An experimental study of three component gas diffusion. AIChE J. 8 (1), 38–41.Google Scholar
Ern, A. & Giovangigli, V. 1998 Thermal diffusion effects in hydrogen–air and methane–air flames. Combust. Theor. Model. 2 (4), 349–372.Google Scholar
Ern, A. & Giovangigli, V. 1999 Impact of detailed multicomponent transport on planar and counterflow hydrogen/air and methane/air flames. Combust. Sci. Technol. 149 (1–6), 157–181.Google Scholar
Falgout, Z., Rahm, M., Sedarsky, D. & Linne, M. 2016 Gas/fuel jet interfaces under high pressures and temperatures. Fuel 168, 14–21.Google Scholar
Hannoun, I. A., Fernando, H. J. S. & List, E. J. 1988 Turbulence structure near a sharp density interface. J. Fluid Mech. 189, 189–209.Google Scholar
Harstad, K. & Bellan, J. 2004a High-pressure binary mass diffusion coefficients for combustion applications. Ind. Engng Chem. Res. 43 (2), 645–654.Google Scholar
Harstad, K. G. & Bellan, J. 2004b Mixing rules for multicomponent mixture mass diffusion coefficients and thermal diffusion factors. J. Chem. Phys. 120 (12), 5664–5673.Google Scholar
Harstad, K. G., Miller, R. S. & Bellan, J. 1997 Efficient high-pressure state equations. AIChE. J. 43 (6), 1605–1610.Google Scholar
Heidemann, R. A. & Khalil, A. M. 1980 The calculation of critical points. AIChE J. 26 (5), 769–779.Google Scholar
Hirschfelder, J. O., Curtiss, C. F. & Bird, R. B. 1964 Molecular Theory of Gases and Liquids. Wiley.Google Scholar
Jones, W. W. & Boris, J. P. 1981 An algorithm for multispecies diffusion fluxes. Computers & Chemistry 5 (2–3), 139–146.Google Scholar
Knapp, H., Döring, R., Oellrich, L., Plöcker, U. & Prausnitz, J. M. 1982 Vapor–liquid Equilibria for Mixtures of Low Boiling Substances, vol. VI. Dechema.Google Scholar
Krishna, R. 2015 Uphill diffusion in multicomponent mixtures. Chem. Soc. Rev. 44 (10), 2812–2836.Google Scholar
Lawal., A. S. 1987 A consistent rule for selecting roots in cubic equations of state. Ind. Engng Chem. Res. 26 (4), 857–859.Google Scholar
Lemmon, E. W., Huber, M. L. & McLinden, M. O. 2013 NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties – REFPROP, Version 9.1, National Institute of Standards and Technology.Google Scholar
Lin, R. & Tavlarides, L. L. 2012 Thermophysical properties needed for the development of the supercritical diesel combustion technology: evaluation of diesel fuel surrogate models. J. Supercritical Fluids 71, 136–146.Google Scholar
Linne, M. 2013 Imaging in the optically dense regions of a spray: a review of developing techniques. Prog. Energy Combust. Sci. 39 (5), 403–440.Google Scholar
Manin, J., Bardi, M., Pickett, L., Dahms, R. & Oefelein, J. 2014 Microscopic investigation of the atomization and mixing processes of diesel sprays injected into high pressure and temperature environments. Fuel 134, 531–543.Google Scholar
Marrero, T. R. & Mason, E. A. 1972 Gaseous diffusion coefficients. J. Phys. Chem. Ref. Data 1 (1), 3–118.Google Scholar
Masi, E., Bellan, J., Harstad, K. G. & Okong’o, N. A. 2013 Multi-species turbulent mixing under supercritical-pressure conditions: modelling, direct numerical simulation and analysis revealing species spinodal decomposition. J. Fluid Mech. 721, 578–626.Google Scholar
Mayer, W., Schik, A., Schweitzer, C. & Schaeffler, M.1996 Injection and mixing processes in high pressure LOX/GH2 rocket. AIAA Paper 96-2620.Google Scholar
Mayer, W. & Tamura, H. 1996 Propellant injection in a liquid oxygen/gaseous hydrogen rocket engine. J. Propul. Power 12, 1137–1147.Google Scholar
Mueller, C. J., Cannella, W. J., Bays, J. T., Bruno, T. J., DeFabio, K., Dettman, H. D., Gieleciak, R. M., Huber, M. L., Kweon, C.-B., McConnell, S. S. et al. 2016 Diesel surrogate fuels for engine testing and chemical-kinetic modeling: compositions and properties. Energy Fuels 30, 1445–1451.Google Scholar
Musculus, M. P. B. & Kattke, K.2009 Entrainment waves in diesel jets. SAE Paper No. 2009-01-1355.Google Scholar
Nauman, E. B. & He, D. Q. 2001 Nonlinear diffusion and phase separation. Chem. Engng Sci. 56, 1999–2018.Google Scholar
Nichita, D. V. & Gomez, S. 2010 Efficient and reliable mixture critical points calculation by global optimization. Fluid Phase Equilib. 291 (2), 125–140.Google Scholar
Oschwald, M. & Schick, A. 1999 Supercritical nitrogen free jet investigated by spontaneous Raman scattering. Exp. Fluids. 27, 497–506.Google Scholar
Oschwald, M., Schik, A., Klar, M. & Mayer, W.1999 Investigation of coaxial LN2/GH2-injection at supercritical pressure by spontaneous Raman scattering. AIAA Paper 99-2887.Google Scholar
Poinsot, T. & Veynantes, D. 2005 Theoretical and Numerical Combustion. R.T. Edwards, Inc., Technology & Engineering.Google Scholar
Poling, B. E., Prausnitz, J. M. & O’Connell, J. P. 2001 The Properties of Gases and Liquids. McGraw-Hill.Google Scholar
Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. 1992 Numerical Recipes in Fortran. Cambridge University Press.Google Scholar
Qiu, L., Wang, Y., Jiao, Q., Wang, H. & Reitz, R. D. 2014 Development of a thermodynamically consistent, robust and efficient phase equilibrium solver and its validations. Fuel 115, 1–16.Google Scholar
Qiu, L. & Reitz, R. D. 2014 Simulation of supercritical fuel injection with condensation. Intl J. Heat Mass Transfer 79, 1070–1086.Google Scholar
Qiu, L. & Reitz, R. D. 2015 An investigation of thermodynamic states during high-pressure fuel injection using equilibrium thermodynamics. Intl J. Multiphase Flow 72, 24–38.Google Scholar
Reitz, R. D. 1988 Modeling atomization processes in high-pressure vaporizing sprays. Atomiz. Sprays 3, 309–337.Google Scholar
Reitz, R. D. & Rutland, C. J. 1995 Development and testing of diesel engine CFD models. Prog. Energy Combust. Sci. 21, 173–196.Google Scholar
Roy, A., Clement Joly, C. & Corin Segal, C. 2013 Disintegrating supercritical jets in a subcritical environment. J. Fluid Mech. 717, 193–202.Google Scholar
Siebers, D. L.1998 Liquid-phase fuel penetration in diesel sprays SAE Paper No. 980809.Google Scholar
Siebers, D. L.1999 Scaling liquid-phase fuel penetration in diesel sprays based on mixing-limited vaporization. SAE Paper No. 1999-01-0528.Google Scholar
Stradi, B. A., Brennecke, J. F., Kohn, P. & Stadtherr, M. A. 2001 Reliable computation of mixture critical points. AIChE J. 47 (1), 212–221.Google Scholar
Taylor, R. & Krishna, R. 1993 Multicomponent Mass Transfer, Wiley Series in Chemical Engineering. Wiley.Google Scholar
Tester, J. W. & Modell, M. 1997 Thermodynamics and its Applications. Prentice Hall PTR.Google Scholar
Wang, Y., Liu, X., Im, K. S., Lee, W. K., Wang, J., Fezzer, K., Hung, D. L. S. & Winkelman, J. R. 2008 Ultrafast X-ray study of dense-liquid-jet flow dynamics using structure-tracking velocimetry. Nat. Phys. 4, 305–309.Google Scholar
Wilke, C. R. 1950 Diffusional properties of multicomponent gases. Chem. Engng Prog. 460 (2), 95–104.Google Scholar
Yu, J. & Eser, S. 1995 Determination of critical properties (T c , P c ) of some jet fuels. Ind. Engng Chem. Res. 34, 404–409.Google Scholar