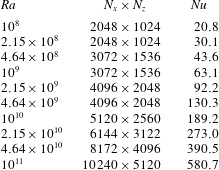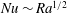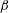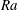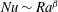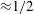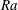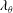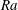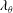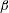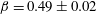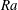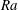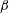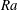1 Introduction
Rayleigh–Bénard (RB) convection (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Lohse & Xia Reference Lohse and Xia2010; Chillà & Schumacher Reference Chillà and Schumacher2012; Xia Reference Xia2013), a flow in a container heated from below and cooled from above, is a paradigmatic system in thermally driven turbulence. The key control parameters are the Rayleigh number and Prandtl number, which are respectively defined as
![]() $Ra=\unicode[STIX]{x1D6FC}g\unicode[STIX]{x1D6E5}L^{3}/(\unicode[STIX]{x1D708}\unicode[STIX]{x1D705})$
and
$Ra=\unicode[STIX]{x1D6FC}g\unicode[STIX]{x1D6E5}L^{3}/(\unicode[STIX]{x1D708}\unicode[STIX]{x1D705})$
and
![]() $Pr=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$
, where
$Pr=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$
, where
![]() $\unicode[STIX]{x1D6FC}$
is the thermal expansion coefficient,
$\unicode[STIX]{x1D6FC}$
is the thermal expansion coefficient,
![]() $g$
the gravitational acceleration,
$g$
the gravitational acceleration,
![]() $\unicode[STIX]{x1D6E5}$
the temperature drop across the container,
$\unicode[STIX]{x1D6E5}$
the temperature drop across the container,
![]() $L$
the height of the fluid domain,
$L$
the height of the fluid domain,
![]() $\unicode[STIX]{x1D708}$
the kinematic viscosity, and
$\unicode[STIX]{x1D708}$
the kinematic viscosity, and
![]() $\unicode[STIX]{x1D705}$
the thermal diffusivity of the fluid. The most relevant response of the system is the heat transfer, which in dimensionless form is expressed as the Nusselt number
$\unicode[STIX]{x1D705}$
the thermal diffusivity of the fluid. The most relevant response of the system is the heat transfer, which in dimensionless form is expressed as the Nusselt number
![]() $Nu$
.
$Nu$
.
Over the years, much attention has been paid to the scaling relation between
![]() $Nu$
and
$Nu$
and
![]() $Ra$
, i.e.
$Ra$
, i.e.
![]() $Nu\sim Ra^{\unicode[STIX]{x1D6FD}}$
. Two of the early attempts were made by Malkus (Reference Malkus1954) and Priestley (Reference Priestley1954), both of whom independently proposed
$Nu\sim Ra^{\unicode[STIX]{x1D6FD}}$
. Two of the early attempts were made by Malkus (Reference Malkus1954) and Priestley (Reference Priestley1954), both of whom independently proposed
![]() $\unicode[STIX]{x1D6FD}=1/3$
, which reflects their assumption that the heat flux is independent of the distance between the two plates and controlled only by the boundary layers (BLs). Grossmann & Lohse (Reference Grossmann and Lohse2000, Reference Grossmann and Lohse2001), based on an analysis and decomposition of the kinetic and thermal energy dissipation rates into bulk and BL contributions, proposed that there are no pure scaling laws but rather a superposition of various ones. For extremely large
$\unicode[STIX]{x1D6FD}=1/3$
, which reflects their assumption that the heat flux is independent of the distance between the two plates and controlled only by the boundary layers (BLs). Grossmann & Lohse (Reference Grossmann and Lohse2000, Reference Grossmann and Lohse2001), based on an analysis and decomposition of the kinetic and thermal energy dissipation rates into bulk and BL contributions, proposed that there are no pure scaling laws but rather a superposition of various ones. For extremely large
![]() $Ra$
, Kraichnan (Reference Kraichnan1962) predicted a so-called ultimate regime with turbulent shear BLs, which led to the relation
$Ra$
, Kraichnan (Reference Kraichnan1962) predicted a so-called ultimate regime with turbulent shear BLs, which led to the relation
![]() $Nu\sim Ra^{1/2}(\ln Ra)^{-3/2}$
, where the logarithmic correction becomes negligible with increasing
$Nu\sim Ra^{1/2}(\ln Ra)^{-3/2}$
, where the logarithmic correction becomes negligible with increasing
![]() $Ra$
(Spiegel Reference Spiegel1963). Yet there are still debates on the various claims of evidence for this regime. With a low-temperature helium RB experiment, Chavanne et al. (Reference Chavanne, Chilla, Castaing, Hebral, Chabaud and Chaussy1997, Reference Chavanne, Chilla, Chabaud, Castaing and Hebral2001) found that
$Ra$
(Spiegel Reference Spiegel1963). Yet there are still debates on the various claims of evidence for this regime. With a low-temperature helium RB experiment, Chavanne et al. (Reference Chavanne, Chilla, Castaing, Hebral, Chabaud and Chaussy1997, Reference Chavanne, Chilla, Chabaud, Castaing and Hebral2001) found that
![]() $\unicode[STIX]{x1D6FD}$
increases to 0.38 for
$\unicode[STIX]{x1D6FD}$
increases to 0.38 for
![]() $Ra=(2\times 10^{11},10^{14})$
. Taking into account the effects of turbulent BLs, Grossmann & Lohse (Reference Grossmann and Lohse2011) derived a scaling law with a different logarithmic correction as compared to Kraichnan (Reference Kraichnan1962) and formulated this relation as an effective power law with a locally determined effective scaling exponent
$Ra=(2\times 10^{11},10^{14})$
. Taking into account the effects of turbulent BLs, Grossmann & Lohse (Reference Grossmann and Lohse2011) derived a scaling law with a different logarithmic correction as compared to Kraichnan (Reference Kraichnan1962) and formulated this relation as an effective power law with a locally determined effective scaling exponent
![]() $\unicode[STIX]{x1D6FD}$
. In particular, they derived that
$\unicode[STIX]{x1D6FD}$
. In particular, they derived that
![]() $\unicode[STIX]{x1D6FD}$
should be approximately 0.38 when
$\unicode[STIX]{x1D6FD}$
should be approximately 0.38 when
![]() $Ra$
is approximately
$Ra$
is approximately
![]() $10^{14}$
. This was demonstrated experimentally by He et al. (Reference He, Funfschilling, Bodenschatz and Ahlers2012a
,Reference He, Funfschilling, Nobach, Bodenschatz and Ahlers
b
). For more information on general aspects of RB convection, we refer the readers to the reviews by Ahlers et al. (Reference Ahlers, Grossmann and Lohse2009), Lohse & Xia (Reference Lohse and Xia2010), Chillà & Schumacher (Reference Chillà and Schumacher2012) and Xia (Reference Xia2013).
$10^{14}$
. This was demonstrated experimentally by He et al. (Reference He, Funfschilling, Bodenschatz and Ahlers2012a
,Reference He, Funfschilling, Nobach, Bodenschatz and Ahlers
b
). For more information on general aspects of RB convection, we refer the readers to the reviews by Ahlers et al. (Reference Ahlers, Grossmann and Lohse2009), Lohse & Xia (Reference Lohse and Xia2010), Chillà & Schumacher (Reference Chillà and Schumacher2012) and Xia (Reference Xia2013).
To avoid the influence of the BLs, and therefore to avoid the logarithmic corrections, several successful model systems have been proposed throughout the years. In numerical experiments with periodic boundary conditions in all directions, Lohse & Toschi (Reference Lohse and Toschi2003) and Calzavarini et al. (Reference Calzavarini, Lohse, Toschi and Tripiccione2005) proposed ‘homogeneous’ RB turbulence; Gibert et al. (Reference Gibert, Pabiou, Chilla and Castaing2006) and Pawar & Arakeri (Reference Pawar and Arakeri2018) performed corresponding RB experiments in a ‘cavity’; Lepot, Aumaître & Gallet (Reference Lepot, Aumaître and Gallet2018) proposed radiative heating convection, in which heat is input directly inside an absorption layer. When this absorption length is thicker than the BLs, radiative heating is allowed to bypass the BLs and heat up the bulk turbulent flow directly. In all these cases a scaling exponent of
![]() $1/2$
was achieved, because the BLs no longer played a role. We call this regime the ‘asymptotic ultimate regime’.
$1/2$
was achieved, because the BLs no longer played a role. We call this regime the ‘asymptotic ultimate regime’.
For conventional RB convection, in which BLs close to the bottom and top plate are formed, wall roughness has been introduced in an attempt to trigger an earlier onset of a turbulent BL; see the reviews Ahlers et al. (Reference Ahlers, Grossmann and Lohse2009), Chillà & Schumacher (Reference Chillà and Schumacher2012) and Xia (Reference Xia2013) for detailed discussions. The results for three-dimensional (3-D) simulations and experiments can be divided into two main categories. First, there are studies which show that roughness can increase the scaling exponent
![]() $\unicode[STIX]{x1D6FD}$
from a value slightly below
$\unicode[STIX]{x1D6FD}$
from a value slightly below
![]() $1/3$
to a value between
$1/3$
to a value between
![]() $1/3$
and
$1/3$
and
![]() $1/2$
(Roche et al.
Reference Roche, Castaing, Chabaud and Hebral2001; Qiu, Xia & Tong Reference Qiu, Xia and Tong2005; Stringano & Verzicco Reference Stringano and Verzicco2006; Tisserand et al.
Reference Tisserand, Creyssels, Gasteuil, Pabiou, Gibert, Castaing and Chilla2011; Salort et al.
Reference Salort, Liot, Rusaouen, Seychelles, Tisserand, Creyssels, Castaing and Chillá2014; Wei et al.
Reference Wei, Chan, Ni, Zhao and Xia2014; Xie & Xia Reference Xie and Xia2017). Shen, Tong & Xia (Reference Shen, Tong and Xia1996), Du & Tong (Reference Du and Tong2000), Wei et al. (Reference Wei, Chan, Ni, Zhao and Xia2014) and Xie & Xia (Reference Xie and Xia2017) found that the scaling exponent
$1/2$
(Roche et al.
Reference Roche, Castaing, Chabaud and Hebral2001; Qiu, Xia & Tong Reference Qiu, Xia and Tong2005; Stringano & Verzicco Reference Stringano and Verzicco2006; Tisserand et al.
Reference Tisserand, Creyssels, Gasteuil, Pabiou, Gibert, Castaing and Chilla2011; Salort et al.
Reference Salort, Liot, Rusaouen, Seychelles, Tisserand, Creyssels, Castaing and Chillá2014; Wei et al.
Reference Wei, Chan, Ni, Zhao and Xia2014; Xie & Xia Reference Xie and Xia2017). Shen, Tong & Xia (Reference Shen, Tong and Xia1996), Du & Tong (Reference Du and Tong2000), Wei et al. (Reference Wei, Chan, Ni, Zhao and Xia2014) and Xie & Xia (Reference Xie and Xia2017) found that the scaling exponent
![]() $\unicode[STIX]{x1D6FD}$
remains roughly the same when roughness is introduced. Whether an increase in the scaling exponent is observed or not depends on the roughness configuration and the explored
$\unicode[STIX]{x1D6FD}$
remains roughly the same when roughness is introduced. Whether an increase in the scaling exponent is observed or not depends on the roughness configuration and the explored
![]() $Ra$
and
$Ra$
and
![]() $Pr$
regime. Roche et al. (Reference Roche, Castaing, Chabaud and Hebral2001) designed the first experiment to possibly reach the ultimate regime without the logarithmic correction (asymptotic ultimate regime) using a cylindrical cell with grooved roughness in both plates and in the sidewall. They observed a scaling exponent
$Pr$
regime. Roche et al. (Reference Roche, Castaing, Chabaud and Hebral2001) designed the first experiment to possibly reach the ultimate regime without the logarithmic correction (asymptotic ultimate regime) using a cylindrical cell with grooved roughness in both plates and in the sidewall. They observed a scaling exponent
![]() $\unicode[STIX]{x1D6FD}$
of 0.51 in the Rayleigh number range
$\unicode[STIX]{x1D6FD}$
of 0.51 in the Rayleigh number range
![]() $Ra=(2\times 10^{12},5\times 10^{13})$
. Wagner & Shishkina (Reference Wagner and Shishkina2015) showed in direct numerical simulations (DNS) for rectangular roughness that the scaling exponent
$Ra=(2\times 10^{12},5\times 10^{13})$
. Wagner & Shishkina (Reference Wagner and Shishkina2015) showed in direct numerical simulations (DNS) for rectangular roughness that the scaling exponent
![]() $\unicode[STIX]{x1D6FD}$
increases compared to the smooth case for low
$\unicode[STIX]{x1D6FD}$
increases compared to the smooth case for low
![]() $Ra$
before it saturates back to the smooth wall value at large
$Ra$
before it saturates back to the smooth wall value at large
![]() $Ra$
. For RB with pyramid-shaped roughness, Xie & Xia (Reference Xie and Xia2017) varied the roughness aspect ratio
$Ra$
. For RB with pyramid-shaped roughness, Xie & Xia (Reference Xie and Xia2017) varied the roughness aspect ratio
![]() $\unicode[STIX]{x1D706}$
, which they define as the height of a roughness element over its base width, from
$\unicode[STIX]{x1D706}$
, which they define as the height of a roughness element over its base width, from
![]() $0.5$
to
$0.5$
to
![]() $4.0$
. With increasing
$4.0$
. With increasing
![]() $Ra$
they identified three regimes. The transition between regime I and II occurs when the thermal BL becomes thinner than the roughness height and the transition between regime II and III occurs when the viscous BL thickness becomes smaller than the roughness height. They found that in regime II the scaling exponent
$Ra$
they identified three regimes. The transition between regime I and II occurs when the thermal BL becomes thinner than the roughness height and the transition between regime II and III occurs when the viscous BL thickness becomes smaller than the roughness height. They found that in regime II the scaling exponent
![]() $\unicode[STIX]{x1D6FD}$
increases from
$\unicode[STIX]{x1D6FD}$
increases from
![]() $0.36$
to
$0.36$
to
![]() $0.59$
when
$0.59$
when
![]() $\unicode[STIX]{x1D706}$
is increased from
$\unicode[STIX]{x1D706}$
is increased from
![]() $0.5$
to
$0.5$
to
![]() $4.0$
. In regime III they found that these scaling exponents saturate to
$4.0$
. In regime III they found that these scaling exponents saturate to
![]() $0.30$
to
$0.30$
to
![]() $0.50$
, respectively, with increasing
$0.50$
, respectively, with increasing
![]() $\unicode[STIX]{x1D706}$
. Rusaouën et al. (Reference Rusaouën, Liot, Castaing, Salort and Chillà2018) performed RB experiments with water in cylindrical containers for
$\unicode[STIX]{x1D706}$
. Rusaouën et al. (Reference Rusaouën, Liot, Castaing, Salort and Chillà2018) performed RB experiments with water in cylindrical containers for
![]() $Ra$
up to
$Ra$
up to
![]() $10^{12}$
. They performed a set of measurements using smooth and rough plates with cubic roughness elements in a square lattice. In these experiments several regimes were identified for the rough case. With increasing
$10^{12}$
. They performed a set of measurements using smooth and rough plates with cubic roughness elements in a square lattice. In these experiments several regimes were identified for the rough case. With increasing
![]() $Ra$
they first observed a regime in which the heat transfer is similar to the smooth case, followed by a regime in which the heat transfer is enhanced by a modification of the
$Ra$
they first observed a regime in which the heat transfer is similar to the smooth case, followed by a regime in which the heat transfer is enhanced by a modification of the
![]() $Nu$
versus
$Nu$
versus
![]() $Ra$
number scaling, before a third regime is obtained in which the heat transfer scaling is similar to the smooth case, but with a larger prefactor.
$Ra$
number scaling, before a third regime is obtained in which the heat transfer scaling is similar to the smooth case, but with a larger prefactor.
For all the rough wall RB studies that we mentioned above, a 3-D geometry of the cell has been adopted. Recently, using DNS of two-dimensional (2-D) RB convection with roughness of varying heights and wavelengths for
![]() $Pr=1$
, Toppaladoddi, Succi & Wettlaufer (Reference Toppaladoddi, Succi and Wettlaufer2017) observed the existence of
$Pr=1$
, Toppaladoddi, Succi & Wettlaufer (Reference Toppaladoddi, Succi and Wettlaufer2017) observed the existence of
![]() $\unicode[STIX]{x1D6FD}=0.483$
by fitting the data in the range
$\unicode[STIX]{x1D6FD}=0.483$
by fitting the data in the range
![]() $Ra=(4.6\times 10^{6},3\times 10^{9})$
and interpreted this exponent as an achievement of the ultimate regime. In contrast, Zhu et al. (Reference Zhu, Stevens, Verzicco and Lohse2017) showed that: (i) there is no pure scaling exponent in that
$Ra=(4.6\times 10^{6},3\times 10^{9})$
and interpreted this exponent as an achievement of the ultimate regime. In contrast, Zhu et al. (Reference Zhu, Stevens, Verzicco and Lohse2017) showed that: (i) there is no pure scaling exponent in that
![]() $Ra$
range; (ii) although
$Ra$
range; (ii) although
![]() $\unicode[STIX]{x1D6FD}$
can locally reach
$\unicode[STIX]{x1D6FD}$
can locally reach
![]() $1/2$
in the range
$1/2$
in the range
![]() $Ra=(10^{8},3\times 10^{9})$
, this should not be interpreted as the attainment of the ultimate regime, because a further increase of
$Ra=(10^{8},3\times 10^{9})$
, this should not be interpreted as the attainment of the ultimate regime, because a further increase of
![]() $Ra$
leads to another regime where a thin thermal BL uniformly follows the rough surfaces, and thus the classical BL-controlled regime is recovered, causing the scaling to saturate to the classical effective
$Ra$
leads to another regime where a thin thermal BL uniformly follows the rough surfaces, and thus the classical BL-controlled regime is recovered, causing the scaling to saturate to the classical effective
![]() $Nu$
versus
$Nu$
versus
![]() $Ra$
scaling exponent close to
$Ra$
scaling exponent close to
![]() $1/3$
.
$1/3$
.
The main question we want to address in this paper is: can the range of
![]() $Ra$
where the effective
$Ra$
where the effective
![]() $1/2$
scaling exponent manifests be extended? We note that in all the studies mentioned above, uniform roughness of a single length scale was adopted. For this situation, the
$1/2$
scaling exponent manifests be extended? We note that in all the studies mentioned above, uniform roughness of a single length scale was adopted. For this situation, the
![]() $1/2$
effective exponent can be observed when roughness starts to perturb the thermal BL, as mentioned before. If, with increasing
$1/2$
effective exponent can be observed when roughness starts to perturb the thermal BL, as mentioned before. If, with increasing
![]() $Ra$
, smaller and smaller roughness length scales are introduced, the different size roughness elements will protrude through the thermal BL one by one. Therefore, the flow can be maintained in a transition state and the
$Ra$
, smaller and smaller roughness length scales are introduced, the different size roughness elements will protrude through the thermal BL one by one. Therefore, the flow can be maintained in a transition state and the
![]() $1/2$
effective exponent can be sustained. In this manuscript, we will demonstrate this conjecture by means of multiscale wall roughness. In fact, two decades ago Villermaux (Reference Villermaux1998) theoretically pioneered the research of RB convection with multiscale cubic roughness, with power-law-distributed asperity heights. He formulated a new scaling relation and found that the heat transfer scaling exponent can be significantly enhanced. Later, Ciliberto & Laroche (Reference Ciliberto and Laroche1999) experimentally explored multiscale roughness by gluing glass spheres of controlled diameter on the bottom copper plate, and found that
$1/2$
effective exponent can be sustained. In this manuscript, we will demonstrate this conjecture by means of multiscale wall roughness. In fact, two decades ago Villermaux (Reference Villermaux1998) theoretically pioneered the research of RB convection with multiscale cubic roughness, with power-law-distributed asperity heights. He formulated a new scaling relation and found that the heat transfer scaling exponent can be significantly enhanced. Later, Ciliberto & Laroche (Reference Ciliberto and Laroche1999) experimentally explored multiscale roughness by gluing glass spheres of controlled diameter on the bottom copper plate, and found that
![]() $\unicode[STIX]{x1D6FD}$
increases to 0.45. In contrast, for a periodic roughness case, they found that the scaling exponent is similar to that in the smooth case.
$\unicode[STIX]{x1D6FD}$
increases to 0.45. In contrast, for a periodic roughness case, they found that the scaling exponent is similar to that in the smooth case.
Another motivation for this study is that for real-world applications and geophysical flows, the situation is far more complex, with surface roughness often containing different length scales. For example, in cities, there is huge difference among the heights of the buildings, and also natural terrains contain multiscale structure. Assuming roughness is multiscale provides a practically useful simplification (Rodriguez-Iturbe et al. Reference Rodriguez-Iturbe, Marani, Rigon and Rinaldo1994).
The paper is organized as follows: in § 2 we describe the numerical method and the parameter set-up used in the simulations. In § 3 we show how multiscale roughness alters RB turbulence. In § 4 we briefly summarize the results and give an outlook to potential future work.
2 Numerical details
We solve the Boussinesq equations with the second-order staggered finite-difference code AFiD (Verzicco & Orlandi Reference Verzicco and Orlandi1996; van der Poel et al.
Reference van der Poel, Ostilla-Mónico, Donners and Verzicco2015; Zhu et al.
Reference Zhu, Phillips, Spandan, Donners, Ruetsch, Romero, Ostilla-Mónico, Yang, Lohse, Verzicco, Massimiliano and Stevens2018b
) in 2-D. The reason why we resorted to 2-D simulations is that they are much less expensive than the 3-D case and thus we can cover a much wider range of
![]() $Ra$
. The details of the numerical methods, the parallelization and the different versions (CPU and GPU) can be found in Verzicco & Orlandi (Reference Verzicco and Orlandi1996), van der Poel et al. (Reference van der Poel, Ostilla-Mónico, Donners and Verzicco2015) and Zhu et al. (Reference Zhu, Phillips, Spandan, Donners, Ruetsch, Romero, Ostilla-Mónico, Yang, Lohse, Verzicco, Massimiliano and Stevens2018b
). The code has been extensively validated and used under various conditions (Zhu et al.
Reference Zhu, Stevens, Verzicco and Lohse2017, Reference Zhu, Mathai, Stevens, Verzicco and Lohse2018a
,Reference Zhu, Phillips, Spandan, Donners, Ruetsch, Romero, Ostilla-Mónico, Yang, Lohse, Verzicco, Massimiliano and Stevens
b
). The governing equations in the dimensionless form read:
$Ra$
. The details of the numerical methods, the parallelization and the different versions (CPU and GPU) can be found in Verzicco & Orlandi (Reference Verzicco and Orlandi1996), van der Poel et al. (Reference van der Poel, Ostilla-Mónico, Donners and Verzicco2015) and Zhu et al. (Reference Zhu, Phillips, Spandan, Donners, Ruetsch, Romero, Ostilla-Mónico, Yang, Lohse, Verzicco, Massimiliano and Stevens2018b
). The code has been extensively validated and used under various conditions (Zhu et al.
Reference Zhu, Stevens, Verzicco and Lohse2017, Reference Zhu, Mathai, Stevens, Verzicco and Lohse2018a
,Reference Zhu, Phillips, Spandan, Donners, Ruetsch, Romero, Ostilla-Mónico, Yang, Lohse, Verzicco, Massimiliano and Stevens
b
). The governing equations in the dimensionless form read:
where
![]() $\hat{\boldsymbol{z}}$
is the unit vector pointing in the direction opposite to gravity,
$\hat{\boldsymbol{z}}$
is the unit vector pointing in the direction opposite to gravity,
![]() $\boldsymbol{u}$
the velocity vector normalized by the free-fall velocity
$\boldsymbol{u}$
the velocity vector normalized by the free-fall velocity
![]() $\sqrt{g\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5}L}$
,
$\sqrt{g\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5}L}$
,
![]() $t$
the dimensionless time normalized by
$t$
the dimensionless time normalized by
![]() $\sqrt{L/(g\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5})}$
,
$\sqrt{L/(g\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5})}$
,
![]() $\unicode[STIX]{x1D703}$
the temperature normalized by
$\unicode[STIX]{x1D703}$
the temperature normalized by
![]() $\unicode[STIX]{x1D6E5}$
, and
$\unicode[STIX]{x1D6E5}$
, and
![]() $p$
the pressure normalized by
$p$
the pressure normalized by
![]() $g\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5}/L$
. As shown in the above equations, the control parameters of the system are
$g\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5}/L$
. As shown in the above equations, the control parameters of the system are
![]() $Ra$
and
$Ra$
and
![]() $Pr$
. The boundary conditions on the top and bottom plates are no-slip for the velocity and constant for the temperature. Periodic conditions are applied to the horizontal boundaries. In all our simulations,
$Pr$
. The boundary conditions on the top and bottom plates are no-slip for the velocity and constant for the temperature. Periodic conditions are applied to the horizontal boundaries. In all our simulations,
![]() $Pr$
is fixed to 1. The aspect ratio is chosen as
$Pr$
is fixed to 1. The aspect ratio is chosen as
![]() $\unicode[STIX]{x1D6E4}\equiv W/L=2$
, where
$\unicode[STIX]{x1D6E4}\equiv W/L=2$
, where
![]() $W$
is the width of the computational domain.
$W$
is the width of the computational domain.
For the rough cases, the characteristic length scale that we use to express
![]() $Ra$
is the equivalent smooth wall height
$Ra$
is the equivalent smooth wall height
![]() $L^{\prime }$
. This height is defined by determining the height of a domain with smooth boundaries that would have the same fluid volume.
$L^{\prime }$
. This height is defined by determining the height of a domain with smooth boundaries that would have the same fluid volume.
![]() $Nu$
is calculated from
$Nu$
is calculated from
![]() $Nu=\sqrt{RaPr}\langle u_{z}\unicode[STIX]{x1D703}\rangle _{A}-\langle \unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D703}\rangle _{A}$
, where
$Nu=\sqrt{RaPr}\langle u_{z}\unicode[STIX]{x1D703}\rangle _{A}-\langle \unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D703}\rangle _{A}$
, where
![]() $u_{z}$
denotes the instantaneous vertical velocity and
$u_{z}$
denotes the instantaneous vertical velocity and
![]() $\langle \cdot \rangle _{A}$
the average over any horizontal plane between the rough plates.
$\langle \cdot \rangle _{A}$
the average over any horizontal plane between the rough plates.

Figure 1. (a) A sketch of the computational domain and the roughness elements. (b) Roughness element
![]() $R_{1}$
is the base element and the length scale is
$R_{1}$
is the base element and the length scale is
![]() $R_{1}=0.1$
. The structure is multiscale as
$R_{1}=0.1$
. The structure is multiscale as
![]() $R_{n+1}=2^{-n}R_{n}$
,
$R_{n+1}=2^{-n}R_{n}$
,
![]() $n=1,2,3$
.
$n=1,2,3$
.
An immersed boundary method (IBM) has been implemented to cope with rough surfaces (Fadlun et al. Reference Fadlun, Verzicco, Orlandi and Mohd-Yusof2000). The basic idea of the IBM is that a body force term in the Navier–Stokes equation can mimic the effects of the boundaries. For more information on IBM, we refer to the reviews by Peskin (Reference Peskin2002) and Mittal & Iaccarino (Reference Mittal and Iaccarino2005).
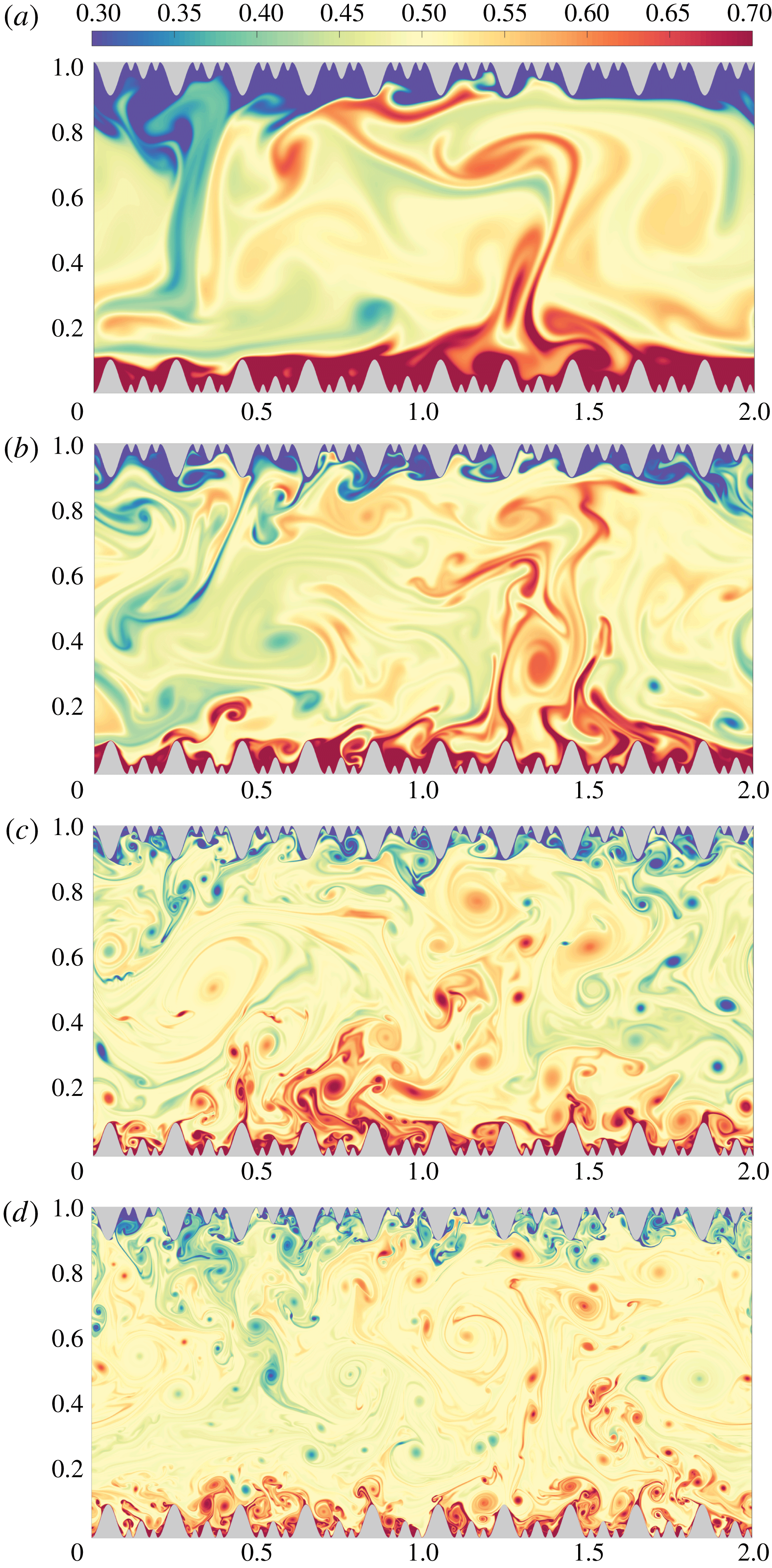
Figure 2. The instantaneous temperature fields at (a)
![]() $Ra=10^{8}$
, (b)
$Ra=10^{8}$
, (b)
![]() $Ra=10^{9}$
, (c)
$Ra=10^{9}$
, (c)
![]() $Ra=10^{10}$
and (d)
$Ra=10^{10}$
and (d)
![]() $Ra=10^{11}$
. It can be seen that with
$Ra=10^{11}$
. It can be seen that with
![]() $Ra$
increasing, plumes are ejected also from smaller and smaller roughness elements.
$Ra$
increasing, plumes are ejected also from smaller and smaller roughness elements.
We now describe the multiscale roughness pattern: we choose a series of wall-mounted sinusoidal elements distributed on both the top and bottom plates. The sinusoidal elements all have the same aspect ratio 1. The multiscale roughness implementation is similar to that in Yang & Meneveau (Reference Yang and Meneveau2017), although in that study square roughness elements were adopted and positioned randomly. The size of the largest roughness element is used as the reference scale,
![]() $R_{1}=0.1$
. At the second and third generation, we have the rough elements size as
$R_{1}=0.1$
. At the second and third generation, we have the rough elements size as
![]() $R_{n+1}=2^{-n}R_{n}$
. No roughness elements of intermediate sizes are included, and the roughness height spectrum is thus discrete (Yang & Meneveau Reference Yang and Meneveau2017). Figure 1 gives an overview of the computational domain and the roughness elements. Adequate resolution was ensured for all cases, i.e. the mesh is stretched in the wall normal direction with the finest grid implemented around the tips of the biggest roughness elements. There are at least 12 points inside the BL. The statistics were averaged over 200 free-fall time units. In the rough case for
$R_{n+1}=2^{-n}R_{n}$
. No roughness elements of intermediate sizes are included, and the roughness height spectrum is thus discrete (Yang & Meneveau Reference Yang and Meneveau2017). Figure 1 gives an overview of the computational domain and the roughness elements. Adequate resolution was ensured for all cases, i.e. the mesh is stretched in the wall normal direction with the finest grid implemented around the tips of the biggest roughness elements. There are at least 12 points inside the BL. The statistics were averaged over 200 free-fall time units. In the rough case for
![]() $Ra=10^{11}$
,
$Ra=10^{11}$
,
![]() $10\,240\times 5120$
grid points, in the horizontal and vertical direction, respectively, were used. Further details about the simulation parameters can be found in appendix A.
$10\,240\times 5120$
grid points, in the horizontal and vertical direction, respectively, were used. Further details about the simulation parameters can be found in appendix A.
3 Results
We first compare the flow structures for increasing
![]() $Ra$
. Figure 2 shows the instantaneous temperature snapshots for four
$Ra$
. Figure 2 shows the instantaneous temperature snapshots for four
![]() $Ra$
, ranging from
$Ra$
, ranging from
![]() $10^{8}$
to
$10^{8}$
to
![]() $10^{11}$
. At the lowest
$10^{11}$
. At the lowest
![]() $Ra=10^{8}$
, within the cavity regions, the flow is viscosity dominated. Interestingly, figure 3 shows that the heat transfer for the case with multiscale roughness is approximately
$Ra=10^{8}$
, within the cavity regions, the flow is viscosity dominated. Interestingly, figure 3 shows that the heat transfer for the case with multiscale roughness is approximately
![]() $15\,\%$
lower than for the case with smooth walls. The same phenomenon of heat transfer reduction due to roughness was observed by Shishkina & Wagner (Reference Shishkina and Wagner2011) and Zhang et al. (Reference Zhang, Sun, Bao and Zhou2018). The physical reason for the heat transfer reduction is that the hot/cold fluid is trapped between the roughness elements, which thus leads to a thicker thermal BL and therefore to a lower overall heat transport. For larger
$15\,\%$
lower than for the case with smooth walls. The same phenomenon of heat transfer reduction due to roughness was observed by Shishkina & Wagner (Reference Shishkina and Wagner2011) and Zhang et al. (Reference Zhang, Sun, Bao and Zhou2018). The physical reason for the heat transfer reduction is that the hot/cold fluid is trapped between the roughness elements, which thus leads to a thicker thermal BL and therefore to a lower overall heat transport. For larger
![]() $Ra$
, plumes start to develop from the tips of the roughness elements and eventually, at the largest
$Ra$
, plumes start to develop from the tips of the roughness elements and eventually, at the largest
![]() $Ra=10^{11}$
, plumes are formed even in the sloping surfaces of the smallest rough elements. This observation indicates the impact of multiscale roughness on the flow structure and heat transfer for increasing
$Ra=10^{11}$
, plumes are formed even in the sloping surfaces of the smallest rough elements. This observation indicates the impact of multiscale roughness on the flow structure and heat transfer for increasing
![]() $Ra$
.
$Ra$
.
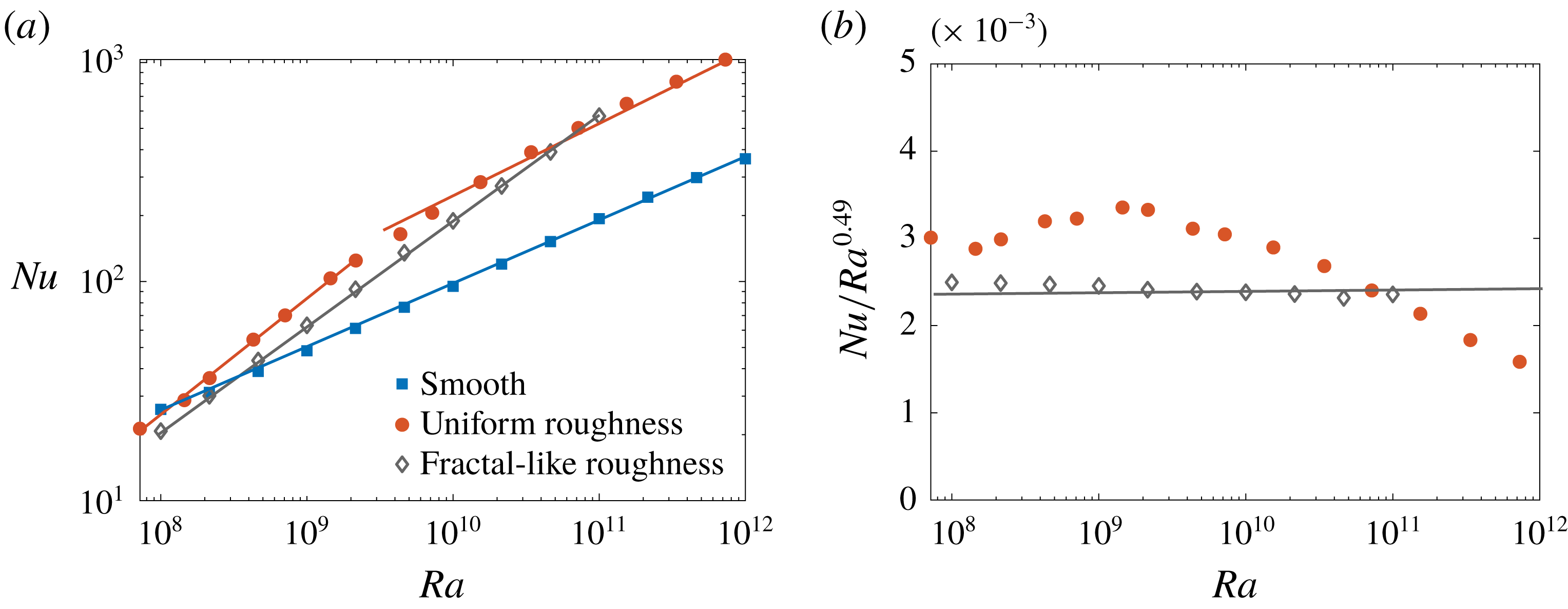
Figure 3. (a)
![]() $Nu$
as a function
$Nu$
as a function
![]() $Ra$
for the smooth case and the multiscale rough case. For the smooth case, the scaling exponent is
$Ra$
for the smooth case and the multiscale rough case. For the smooth case, the scaling exponent is
![]() $\unicode[STIX]{x1D6FD}=0.29\pm 0.01$
. For the multiscale rough case, the scaling exponent is
$\unicode[STIX]{x1D6FD}=0.29\pm 0.01$
. For the multiscale rough case, the scaling exponent is
![]() $\unicode[STIX]{x1D6FD}=0.49\pm 0.02$
. As a reference, the results for mono-scale roughness are also included (Zhu et al.
Reference Zhu, Stevens, Verzicco and Lohse2017), which clearly show two scaling regimes. Note that
$\unicode[STIX]{x1D6FD}=0.49\pm 0.02$
. As a reference, the results for mono-scale roughness are also included (Zhu et al.
Reference Zhu, Stevens, Verzicco and Lohse2017), which clearly show two scaling regimes. Note that
![]() $Ra$
is defined based on the equivalent smooth wall height. In the mono-scale roughness case, 20 sinusoidal roughness elements of the same height (0.1) were adopted. For the multiscale roughness cases considered here, 10 of these large roughness elements are replaced by one
$Ra$
is defined based on the equivalent smooth wall height. In the mono-scale roughness case, 20 sinusoidal roughness elements of the same height (0.1) were adopted. For the multiscale roughness cases considered here, 10 of these large roughness elements are replaced by one
![]() $R_{2}$
and two
$R_{2}$
and two
![]() $R_{3}$
generation roughness elements. Therefore, the total number of roughness elements for the multiscale roughness geometry is
$R_{3}$
generation roughness elements. Therefore, the total number of roughness elements for the multiscale roughness geometry is
![]() $40$
.
$40$
.
![]() $Nu$
is smaller for the multiscale roughness case than for the mono-scale roughness case, because the latter has larger roughness elements. (b) Same as in (a) but in a compensated way for the multiscale rough case. Note that we use only one specific aspect ratio for the roughness elements. If the aspect ratio changes, the scaling exponent will also change.
$Nu$
is smaller for the multiscale roughness case than for the mono-scale roughness case, because the latter has larger roughness elements. (b) Same as in (a) but in a compensated way for the multiscale rough case. Note that we use only one specific aspect ratio for the roughness elements. If the aspect ratio changes, the scaling exponent will also change.

Figure 4. Sketches on why regular periodic roughness with the same height leads to scaling saturation and why multiscale roughness increases the exponent in a wider range of
![]() $Ra$
. Orange parts are the regions where the thermal BL are. (a) At lower
$Ra$
. Orange parts are the regions where the thermal BL are. (a) At lower
![]() $Ra$
, the roughness is below the thermal BL and has little impact on scaling relations. (b,c) At intermediate
$Ra$
, the roughness is below the thermal BL and has little impact on scaling relations. (b,c) At intermediate
![]() $Ra$
, the roughness starts to protrude through the thermal BL, but not to the valley of the roughness elements. For multiscale roughness, it is easy to imagine that the range of
$Ra$
, the roughness starts to protrude through the thermal BL, but not to the valley of the roughness elements. For multiscale roughness, it is easy to imagine that the range of
![]() $Ra$
is wider in this stage, as only with increasing
$Ra$
is wider in this stage, as only with increasing
![]() $Ra$
will the smaller and smaller roughness elements protrude through the thermal BL. (d) When Ra is large enough, a thin thermal BL is uniformly distributed along the rough surfaces and the scaling exponent will saturate back to the value close to the smooth case. This case is not reached in this study.
$Ra$
will the smaller and smaller roughness elements protrude through the thermal BL. (d) When Ra is large enough, a thin thermal BL is uniformly distributed along the rough surfaces and the scaling exponent will saturate back to the value close to the smooth case. This case is not reached in this study.
Next, we check how the scaling relation evolves with increasing
![]() $Ra$
, comparing the smooth and the multiscale case. Figure 3 shows the
$Ra$
, comparing the smooth and the multiscale case. Figure 3 shows the
![]() $Nu$
scaling behaviour as a function of
$Nu$
scaling behaviour as a function of
![]() $Ra$
, in a log–log plot and in a compensated plot. As was shown before in 2-D RB (DeLuca et al.
Reference Deluca, Werne, Rosner and Cattaneo1990; Johnston & Doering Reference Johnston and Doering2009; Zhu et al.
Reference Zhu, Stevens, Verzicco and Lohse2017), the smooth case has an effective scaling exponent
$Ra$
, in a log–log plot and in a compensated plot. As was shown before in 2-D RB (DeLuca et al.
Reference Deluca, Werne, Rosner and Cattaneo1990; Johnston & Doering Reference Johnston and Doering2009; Zhu et al.
Reference Zhu, Stevens, Verzicco and Lohse2017), the smooth case has an effective scaling exponent
![]() $\unicode[STIX]{x1D6FD}=0.29\pm 0.01$
, extending over four decades, from
$\unicode[STIX]{x1D6FD}=0.29\pm 0.01$
, extending over four decades, from
![]() $Ra=10^{8}$
to
$Ra=10^{8}$
to
![]() $Ra=10^{12}$
. For the mono-scale roughness case, two distinct effective scaling exponent can be observed, i.e.
$Ra=10^{12}$
. For the mono-scale roughness case, two distinct effective scaling exponent can be observed, i.e.
![]() $\unicode[STIX]{x1D6FD}=0.50\pm 0.02$
, for one and half decade; then
$\unicode[STIX]{x1D6FD}=0.50\pm 0.02$
, for one and half decade; then
![]() $\unicode[STIX]{x1D6FD}$
saturates back to 0.33. With the introduction of multiscale roughness, the heat transfer is greatly enhanced. Within 95 % of the confidence bound, we get the fit of
$\unicode[STIX]{x1D6FD}$
saturates back to 0.33. With the introduction of multiscale roughness, the heat transfer is greatly enhanced. Within 95 % of the confidence bound, we get the fit of
![]() $Nu\sim 0.00257Ra^{0.49\pm 0.02}$
for three decades of
$Nu\sim 0.00257Ra^{0.49\pm 0.02}$
for three decades of
![]() $Ra$
, from
$Ra$
, from
![]() $Ra=10^{8}$
to
$Ra=10^{8}$
to
![]() $Ra=10^{11}$
. A root mean square error 2.89 is found for the fit. To our knowledge, this is the first realization of such a large scaling exponent in such a wide range of
$Ra=10^{11}$
. A root mean square error 2.89 is found for the fit. To our knowledge, this is the first realization of such a large scaling exponent in such a wide range of
![]() $Ra$
in RB. It is remarkable that it is realized in spite of the relatively low
$Ra$
in RB. It is remarkable that it is realized in spite of the relatively low
![]() $Ra$
numbers of the simulations. Obviously, as for the smooth RB, an asymptotic
$Ra$
numbers of the simulations. Obviously, as for the smooth RB, an asymptotic
![]() $1/2$
exponent is expected only when
$1/2$
exponent is expected only when
![]() $Ra$
approaches infinity.
$Ra$
approaches infinity.
We will now explain the physical mechanism which leads to this considerable enhancement of the exponent for a wide range of
![]() $Ra$
. Let us first recall why in the case of periodic roughness with one single height, the regime with an effective scaling exponent close to
$Ra$
. Let us first recall why in the case of periodic roughness with one single height, the regime with an effective scaling exponent close to
![]() $1/2$
survives for a limited range of
$1/2$
survives for a limited range of
![]() $Ra$
and then saturates back to a value close to the smooth case. In the former regime, the roughness elements start to protrude into the thermal BL. Only weak secondary vortices are generated in the cavities and the resulting mixing is not efficient. Therefore, the flow there is still dominated by viscosity. In the latter regime, secondary vortices are strong enough to mix all the fluids inside the cavities. Thus the roughness elements are covered by a thin thermal BL which is uniformly distributed along the rough surfaces, effectively mimicking an increased wet surface area. Therefore, the effect of BL is restored and the classical BL-controlled regime is retrieved (Zhu et al.
Reference Zhu, Stevens, Verzicco and Lohse2017).
$Ra$
and then saturates back to a value close to the smooth case. In the former regime, the roughness elements start to protrude into the thermal BL. Only weak secondary vortices are generated in the cavities and the resulting mixing is not efficient. Therefore, the flow there is still dominated by viscosity. In the latter regime, secondary vortices are strong enough to mix all the fluids inside the cavities. Thus the roughness elements are covered by a thin thermal BL which is uniformly distributed along the rough surfaces, effectively mimicking an increased wet surface area. Therefore, the effect of BL is restored and the classical BL-controlled regime is retrieved (Zhu et al.
Reference Zhu, Stevens, Verzicco and Lohse2017).
Multiscale roughness essentially extends this effective
![]() $1/2$
scaling regime further. Figure 4 shows sketches of thermal BLs for increasing
$1/2$
scaling regime further. Figure 4 shows sketches of thermal BLs for increasing
![]() $Ra$
. As
$Ra$
. As
![]() $Ra$
increases, the thermal BL becomes thinner, the smaller roughness elements start to perturb the thermal BL, and this process continues until the smallest roughness elements perturb the thermal BL. Therefore, the system stays in the transitioning state and the
$Ra$
increases, the thermal BL becomes thinner, the smaller roughness elements start to perturb the thermal BL, and this process continues until the smallest roughness elements perturb the thermal BL. Therefore, the system stays in the transitioning state and the
![]() $1/2$
exponent is observed over a wider range of
$1/2$
exponent is observed over a wider range of
![]() $Ra$
, compared to the case of periodic roughness with the same height. To give further evidence for this explanation, in figure 5, we show the averaged mean temperature profiles for the valley points in the cavity regions of the roughness elements close to the wall. From the temperature profile for
$Ra$
, compared to the case of periodic roughness with the same height. To give further evidence for this explanation, in figure 5, we show the averaged mean temperature profiles for the valley points in the cavity regions of the roughness elements close to the wall. From the temperature profile for
![]() $Ra=10^{8}$
we can detect the influence of the largest roughness
$Ra=10^{8}$
we can detect the influence of the largest roughness
![]() $R_{1}$
. At
$R_{1}$
. At
![]() $Ra=10^{9}$
also the effect of the
$Ra=10^{9}$
also the effect of the
![]() $R_{2}$
roughness can be identified. Last, but not least, at
$R_{2}$
roughness can be identified. Last, but not least, at
![]() $Ra=10^{10}$
, the influence of smallest
$Ra=10^{10}$
, the influence of smallest
![]() $R_{3}$
roughness starts to manifest.
$R_{3}$
roughness starts to manifest.

Figure 5. Mean temperature profile as a function of the wall normal coordinate averaged at the
![]() $x$
-locations of the valley points in the cavity regions, i.e. the locations where no roughness is added on top of the plate. As explained in the caption of figure 1 there are 40 roughness elements, and these profiles are averaged over all 40 corresponding valley locations.
$x$
-locations of the valley points in the cavity regions, i.e. the locations where no roughness is added on top of the plate. As explained in the caption of figure 1 there are 40 roughness elements, and these profiles are averaged over all 40 corresponding valley locations.
4 Summary, discussion, and outlook
In this manuscript, we use 2-D DNS to study the effects of multiscale roughness on RB turbulence. In our case, the multiscale roughness is composed of three different roughness length scales of sinusoidal shapes. We show that with this implementation the
![]() $Nu$
versus
$Nu$
versus
![]() $Ra$
scaling relation
$Ra$
scaling relation
![]() $Nu\sim Ra^{0.49\pm 0.02}$
can be observed for at least three decades of
$Nu\sim Ra^{0.49\pm 0.02}$
can be observed for at least three decades of
![]() $Ra$
, while for mono-scale roughness the scaling could be observed only for only one and half decades in
$Ra$
, while for mono-scale roughness the scaling could be observed only for only one and half decades in
![]() $Ra$
(Zhu et al.
Reference Zhu, Stevens, Verzicco and Lohse2017). However, there are still several open issues, for example:
$Ra$
(Zhu et al.
Reference Zhu, Stevens, Verzicco and Lohse2017). However, there are still several open issues, for example:
(i) We stress that even though we found
 $Nu\sim Ra^{0.5}$
over an extended
$Nu\sim Ra^{0.5}$
over an extended
 $Ra$
range, this is probably still a transitional regime and not the (asymptotic) ultimate regime in which the BLs are fully turbulent. This means that it is very likely that for the considered roughness geometry the heat transfer scaling exponent saturates back to the value of the smooth case for larger
$Ra$
range, this is probably still a transitional regime and not the (asymptotic) ultimate regime in which the BLs are fully turbulent. This means that it is very likely that for the considered roughness geometry the heat transfer scaling exponent saturates back to the value of the smooth case for larger
 $Ra$
. The situation may also change once the BL become turbulent. Recently, MacDonald et al. (Reference MacDonald, Hutchins, Lohse and Chung2019) found an effective exponent of
$Ra$
. The situation may also change once the BL become turbulent. Recently, MacDonald et al. (Reference MacDonald, Hutchins, Lohse and Chung2019) found an effective exponent of
 $\unicode[STIX]{x1D6FD}\approx 0.42$
in the large-
$\unicode[STIX]{x1D6FD}\approx 0.42$
in the large-
 $Ra$
regime for forced convection in channel flow under the assumption that the BL profile become logarithmic.
$Ra$
regime for forced convection in channel flow under the assumption that the BL profile become logarithmic.(ii) In this work, we modelled three different roughness length scales. We expect that with more length scales, the
 $Ra$
range in which the
$Ra$
range in which the
 $1/2$
scaling exponent manifests might be more extended. Simulations for RB with more roughness length scales are needed to settle this question.
$1/2$
scaling exponent manifests might be more extended. Simulations for RB with more roughness length scales are needed to settle this question.(iii) The current simulations are for 2-D only and it would be interesting to see results in a fully 3-D case. Such simulations would be much more computationally intensive, but very interesting comparisons to the experimental results by, for example, Roche et al. (Reference Roche, Castaing, Chabaud and Hebral2001) would be possible. In that study a scaling exponent of approximately
 $1/2$
up to approximately
$1/2$
up to approximately
 $Ra=5\times 10^{13}$
was observed.
$Ra=5\times 10^{13}$
was observed.(iv) Ciliberto & Laroche (Reference Ciliberto and Laroche1999) observed
 $\unicode[STIX]{x1D6FD}\approx 0.45$
for RB with multiscale glass spheres glued on a copper plate. Understanding the effect of the different heat conductivities for the two roughness elements (glue and glass, both with smaller heat conductivity than copper) will be very helpful.
$\unicode[STIX]{x1D6FD}\approx 0.45$
for RB with multiscale glass spheres glued on a copper plate. Understanding the effect of the different heat conductivities for the two roughness elements (glue and glass, both with smaller heat conductivity than copper) will be very helpful.(v) Here we consider only the situation for
 $Pr=1$
. Recent experiments by Xie & Xia (Reference Xie and Xia2017) suggest that also the
$Pr=1$
. Recent experiments by Xie & Xia (Reference Xie and Xia2017) suggest that also the
 $Pr$
number might play an important role on the effect of roughness on the overall heat transport. Simulations to investigate this effect would be very interesting.
$Pr$
number might play an important role on the effect of roughness on the overall heat transport. Simulations to investigate this effect would be very interesting.(vi) Finally we note that for turbulent Taylor–Couette flow with mono-scale roughness that aligns in the azimuthal direction, simulations (Zhu et al. Reference Zhu, Ostilla-Monico, Verzicco and Lohse2016) yielded an intermediate regime where ‘Nusselt number’
 $Nu_{\unicode[STIX]{x1D714}}\sim Ta^{0.5}$
(angular velocity transport versus Taylor number). When
$Nu_{\unicode[STIX]{x1D714}}\sim Ta^{0.5}$
(angular velocity transport versus Taylor number). When
 $Ta$
is large enough, the exponent saturates back to the smooth case value. The question is whether the
$Ta$
is large enough, the exponent saturates back to the smooth case value. The question is whether the
 $Ta$
range where the
$Ta$
range where the
 $1/2$
exponent shows up can also be extended with multiscale roughness. For turbulent Taylor–Couette flow with mono-scale roughness that aligns in the axial direction, the asymptotic ultimate regime
$1/2$
exponent shows up can also be extended with multiscale roughness. For turbulent Taylor–Couette flow with mono-scale roughness that aligns in the axial direction, the asymptotic ultimate regime
 $1/2$
scaling has already been achieved (Cadot et al.
Reference Cadot, Couder, Daerr, Douady and Tsinober1997; van den Berg et al.
Reference van den Berg, Doering, Lohse and Lathrop2003; Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018c
), and pressure drag has been identified as the origin thereof (Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018c
).
$1/2$
scaling has already been achieved (Cadot et al.
Reference Cadot, Couder, Daerr, Douady and Tsinober1997; van den Berg et al.
Reference van den Berg, Doering, Lohse and Lathrop2003; Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018c
), and pressure drag has been identified as the origin thereof (Zhu et al.
Reference Zhu, Verschoof, Bakhuis, Huisman, Verzicco, Sun and Lohse2018c
).
Acknowledgements
This work was financially supported by the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation programme (grant agreement no. 740479) and the Netherlands Center for Multiscale Catalytic Energy Conversion (MCEC), an NWO Gravitation programme funded by the Ministry of Education, Culture and Science of the Government of the Netherlands. We acknowledge support by the Priority Program SPP 1881 ‘Turbulent Superstructures’ of the Deutsche Forschungsgemeinschaft (DFG). This work was partially carried out on the Dutch national e-infrastructure with the support of SURF Cooperative. We also acknowledge PRACE for awarding us access to MareNostrum based in Italy at the Barcelona Supercomputing Center (BSC) and JUWELS at the Jülich Supercomputing Centre under PRACE project number 2017174146.
Appendix. Numerical details
The numerical details are given in table 1.
Table 1.
![]() $Ra$
, resolution in the horizontal (
$Ra$
, resolution in the horizontal (
![]() $n_{x}$
) and wall normal (
$n_{x}$
) and wall normal (
![]() $n_{z}$
) directions, and
$n_{z}$
) directions, and
![]() $Nu$
number for the multiscale roughness cases considered in this study. For all cases the domain aspect ratio is 2 and
$Nu$
number for the multiscale roughness cases considered in this study. For all cases the domain aspect ratio is 2 and
![]() $Pr=1$
. The uncertainties in
$Pr=1$
. The uncertainties in
![]() $Nu$
is smaller than
$Nu$
is smaller than
![]() $1\,\%$
for all cases. Corresponding information for the mono-scale roughness cases has been reported in Zhu et al. (Reference Zhu, Stevens, Verzicco and Lohse2017) and for the smooth case in Zhu et al. (Reference Zhu, Mathai, Stevens, Verzicco and Lohse2018a
).
$1\,\%$
for all cases. Corresponding information for the mono-scale roughness cases has been reported in Zhu et al. (Reference Zhu, Stevens, Verzicco and Lohse2017) and for the smooth case in Zhu et al. (Reference Zhu, Mathai, Stevens, Verzicco and Lohse2018a
).