Hostname: page-component-7479d7b7d-wxhwt Total loading time: 0 Render date: 2024-07-10T23:29:29.113Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical solutions of compressible convection with an infinite Prandtl number: comparison of the anelastic and anelastic liquid models with the exact equations

Published online by Cambridge University Press:  26 June 2019

Jezabel Curbelo ,
Lucia Duarte ,
Thierry Alboussière Open the ORCID record for Thierry Alboussière [Opens in a new window] ,
Fabien Dubuffet ,
Stéphane Labrosse Open the ORCID record for Stéphane Labrosse [Opens in a new window]  and
Yanick Ricard Open the ORCID record for Yanick Ricard [Opens in a new window]
Jezabel Curbelo
Affiliation:
Departamento de Matemáticas, Facultad de Ciencias, Universidad Autónoma de Madrid, 28049 Madrid, Spain Instituto de Ciencias Matemáticas, CSIC–UAM–UC3M–UCM, 28049 Madrid, Spain
Lucia Duarte
Affiliation:
Department of Physics and Astronomy, University of Exeter, North Park Road, Exeter EX4 4QL, UK
Thierry Alboussière*
Affiliation:
Université de Lyon, UCBL, ENSL, CNRS, LGL-TPE, 69622 Villeurbanne, France
Fabien Dubuffet
Affiliation:
Université de Lyon, UCBL, ENSL, CNRS, LGL-TPE, 69622 Villeurbanne, France
Stéphane Labrosse
Affiliation:
Université de Lyon, UCBL, ENSL, CNRS, LGL-TPE, 69622 Villeurbanne, France
Yanick Ricard
Affiliation:
Université de Lyon, UCBL, ENSL, CNRS, LGL-TPE, 69622 Villeurbanne, France
*
†Email address for correspondence: thierry.alboussiere@ens-lyon.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We developed a numerical method for the set of equations governing fully compressible convection in the limit of infinite Prandtl numbers. Reduced models have also been analysed, such as the anelastic approximation and the anelastic liquid approximation. The tests of our numerical schemes against self-consistent criteria have shown that our numerical simulations are consistent from the point of view of energy dissipation, heat transfer and entropy budget. The equation of state of an ideal gas has been considered in this work. Specific effects arising because of the compressibility of the fluid are studied, like the scaling of viscous dissipation and the scaling of the heat flux contribution due to the mechanical power exerted by viscous forces. We analysed the solutions obtained with each model (fully compressible model, anelastic and anelastic liquid approximations) in a wide range of dimensionless parameters and determined the errors induced by each approximation with respect to the fully compressible solutions. Based on a rationale on the development of the thermal boundary layers, we can explain reasonably well the differences between the fully compressible and anelastic models, in terms of both the heat transfer and viscous dissipation dependence on compressibility. This could be mostly an effect of density variations on thermal diffusivity. Based on the different forms of entropy balance between exact and anelastic models, we find that a necessary condition for convergence of the anelastic results to the exact solutions is that the product 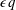$\unicode[STIX]{x1D716}q$ must be small compared to unity, where $\unicode[STIX]{x1D716}$ is the ratio of the superadiabatic temperature difference to the adiabatic difference, and 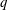$q$ is the ratio of the superadiabatic heat flux to the heat flux conducted along the adiabat. The same condition seems also to be associated with a convergence of the computed heat fluxes. Concerning the anelastic liquid approximation, we confirm previous estimates by Anufriev et al. (Phys. Earth Planet. Inter., vol. 152, 2005, pp. 163–190) and find that its results become generally close to those of the fully compressible model when 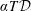$\unicode[STIX]{x1D6FC}T{\mathcal{D}}$ is small compared to unity, where $\unicode[STIX]{x1D6FC}$ is the isobaric thermal expansion coefficient, 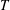$T$ is the temperature (here 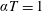$\unicode[STIX]{x1D6FC}T=1$ for an ideal gas) and 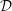${\mathcal{D}}$ is the dissipation number.

JFM classification

Compressible Flows: Compressible Flows Convection: Convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 873 , 25 August 2019 , pp. 646 - 687
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alboussière, T. & Ricard, Y. 2013 Reflections on dissipation associated with thermal convection. J. Fluid Mech. 725, 1469–7645.Google Scholar
Alboussière, T. & Ricard, Y. 2017 Rayleigh–Bénard stability and the validity of quasi-Boussinesq or quasi-anelastic liquid approximations. J. Fluid Mech. 817, 264–305.Google Scholar
Anufriev, A. P., Jones, C. A. & Soward, A. M. 2005 The Boussinesq and anelastic liquid approximations for convection in the Earth’s core. Phys. Earth Planet. Inter. 152, 163–190.10.1016/j.pepi.2005.06.004Google Scholar
Bercovici, D., Schubert, G. & Glatzmaier, G. A. 1992 Three-dimensional convection of an infinite-Prandtl-number compressible fluid in a basally heated spherical shell. J. Fluid Mech. 239, 683–719.Google Scholar
Boussinesq, J. 1903 Théorie Analytique de la Chaleur, vol. 2, pp. 157–161. Gauthier-Villars.Google Scholar
Braginsky, S. I. & Roberts, P. H. 1995 Equations governing convection in Earth’s core and the geodynamo. Geophys. Astrophys. Fluid Dyn. 79, 1–97.Google Scholar
Davis, T. A. 2004 Algorithm 832: UMFPACK v4.3 – an unsymmetric-pattern multifrontal method. Trans. Math. Softw. 30 (2), 196–199.10.1145/992200.992206Google Scholar
Davis, T. A. 2006 Direct Methods for Sparse Linear Systems. SIAM.Google Scholar
Doering, C. R. & Constantin, P. 1996 Variational bounds on energy dissipation in incompressible flows. III. Convection. Phys. Rev. E 53 (6), 5957–5981.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.Google Scholar
Hewitt, J. M., McKenzie, D. P. & Weiss, N. O. 1975 Dissipative heating in convective flows. J. Fluid Mech. 68 (4), 721–738.Google Scholar
Hurlburt, N. E., Toomre, J. & Massaguer, J. M. 1984 Two-dimensional compressible convection extending over multiple scale heights. Astrophys. J. 282, 557–573.Google Scholar
Jimenez, J. & Zufiria, J. A. 1987 A boundary-layer analysis of Rayleigh–Bénard convection at large Rayleigh number. J. Fluid Mech. 178, 53–71.Google Scholar
Lantz, S. R. & Fan, Y. 1999 Anelastic magnetohydrodynamic equations for modeling solar and stellar convection zones. Astrophys. J. 121, 247–264.Google Scholar
Malkus, W. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225, 196–212.Google Scholar
Malkus, W. V. R.1964 Boussinesq equations and convection energetics. Rep. Woods Hole Oceanographic Institute.Google Scholar
McKenzie, D. & Jarvis, G. 1980 The conversion of heat into mechanical work by mantle convection. J. Geophys. Res. 85 (B11), 6093–6096.Google Scholar
Oberbeck, A. 1879 Über die Wärmeleitung des Flüssigkeiten bei Berücksichtigung des Strömungen infolge von Temperaturdifferenzen. Ann. Phys. Chem. 7, 271–292.Google Scholar
Ogura, Y. & Phillips, N. A. 1961 Scale analysis of deep and shallow convection in the atmosphere. J. Atmos. Sci. 19, 173–179.Google Scholar
Ricard, Y. 2015 Physics of Mantle Convection, Treatise on Geophysics, vol. 7. Cambridge University Press.Google Scholar
Spiegel, E. A. & Veronis, G. 1971 On the Boussinesq approximation for a compressible fluid. Astrophys. J. 131, 442–447.Google Scholar
Tilgner, A. 2011 Convection in an ideal gas at high Rayleigh numbers. Phys. Rev. E 84 (2), 026323.Google Scholar
Verhoeven, J., Wiesehöfer, T. & Stellmach, S. 2015 Anelastic versus fully compressible turbulent Rayleigh–Bénard convection. Astrophys. J. 805 (1), 62–76.10.1088/0004-637X/805/1/62Google Scholar
Verhoogen, J. 1980 Energetics of the Earth, pp. 67–89. National Academy Press.Google Scholar
Wu, X. Z. & Libchaber, A. 1991 Non-Boussinesq effects in free thermal convection. Phys. Rev. A 43, 2833–2839.Google Scholar