Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-06-20T22:16:13.018Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the secondary load cycle for a monopile in irregular deep water waves

Published online by Cambridge University Press:  26 June 2018

Bjørn Hervold Riise Open the ORCID record for Bjørn Hervold Riise [Opens in a new window] ,
John Grue Open the ORCID record for John Grue [Opens in a new window] ,
Atle Jensen  and
Thomas B. Johannessen
Bjørn Hervold Riise*
Affiliation:
Department of Mathematics, University of Oslo, PO Box 1053 Blindern, NO-0316 Oslo, Norway DNV GL Oil & Gas, PO Box 300, NO-1322 Høvik, Norway
John Grue
Affiliation:
Department of Mathematics, University of Oslo, PO Box 1053 Blindern, NO-0316 Oslo, Norway
Atle Jensen
Affiliation:
Department of Mathematics, University of Oslo, PO Box 1053 Blindern, NO-0316 Oslo, Norway
Thomas B. Johannessen
Affiliation:
DNV GL Oil & Gas, PO Box 300, NO-1322 Høvik, Norway
*
†Email address for correspondence: bjorn.riise@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Laboratory experiments with a bottom hinged surface-piercing cylinder, exposed to irregular deep water waves, are used to investigate high-frequency forcing. The focus is on the secondary load cycle, a strongly nonlinear phenomenon regarding the wave load on a vertical cylinder, first identified by Grue et al. (1993 Preprint Series. Mechanics and Applied Mathematics, pp. 1–30. University of Oslo, available at http://urn.nb.no/URN:NBN:no-52740; 1994 Ninth International Workshop on Water Waves and Floating Bodies (ed. M. Ohkusu), pp. 77–81, available at http://iwwwfb.org). For a total of 2166 single wave events, the force above 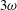$3\unicode[STIX]{x1D714}$ (where 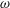$\unicode[STIX]{x1D714}$ is the governing wave frequency) is used to identify and split the strongly nonlinear forces into two peaks: a high-frequency peak closely correlated in time with the wave crest when the total load is positive and a high-frequency peak defining the secondary load cycle which occurs close in time to the wave zero downcrossing when the total load is negative. The two peaks are studied by regression analysis as a function of either the Keulegan–Carpenter number (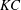$KC$) or the Froude number (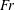$Fr$). Regarding the secondary load cycle, the best correlation is found with 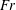$Fr$. The speed of the travelling edge of the undisturbed wave approximates the fluid velocity. A threshold value separating between small and large forces is found for 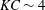$KC\sim 4$–5, indicating effects of flow separation. Alternatively, the threshold occurs for 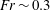$Fr\sim 0.3$–0.4, indicating local wave effects at the scale of the cylinder diameter. The findings suggest that both effects are present and important.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Wave breaking
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 849 , 25 August 2018 , R1
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chaplin, J. R., Rainey, R. C. T. & Yemm, R. W. 1997 Ringing of a vertical cylinder in waves. J. Fluid Mech. 350, 119–147.Google Scholar
Chau, F. P. & Eatock Taylor, R. 1992 Second-order wave diffraction by a vertical cylinder. J. Fluid Mech. 240, 571–599.Google Scholar
Chella, M. A., Tørum, A. & Myrhaug, D. 2012 An overview of wave impact forces on offshore wind turbine substructures. Energy Procedia 20, 217–226.Google Scholar
Faltinsen, O. M., Newman, J. N. & Vinje, T. 1995 Nonlinear wave loads on a slender vertical cylinder. J. Fluid Mech. 289, 179–198.Google Scholar
Goda, Y. & Suzuki, Y. 1976 Estimation of incident and reflected waves in random wave experiments. In Coastal Engineering 1976, pp. 828–845. American Society of Civil Engineers.Google Scholar
Grue, J. 2002 On four highly nonlinear phenomena in wave theory and marine hydrodynamics. Appl. Ocean Res. 24 (5), 261–274.Google Scholar
Grue, J., Bjørshol, G. & Strand, Ø. 1993 Higher harmonic wave exciting forces on a vertical cylinder. In Preprint Series. Mechanics and Applied Mathematics, pp. 1–30. University of Oslo. Available at http://urn.nb.no/URN:NBN:no-52740.Google Scholar
Grue, J., Bjørshol, G. & Strand, Ø. 1994 Nonlinear wave loads which may generate ‘ringing’ responses of offshore structures. In Ninth International Workshop on Water Waves and Floating Bodies (ed. Ohkusu, M.), pp. 77–81. Available at http://iwwwfb.org.Google Scholar
Grue, J. & Huseby, M. 2002 Higher-harmonic wave forces and ringing of vertical cylinders. Appl. Ocean Res. 24 (4), 203–214.Google Scholar
Hasselmann, K., Barnett, T. P., Bouws, E., Carlson, H., Cartwright, D. E., Enke, K., Ewing, J. A., Gienapp, H., Hasselmann, D. E., Kruseman, P., Meerburg, A., Müller, P., Olbers, D. J., Richter, K., Sell, W. & Walden, H. 1973 Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Tech. Rep. Deutches Hydrographisches Institut.Google Scholar
Kristiansen, T. & Faltinsen, O. M. 2017 Higher harmonic wave loads on a vertical cylinder in finite water depth. J. Fluid Mech. 833, 773–805.Google Scholar
MacCamy, R. C. & Fuchs, R. A.1954 Wave forces on piles: a diffraction theory. Tech. Rep. Tech. Mem. No. 69. Beach Erosion Board.Google Scholar
Malenica, Š. & Molin, B. 1995 Third-harmonic wave diffraction by a vertical cylinder. J. Fluid Mech. 302, 203–229.Google Scholar
Newman, J. N. 1996a Nonlinear scattering of long waves by a vertical cylinder. In Waves and Nonlinear Processes in Hydrodynamics (ed. Grue, J., Gjevik, B. & Weber, J. E.), pp. 91–102. Springer.Google Scholar
Newman, J. N. 1996b The second-order wave force on a vertical cylinder. J. Fluid Mech. 320, 417–443.Google Scholar
Paulsen, B. T., Bredmose, H., Bingham, H. B. & Jacobsen, N. G. 2014 Forcing of a bottom-mounted circular cylinder by steep regular water waves at finite depth. J. Fluid Mech. 755, 1–34.Google Scholar
Rainey, R. C. T. 2007 Weak or strong nonlinearity: the vital issue. J. Engng Maths 58 (1–4), 229–249.Google Scholar
Riise, B. H., Grue, J., Jensen, A. & Johannessen, T. B.2018 High frequency resonant response of a monopile in irregular deep water waves. J. Fluid Mech. (submitted).Google Scholar
Sarpkaya, T. 1986 Force on a circular cylinder in viscous oscillatory flow at low Keulegan–Carpenter numbers. J. Fluid Mech. 165, 61–71.Google Scholar
Sheikh, R. & Swan, C. 2005 The interaction between steep waves and a vertical, surface-piercing column. J. Offshore Mech. Arctic Engng 127, 31–38.Google Scholar
Stansberg, C. T. 1997 Comparing ringing loads from experiments with cylinders of different diameters; an empirical study. In The Eighth Conference on the Behaviour of Offshore Structures (BOSS ’97), pp. 95–109. Pergamon.Google Scholar
Swan, C. & Sheikh, R. 2015 The interaction between steep waves and a surface-piercing column. Phil. Trans. R. Soc. Lond. A 373, 20140114.Google Scholar
Taylor, R. E. & Hung, S. M. 1987 Second order diffraction forces on a vertical cylinder in regular waves. Appl. Ocean Res. 9 (1), 19–30.Google Scholar
Tromans, P., Swan, C. & Masterton, S.2006 Nonlinear potential flow forcing: the ringing of concrete gravity based structures. Tech. Rep. HSE Report 468. Health and Safety Executive, UK.Google Scholar
Zhen, G., Bingham, H. B., Nicholls-Lee, R. et al. 2015 Offshore renewable energy. In 19th International Ship and Offshore Structures Congress, Taylor & Francis.Google Scholar