Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-20T01:14:46.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-steady columnar motions in rotating stratified Boussinesq fluids: exact Lagrangian and Eulerian description

Published online by Cambridge University Press:  05 December 2011

Evsei I. Yakubovich  and
Victor I. Shrira
Evsei I. Yakubovich
Affiliation:
Institute for Applied Physics, Russian Academy of Sciences, N.-Novgorod, 603600, Russia
Victor I. Shrira*
Affiliation:
Department of Mathematics, EPSAM, Keele University, Keele ST5 5BG, UK
*
†Email address for correspondence: v.i.shrira@keele.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper aims to narrow the gap between the Lagrangian and Eulerian descriptions of rotating stratified fluids. To this end, without loss of generality the primitive Lagrangian equations with arbitrary oriented time-dependent rotation 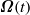and arbitrary stable stratification have been simplified and made more amenable for analysis. The bulk of the work is concerned with developing in parallel exact Lagrangian and Eulerian descriptions of a particular interesting class of motions of rotating stratified incompressible Boussinesq fluids: the vertically uniform columnar motions. The Lagrangian description is confined to ideal fluids, while the Eulerian one includes viscosity and diffusivity. Assuming the rotation axis to be parallel to gravity, with the rotation rate being an arbitrary function of time, and the buoyancy frequency to be constant, it is found that for vertically uniform motions there is always an exact split into horizontal and vertical subsystems. Evolution of the horizontal velocities and displacements is governed by the classical equations of two-dimensional incompressible hydrodynamics, only slightly modified by accounting for the variable rotation rate. These equations are independent of stratification and vertical motions. The Coriolis term is potential and can be incorporated into pressure. The vertical motions represent a manifestation of packets of inertia–gravity waves with strictly horizontal wavevectors, and are exactly described by linear equations independently of the wave amplitudes. They do not depend on rotation, either constant or variable. The wavepackets do not interact with each other or with horizontal motions. For ideal fluids or those with Rayleigh friction there are explicit solutions describing these motions for arbitrary initial conditions. The Cauchy problem for the columnar motions in ideal fluids is found to be well posed. Thus there is a natural extension of well-studied two-dimensional incompressible hydrodynamics which retains the property of the absence of vortex stretching: all two-dimensional flows could be ‘dressed up’ by adding appropriate vertical motions of a rotating stratified fluid. All the columnar motions could be described in such a way. The examined columnar motions exist under arbitrary relations between the parameters of rotation and stratification and, in particular, without rotation. In the limit of strong rotation one recovers the results known in the literature, in particular, under additional assumptions of small amplitude and steadiness of motions the solutions describe the classical Taylor–Proudman columns.

JFM classification

Mathematical Foundations: General fluid mechanics Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 691 , 25 January 2012 , pp. 417 - 439
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abrashkin, A. A. & Yakubovich, E. I. 1984 Planar rotational flows of an ideal fluid. Sov. Phys. Dokl. 29 (5), 370–371.Google Scholar
2. Abrashkin, A. A. & Yakubovich, E. I. 2006 Vortex dynamics in the Lagrangian description (in Russian). FIZMATLIT ISBN 5-9221-0725-9.Google Scholar
3. Babin, A., Mahalov, A., Nicolaenko, B. & Zhou, Y. 1997 On the asymptotic regimes of the strongly stratified limit of rotating Boussinesq equations. Theor. Comput. Fluid Dyn. 9, 223–251.CrossRefGoogle Scholar
4. Bennett, A. 2006 Lagrangian Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
5. Billant, P. & Chomaz, J.-M. 2000 Theoretical analysis of the zigzag instability of a vertical columnar vortex pair in a strongly stratified fluid. J. Fluid Mech. 419, 29–63.CrossRefGoogle Scholar
6. Davidson, P. A., Staplehurst, P. J. & Dalziel, S. B. 2006 On the evolution of eddies in a rapidly rotating system. J. Fluid Mech. 557, 135–144.CrossRefGoogle Scholar
7. Dritschel, D. 2010 IUTAM symposium on turbulence in the atmosphere and oceans. Proceedings of the IUTAM Symposium on Turbulence in the Atmosphere and Oceans, Cambridge, UK, December 8–12, 2008. Springer.CrossRefGoogle Scholar
8. Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
9. Huntley, H. S., Lipphard, B. L. & Kirwan, A. D. 2011 Lagrangian predictability assessed in the East China Sea. Ocean Model. 36 (1–2), 163–178.CrossRefGoogle Scholar
10. Kato, T. 1967 On the classical solutions of the two-dimensional non-stationary Euler equation. Arch. Rat. Mech. Anal. 25, 188–200.CrossRefGoogle Scholar
11. Korn, G. A. & Korn, T. M. 2000 Mathematical Handbook for Scientists and Engineers. Dover.Google Scholar
12. Lamb, H. 1932 Hydrodynamics, 6th edn. Cambridge University Press.Google Scholar
13. Landau, L. D. & Lifshitz, 1976 Course of Theoretical Physics: Mechanics, 3rd edn. Butterworth-Heinemann.Google Scholar
14. LeBlond, P. H. & Mysak, L. A. 1978 Waves in the Ocean. Elsevier.Google Scholar
15. Milne-Thomson, L. 1974 Theoretical Hydrodynamics. Dover.Google Scholar
16. Miropol’sky, Y. Z. 2001 Dynamics of internal gravity waves in the ocean. Kluwer.CrossRefGoogle Scholar
17. Pedlosky, J. 1992 Geophysical Fluid Dynamics. Springer.Google Scholar
18. Pinchover, Y. & Rubinstein, J. 2005 An Introduction to Partial Differential Equations. Cambridge University Press.CrossRefGoogle Scholar
19. Proudman, J. 1916 On a motion of solids in liquids possessing vorticity. Proc. R. Soc. Lond. A92, 408–424.Google Scholar
20. Riley, J. J. & Lelong, M.-P. 2000 Fluid motions in the presence of strong stable stratification. Annu. Rev. Fluid Mech. 32, 613–657.CrossRefGoogle Scholar
21. Tabaei, A. & Akylas, T. R. 2003 Nonlinear internal gravity wave beams. J. Fluid Mech. 482, 141–161.CrossRefGoogle Scholar
22. Taylor, G. I. 1917 Motion of solids in fluids when the flow is not irrotational. Proc. R. Soc. Lond. A 93, 99–113.Google Scholar
23. de la Torre Juares, M. 2009 Taylor–Proudman columns in non-hydrostatic divergent baroclinic and barotropic flows. Q. J. R. Meteorol. Soc. 135, 2179–2184.CrossRefGoogle Scholar
24. Yakubovich, E. I. & Zenkovich, D. A. 2001 Matrix approach to Lagrangian fluid dynamics. J. Fluid Mech. 443, 167–196.CrossRefGoogle Scholar
25. Zeitlin, V. & Kambe, T. 1993 Two-dimensional ideal magnetohydrodynamics and differential geometry. J. Phys. A 26, 5025–5031.CrossRefGoogle Scholar