Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-25T13:56:30.328Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-resonant viscous theory for the stability of a fluid-filled gyroscope

Published online by Cambridge University Press:  16 October 2009

JEAN-PIERRE LAMBELIN ,
FRANÇOIS NADAL ,
ROMAIN LAGRANGE  and
ARTHUR SARTHOU
JEAN-PIERRE LAMBELIN
Affiliation:
Commissariat à l'Energie Atomique, CESTA, 33114 Le Barp, France
FRANÇOIS NADAL*
Affiliation:
Commissariat à l'Energie Atomique, CESTA, 33114 Le Barp, France
ROMAIN LAGRANGE
Affiliation:
IRPHE, CNRS, Universit Aix Marseille I & II, 49 rue Joliot-Curie, 13013 Marseille, France
ARTHUR SARTHOU
Affiliation:
Université Bordeaux I, TREFLE-ENSCPB, UMR CNRS 8508, 16 avenue Pey-Berland, 33607 Pessac Cedex, France
*
†Email address for correspondence: Francois.Nadal@cea.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In the case of a gyroscope including a cylindrical fluid-filled cavity, the classic Poinsot's coning motion can become unstable. For certain values of the solid inertia ratio, the coning angle opens under the effect of the hydrodynamic torque. The coupled dynamics of such a non-solid system is ruled by four dimensionless numbers: the small viscous parameter ε = Re−1/2 (where Re denotes the Reynolds number), the fluid–solid inertia ratio κ which quantifies the proportion of liquid relative to the total mass of the gyroscope, the solid inertia ratio σ and the aspect ratio h of the cylindrical cavity. The calculation of the hydrodynamic torque on the solid part of the gyroscope requires the preliminary evaluation of the possibly resonant flow inside the cavity. The hydrodynamic scaling used to derive such a flow essentially depends on the relative values of κ and ε. For small values of the ratio 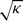/ε (compared to 1), Gans derived an expression of the growth rate of the coning angle. The principles of Gans' approach (Gans, AIAA J., vol. 22, 1984, pp. 1465–1471) are briefly recalled but the details of the whole calculation are not given. At the opposite limit, that is for large values of 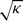/ε, the dominating flow is given by a linear inviscid theory. In order to take account of viscous effects, we propose a direct method involving an exhaustive calculation of the flow at order ε. We show that the deviations from Stewartson's inviscid theory (Stewartson, J. Fluid Mech., vol. 5, 1958, p. 577) do not originate from the viscous shear at the walls but rather from the bulk pressure at order ε related to the Ekman suction. Physical contents of Wedemeyer's heuristic theory (Wedemeyer, BRL Report N 1325, 1966) are analysed in the view of our analytical results. The latter are tested numerically in a large range of parameters. Complete Navier–Stokes (NS) equations are solved in the cavity. The hydrodynamic torque obtained by numerical integration of the stress is used as a forcing term in the coupled fluid–solid equations. Numerical results and analytical predictions show a fairly good quantitative agreement.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 639 , 25 November 2009 , pp. 167 - 194
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

D'Amico, W. P. 1977 Inertial mode corrections for the large amplitude motion of a liquid-filled gyroscope. PhD Thesis, University of Delaware, Newark.Google Scholar
D'Amico, W. P. & Rogers, T. H. 1981 Yaw instabilities produced by rapidly rotating, highly viscous liquids. AIAA paper 81-0224.Google Scholar
Fortin, M. & Glowinski, R. 1982 Méthodes de Lagrangien augmenté. Application à la résolution numérique de problèmes aux limites. Paris, Dunod.Google Scholar
Fultz, D. 1959 A note on overstability and elastoid-inertia oscillations of Kelvin, Solberg and Bjerknes. J. Meteorol. 16, 199–208.2.0.CO;2>CrossRefGoogle Scholar
Gans, R. F. 1970 On the precession of a resonant cylinder. J. Fluid Mech. 476, 865–872.CrossRefGoogle Scholar
Gans, R. F. 1984 Dynamics of a near-resonant fluid-filled gyroscope. AIAA J. 22, 1465–1471.CrossRefGoogle Scholar
Garg, S. C., Furunoto, N. & Vanyo, J. P. 1986 Spacecraft nutational instability prediction by energy dissipation measurements. J. Guid. 9 (3), 357–361.CrossRefGoogle Scholar
Greenhill, A. G. 1880 On the general motion of a liquid ellipsoid. Proc. Camb. Phil. Soc. 4 (4).Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Harlow, F. H & Welsh, J. E. 1965 Numerical calculation of time dependant viscous incompressible flows. Phys. Fluids 8, 2182–2189.CrossRefGoogle Scholar
Karpov, B. G. 1962 Experimental observations of the dynamic behaviour of liquid-filled shell. Tech. Rep. BRL Report 1171. Aberdeen Proving Ground, MD.Google Scholar
Karpov, B. G. 1965 The effect of Reynolds number on resonance. Tech. Rep. BRL Report 1302. Aberdeen Proving Ground, MD.Google Scholar
Kerswell, R. R. 1999 Secondary instabilities in rapidly rotating fluids: inertial wave breakdown. J. Fluid Mech. 382, 283–306.CrossRefGoogle Scholar
Kerswell, R. R. & Barenghi, C. F. 1995 On the viscous decay rates of inertial waves in a rotating circular cylinder J. Fluid Mech. 285, 203–214.CrossRefGoogle Scholar
Kobine, J. J. 1995 Inertial wave dynamics in a rotating and precessing cylinder. J. Fluid Mech. 303, 233–352.CrossRefGoogle Scholar
Kobine, J. J. 1996 Azimuthal flow associated with inertial wave resonance in a precessing cylinder. J. Fluid Mech. 319, 387–406.CrossRefGoogle Scholar
Kudlick, M. 1966 On the transient motions in a contained rotating fluid. PhD thesis, Massachussets Institute of Technology, Cambridge, MA.Google Scholar
Lagrange, R., Meunier, P., Eloy, C. & Nadal, F. 2008 Instability of a fluid inside a precessing cylinder. Phys. Fluids 20, 081701.Google Scholar
Mahalov, A. 1993 The instability of rotating fluid columns subjected to a weak external Coriolis force. Phys. Fluids A 5 (4), 891–900.CrossRefGoogle Scholar
Manasseh, R. 1992 Breakdown regimes of inertia waves in precessing cylinder. J. Fluid Mech. 243, 261–296.CrossRefGoogle Scholar
Manasseh, R. 1994 Distortions of inertia waves in a rotating fluid cylinder forced near its fundamental mode resonance. J. Fluid Mech. 265, 345–370.Google Scholar
Manasseh, R. 1996 Nonlinear behaviour of contained inertia waves. J. Fluid Mech. 315, 151–173.Google Scholar
McEwan, A. D. 1970 Inertial oscillations in a rotating fluid cylinder. J. Fluid Mech. 40, 603–640.CrossRefGoogle Scholar
Meunier, P., Eloy, C., Lagrange, R. & Nadal, F. 2008 Rotating fluid cylinder subject to weak precession. J. Fluid Mech. 599, 405–440.Google Scholar
Milne, E. A. 1940 On the stability of a liquid-filled shell (U). EBD report No. 6.Google Scholar
Murphy, C. H. 1982 Angular motion of a spinning projectile with a viscous payload. Tech. Rep. ARBRL-TR-02422. US Army Ballistic Research Laboratory, Aberdeen Proving Ground, MD.Google Scholar
Scott, W. E. & D'Amico, W. P. 1973 Amplitude-dependent behavior of a liquid-filled gyroscope. J. Fluid Mech. 60, 751–758.CrossRefGoogle Scholar
Stewartson, K. 1958 On the stability of a spinning top containing liquid. J. Fluid Mech. 5, 577–592.Google Scholar
Thomson, W. Sir 1880 Vibrations of a columnar vortex. Phil. Mag. 10, 155–168.CrossRefGoogle Scholar
Thomson, R. 1970 Diurnal tides and shear instabilities in a rotating cylinder. J. Fluid Mech. 40, 737–751.CrossRefGoogle Scholar
Vanyo, J. P. 1993 Rotating Fluids in Engineering and Science. Dover.Google Scholar
Vincent, S. & Caltagirone, J.-P. 2000 A one-cell local multigrid method for solving unsteady incompressible multiphase flow. J. Comput. Phys. 163, 172–215.CrossRefGoogle Scholar
van der Vorst, H. A. 1992 Bi-CGSTAB: a fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear system. SIAM J. Sci. Stat. Comput. 13, 631–644.CrossRefGoogle Scholar
Waleffe, F. 1989 The three-dimensional instability of a strained vortex and its relation to turbulence. PhD thesis, Massachussets Institute of Technology, Cambridge, MA.Google Scholar
Ward, G. N. 1959 Appendix to K. Stewartson “On the stability of a spinning top containing liquid”. J. Fluid Mech. 5, 577–592.Google Scholar
Watson, G. N. 1952 Theory of Bessel Functions. Cambridge University Press.Google Scholar
Wedemeyer, E. H. 1965 Dynamics of a liquid-filled shell: theory of viscous corrections to Stewartson's stability problem. BRL Report N 1287. US Army Ballistic Research Laboratory, Aberdeen Proving Ground, MD.Google Scholar
Wedemeyer, E. H. 1966 Viscous corrections to Stewartson's stability criterion. BRL Report N 1325. US Army Ballistic Research Laboratory, Aberdeen Proving Ground, MD.Google Scholar
Whiting, R. D. & Gerber, N. 1981 Dynamics of a liquid-filled gyroscope: update of theory and experiment. Tech. Rep. ARBRL-TR-02221. US Army Ballistic Research Laboratory, Aberdeen Proving Ground, MD.Google Scholar