Article contents
A nonlinear small-deformation theory for transient droplet electrohydrodynamics
Published online by Cambridge University Press: 28 November 2016
Abstract
The deformation of a viscous liquid droplet suspended in another liquid and subject to an applied electric field is a classic multiphase flow problem best described by the Melcher–Taylor leaky dielectric model. The main assumption of the model is that any net charge in the system is concentrated on the interface between the two liquids as a result of the jump in Ohmic currents from the bulk. Upon application of the field, the drop can either attain a steady prolate or oblate shape with toroidal circulating flows both inside and outside arising from tangential stresses on the interface due to action of the field on the surface charge distribution. Since the pioneering work of Taylor (Proc. R. Soc. Lond. A, vol. 291, 1966, pp. 159–166), there have been numerous computational and theoretical studies to predict the deformations measured in experiments. Most existing theoretical models, however, have either neglected transient charge relaxation or nonlinear charge convection by the interfacial flow. In this work, we develop a novel small-deformation theory accurate to second order in electric capillary number 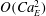 $O(Ca_{E}^{2})$ for the complete Melcher–Taylor model that includes transient charge relaxation, charge convection by the flow, as well as transient shape deformation. The main result of the paper is the derivation of coupled evolution equations for the induced electric multipoles and for the shape functions describing the deformations on the basis of spherical harmonics. Our results, which are consistent with previous models in the appropriate limits, show excellent agreement with fully nonlinear numerical simulations based on an axisymmetric boundary element formulation and with existing experimental data in the small-deformation regime.
$O(Ca_{E}^{2})$ for the complete Melcher–Taylor model that includes transient charge relaxation, charge convection by the flow, as well as transient shape deformation. The main result of the paper is the derivation of coupled evolution equations for the induced electric multipoles and for the shape functions describing the deformations on the basis of spherical harmonics. Our results, which are consistent with previous models in the appropriate limits, show excellent agreement with fully nonlinear numerical simulations based on an axisymmetric boundary element formulation and with existing experimental data in the small-deformation regime.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
Footnotes
Present address: Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK.
References
- 70
- Cited by



