Hostname: page-component-5c6d5d7d68-wtssw Total loading time: 0 Render date: 2024-08-16T07:13:23.700Z Has data issue: false hasContentIssue false
  • English
  • Français

The near-field pressure radiated by planar high-speed free-shear-flow turbulence

Published online by Cambridge University Press:  26 October 2017

David A. Buchta Open the ORCID record for David A. Buchta [Opens in a new window]  and
Jonathan B. Freund Open the ORCID record for Jonathan B. Freund [Opens in a new window]
David A. Buchta
Affiliation:
Department of Mechanical Science and Engineering, University of Illinois at Urbana–Champaign, Urbana, IL 61801, USA
Jonathan B. Freund*
Affiliation:
Department of Mechanical Science and Engineering, University of Illinois at Urbana–Champaign, Urbana, IL 61801, USA Department of Aerospace Engineering, University of Illinois at Urbana–Champaign, Urbana, IL 61801, USA
*
†Email address for correspondence: jbfreund@illinois.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

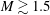Jets with Mach numbers $M\gtrsim 1.5$ are well known to emit an intense, fricative, so-called crackle sound, having steep compressions interspersed with weaker expansions that together yield a positive pressure skewness 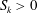$S_{k}>0$. Its shock-like features are obvious hallmarks of nonlinearity, although a full explanation of the skewness is lacking, and wave steepening alone is understood to be insufficient to describe its genesis. Direct numerical simulations of high-speed free-shear flows for Mach numbers 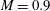$M=0.9$, 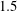$1.5$, 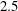$2.5$ and 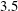$3.5$ in the Reynolds number range 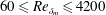$60\leqslant Re_{\unicode[STIX]{x1D6FF}_{m}}\leqslant 4200$ are used to examine the mechanisms leading to such pressure signals, especially the pressure skewness. For 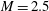$M=2.5$ and 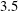$3.5$, the pressure immediately adjacent the turbulence already has the large 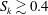$S_{k}\gtrsim 0.4$ associated with jet crackle. It also has a surprisingly complex three-dimensional structure, with locally high pressures at compression-wave intersections. This structure is transient, and it simplifies as radiating waves subsequently merge through nonlinear mechanisms to form the relatively distinct and approximately two-dimensional Mach-like waves deduced from laboratory visualizations. A transport equation for 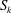$S_{k}$ is analysed to quantify factors affecting its development. The viscous dissipation that decreases 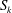$S_{k}$ is balanced by a particular nonlinear flux, which is (of course) absent in linear acoustic propagation and confirmed to be independent of the simulated Reynolds numbers. Together these effects maintain an approximately constant 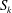$S_{k}$ in the near acoustic field.

JFM classification

Acoustics: Aeroacoustics Acoustics: Jet noise Turbulent Flows: Shear layer turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 832 , 10 December 2017 , pp. 383 - 408
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, A. T. & Freund, J. B. 2012 Source mechanisms of jet crackle. In 18th AIAA/CEAS Aeroacoustics Conference. AIAA.Google Scholar
Baars, W. J. & Tinney, C. E. 2014 Shock-structures in the acoustic field of a Mach 3 jet with crackle. J. Sound Vib. 333 (12), 2539–2553.Google Scholar
Baars, W. J., Tinney, C. E., Wochner, M. S. & Hamilton, M. F. 2014 On cumulative nonlinear acoustic waveform distortions from high-speed jets. J. Fluid Mech. 749, 331–366.Google Scholar
Bogey, C. & Bailly, C. 2004 A family of low dispersive and low dissipative explicit schemes for flow and noise computations. J. Comput. Phys. 194 (1), 194–214.Google Scholar
Buchta, D. A.2016 Crackle noise from high-speed free-shear-flow turbulence. PhD thesis, University of Illinois at Urbana–Champaign.Google Scholar
Buchta, D. A., Anderson, A. T. & Freund, J. B. 2014 Near-field shocks radiated by high-speed free-shear-flow turbulence. In 20th AIAA/CEAS Aeroacoustics Conference. AIAA.Google Scholar
Chobotov, V. & Powell, A.1957 On the prediction of acoustic environments from rockets. Tech. Rep. E.M.-7-7. Ramo-Wooldridge Corporation.Google Scholar
Crighton, D. G. 1986 Nonlinear acoustic propagation of broadband noise. In Recent Advances in Aeroacoustics (ed. Krothapalli, A. & Smith, C. A.), pp. 411–454. Springer.Google Scholar
Darke, R. & Freund, J. B. 2001 Mach wave radiation from a jet at Mach 1.92. Phys. Fluids 13 (9), S3.Google Scholar
De Cacqueray, N. & Bogey, C. 2014 Noise of an overexpanded Mach 3.3 jet: non-linear propagation effects and correlations with flow. Intl J. Aeroacoust. 13 (7), 607–632.Google Scholar
Debisschop, J. R., Chambres, O. & Bonnet, J. P. 1994 Velocity field characteristics in supersonic mixing layers. Exp. Therm. Fluid Sci. 9 (2), 147–155.Google Scholar
Elliott, G. S. & Samimy, M. 1990 Compressibility effects in free shear layers. Phys. Fluids A 2 (7), 1231–1240.Google Scholar
Ffowcs Williams, J. E. 1963 The noise from turbulence convected at high speed. Phil. Trans. R. Soc. Lond. 255, 469–503.Google Scholar
Ffowcs Williams, J. E., Simson, J. & Virchis, V. J. 1975 ‘Crackle’: an annoying component of jet noise. J. Fluid Mech. 71, 251–271.Google Scholar
Fiévet, R., Tinney, C. E., Baars, W. J. & Hamilton, M. F. 2015 Coalescence in the sound field of a laboratory-scale supersonic jet. AIAA J. 54 (1), 254–265.Google Scholar
Freund, J. B. 1997 Proposed inflow/outflow boundary condition for direct computation of aerodynamic sound. AIAA J. 35 (4), 740–742.Google Scholar
Freund, J. B., Lele, S. K. & Moin, P. 2000 Numerical simulation of a Mach 1.92 turbulent jet and its sound field. AIAA J. 38 (11), 2023–2031.Google Scholar
Gee, K. L., Neilsen, T. B. & Atchley, A. A. 2013a Skewness and shock formation in laboratory-scale supersonic jet data. J. Acoust. Soc. Am. 133 (6), 491–497.Google Scholar
Gee, K. L., Neilsen, T. B., Downing, J. M., James, M. M., McKinley, R. L., McKinley, R. C. & Wall, A. T. 2013b Near-field shock formation in noise propagation from a high-power jet aircraft. J. Acoust. Soc. Am. 133 (2), 88–93.CrossRefGoogle ScholarPubMed
Gee, K. L., Neilsen, T. B., Wall, A. T., Downing, J. M., James, M. M. & McKinley, R. L. 2016 Propagation of crackle-containing jet noise from high-performance engines. Noise Control Engng J. 64 (1), 1–12.CrossRefGoogle Scholar
Gee, K. L., Shepherd, M. R., Falco, L. E., Atchley, A. A., Ukeiley, L. S., Jansen, B. J. & Seiner, J. M. 2007a Identification of nonlinear and near-field effects in jet noise using nonlinearity indicators. In 13th AIAA/CEAS Aeroacoustics Conference. AIAA.Google Scholar
Gee, K. L., Sparrow, V. W., Atchley, A. & Gabrielson, T. B. 2007b On the perception of crackle in high-amplitude jet noise. AIAA J. 45 (3), 593–598.Google Scholar
Gee, K. L., Sparrow, V. W., James, M. M., Downing, J. M., Hobbs, C. M., Gabrielson, T. B. & Atchley, A. A. 2008 The role of nonlinear effects in the propagation of noise from high-power jet aircraft. J. Acoust. Soc. Am. 123 (6), 4082–4093.Google Scholar
Goebel, S. G. & Dutton, J. C. 1991 Experimental study of compressible turbulent mixing layers. AIAA J. 29 (4), 538–546.Google Scholar
Kleinman, R. & Freund, J. B. 2008 The sound from mixing layers simulated with different ranges of turbulence scales. Phys. Fluids 20 (10), 101503.Google Scholar
Krothapalli, A., Arakeri, V. & Greska, B. 2003a Mach wave radiation: a review and an extension. In 41st Aerospace Sciences Meeting and Exhibit. AIAA.Google Scholar
Krothapalli, A., Greska, B. & Arakeri, V. 2005 High-speed jet noise reduction using microjets. In Combustion Processes in Propulsion, pp. 231–244.Google Scholar
Krothapalli, A., Venkatakrishnan, L. & Lourenco, L. 2000 Crackle: a dominant component of supersonic jet mixing noise. In 6th AIAA/CEAS Aeroacoustics Conference. AIAA.Google Scholar
Krothapalli, A., Venkatakrishnan, L., Lourenco, L., Greska, B. & Elavarasan, R. 2003b Turbulence and noise suppression of a high-speed jet by water injection. J. Fluid Mech. 491, 131–159.Google Scholar
Kuo, C.-W., Veltin, J. & McLaughlin, D. K. 2012 Effects of jet noise source distribution on acoustic far-field measurements. Intl J. Aeroacoust. 11 (7–8), 885–915.Google Scholar
Laufer, J., Schlinker, R. & Kaplan, R. E. 1976 Experiments on supersonic jet noise. AIAA J. 14 (4), 489–497.Google Scholar
Lighthill, M. J. 1956 Viscosity effects in sound waves of finite amplitude. In Surveys in Mechanics (ed. Batchelor, G. K. & Davies, R. M.), pp. 250–351. Cambridge University Press.Google Scholar
Lighthill, M. J. 1993 Some aspects of the aeroacoustics of extreme-speed jets. In Symposium on Aerodynamics & Aeroacoustics (ed. Fung, K. Y.), pp. 39–48. World Scientific.Google Scholar
Martens, S., Spyropoulos, J. T. & Nagel, Z. 2011 The effect of chevrons on crackle-engine and scale model results. Proc. ASME Turbomach. Expo. 1, 315–326.Google Scholar
Mcinerny, S. A. 1996 Launch vehicle acoustics. Part II: statistics of the time domain data. J. Aircraft 33 (3), 518–523.CrossRefGoogle Scholar
Mora, P., Heeb, N., Kastner, J., Gutmark, E. J. & Kailasanath, K. 2014 Impact of heat on the pressure skewness and kurtosis in supersonic jets. AIAA J. 52 (4), 777–787.Google Scholar
Mora, P., Kastner, J., Gutmark, E. J. & Kailasanath, K. 2015 Investigation of a heated supersonic jet chevrons nozzle. In 53rd AIAA Aerospace Sciences Meeting. AIAA.Google Scholar
Mora, P., Kastner, J., Heeb, N., Munday, D., Gutmark, E. J., Liu, J. & Kailasanath, K. 2012 The impact of heat on the near and far-field pressure skewness in supersonic jets. In 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. AIAA.Google Scholar
Murray, N. E. & Lyons, G. W. 2016 On the convection velocity of source events related to supersonic jet crackle. J. Fluid Mech. 793, 477–503.Google Scholar
Neilsen, T. B., Gee, K. L., Wall, A. T., James, M. M. & Atchley, A. A. 2013 Comparison of supersonic full-scale and laboratory-scale jet data and the similarity spectra for turbulent mixing noise. In Proceedings of Meetings on Acoustics.Google Scholar
Nichols, J. W., Lele, S. K., Ham, F. E., Martens, S. & Spyropoulos, J. T. 2013a Crackle noise in heated supersonic jets. Trans. ASME J. Engng Gas Turbines Power 135 (5), 051202.Google Scholar
Nichols, J. W., Lele, S. K. & Spyropoulos, J. T. 2013b The source of crackle noise in heated supersonic jets. In 19th AIAA/CEAS Aeroacoustics Conference. AIAA.Google Scholar
Oertel, H. 1979 Kinematics of Mach waves inside and outside supersonic jets. In Recent Developments in Theoretical and Experimental Fluid Mechanics (ed. Müller, U., Roesner, K.G. & Schmidt, B.), pp. 121–136. Springer.Google Scholar
Pantano, C. & Sarkar, S. 2002 A study of compressibility effects in the high-speed turbulent shear layer using direct simulation. J. Fluid Mech. 451, 329–371.Google Scholar
Papamoschou, D. & Debiasi, M. 2001 Directional suppression of noise from a high-speed jet. AIAA J. 39 (3), 380–387.Google Scholar
Petitjean, B. P. & McLaughlin, D. K. 2003 Experiments on the nonlinear propagation of noise from supersonic jets. In 9th AIAA/CEAS Aeroacoustics Conference. AIAA.Google Scholar
Petitjean, B. P., Viswanathan, K. & McLaughlin, D. K. 2006 Acoustic pressure waveforms measured in high speed jet noise experiencing nonlinear propagation. Intl J. Aeroacoust. 5 (2), 193–215.CrossRefGoogle Scholar
Schlinker, R. H., Liljenberg, S. A., Polak, D. R., Post, K. A., Chipman, C. T. & Stern, A. M. 2007 Supersonic jet noise source characteristics and propagation: engine and model scale. In 13th AIAA/CEAS Aeroacoustics Conference. AIAA.Google Scholar
Schlinker, R. H., Simonich, J. C., Reba, R. A., Colonius, T. & Ladeinde, F. 2008 Decomposition of high speed jet noise: source characteristics and propagation effects. In AIAA/CEAS Aeroacoustics Conference. AIAA.Google Scholar
Szewczyk, V. M.1978 The role of flow acoustic interaction in jet noise studies. PhD thesis, University of Southampton.Google Scholar
Tanna, H. K., Dean, P. D. & Burrin, R. H.1976 Turbulent mixing noise data. Tech. Rep. AFAPL-TR-76-65. The generation and radiation of supersonic jet noise, U.S. Air Force Aero Propulsion Laboratory Technical Report Laboratory.Google Scholar
Taylor, G. I. 1910 The conditions necessary for discontinuous motion in gases. Proc. R. Soc. Lond. A 84 (571), 371–377.Google Scholar
Thompson, K. W. 1987 Time dependent boundary conditions for hyperbolic systems. J. Comput. Phys. 68 (1), 1–24.Google Scholar
Thompson, P. A. 1988 Compressible-Fluid Dynamics. McGraw-Hill.Google Scholar
Whitham, G. B. 1974 Linear and Nonlinear Waves. Wiley.Google Scholar