Article contents
Mutual inductance instability of the tip vortices behind a wind turbine
Published online by Cambridge University Press: 26 August 2014
Abstract
Two modal decomposition techniques are employed to analyse the stability of wind turbine wakes. A numerical study on a single wind turbine wake is carried out focusing on the instability onset of the trailing tip vortices shed from the turbine blades. The numerical model is based on large-eddy simulations (LES) of the Navier–Stokes equations using the actuator line (ACL) method to simulate the wake behind the Tjæreborg wind turbine. The wake is perturbed by low-amplitude excitation sources located in the neighbourhood of the tip spirals. The amplification of the waves travelling along the spiral triggers instabilities, leading to breakdown of the wake. Based on the grid configurations and the type of excitations, two basic flow cases, symmetric and asymmetric, are identified. In the symmetric setup, we impose a 120° symmetry condition in the dynamics of the flow and in the asymmetric setup we calculate the full 360° wake. Different cases are subsequently analysed using dynamic mode decomposition (DMD) and proper orthogonal decomposition (POD). The results reveal that the main instability mechanism is dispersive and that the modal growth in the symmetric setup arises only for some specific frequencies and spatial structures, e.g. two dominant groups of modes with positive growth (spatial structures) are identified, while breaking the symmetry reveals that almost all the modes have positive growth rate. In both setups, the most unstable modes have a non-dimensional spatial growth rate close to 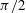 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\pi /2$ and they are characterized by an out-of-phase displacement of successive helix turns leading to local vortex pairing. The present results indicate that the asymmetric case is crucial to study, as the stability characteristics of the flow change significantly compared to the symmetric configurations. Based on the constant non-dimensional growth rate of disturbances, we derive a new analytical relationship between the length of the wake up to the turbulent breakdown and the operating conditions of a wind turbine.
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\pi /2$ and they are characterized by an out-of-phase displacement of successive helix turns leading to local vortex pairing. The present results indicate that the asymmetric case is crucial to study, as the stability characteristics of the flow change significantly compared to the symmetric configurations. Based on the constant non-dimensional growth rate of disturbances, we derive a new analytical relationship between the length of the wake up to the turbulent breakdown and the operating conditions of a wind turbine.
JFM classification
- Type
- Papers
- Information
- Creative Commons
- The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
- Copyright
- © 2014 Cambridge University Press
References
- 134
- Cited by


