Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-25T11:02:07.779Z Has data issue: false hasContentIssue false
  • English
  • Français

A multilayer shallow model for dry granular flows with the ${\it\mu}(I)$-rheology: application to granular collapse on erodible beds

Published online by Cambridge University Press:  07 June 2016

E. D. Fernández-Nieto ,
J. Garres-Díaz Open the ORCID record for J. Garres-Díaz [Opens in a new window] ,
A. Mangeney  and
G. Narbona-Reina
E. D. Fernández-Nieto
Affiliation:
Dpto. Matemática Aplicada I. ETS Arquitectura – Universidad de Sevilla, Avda. Reina Mercedes S/N, 41012-Sevilla, Spain
J. Garres-Díaz*
Affiliation:
IMUS & Dpto. Matemática Aplicada I. ETS Arquitectura – Universidad de Sevilla, Avda. Reina Mercedes S/N, 41012-Sevilla, Spain
A. Mangeney
Affiliation:
Seismology team, Institut de Physique du Globe de Paris, Université Paris Diderot, Sorbonne Paris Cité, 75238, Paris, France ANGE team, CEREMA, INRIA, Lab. J. Louis Lions, 75252, Paris, France
G. Narbona-Reina
Affiliation:
Dpto. Matemática Aplicada I. ETS Arquitectura – Universidad de Sevilla, Avda. Reina Mercedes S/N, 41012-Sevilla, Spain
*
†Email address for correspondence: jgarres@us.es
Get access Rights & Permissions [Opens in a new window]

Abstract

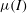In this work we present a multilayer shallow model to approximate the Navier–Stokes equations with the ${\it\mu}(I)$-rheology through an asymptotic analysis. The main advantages of this approximation are (i) the low cost associated with the numerical treatment of the free surface of the modelled flows, (ii) the exact conservation of mass and (iii) the ability to compute two-dimensional profiles of the velocities in the directions along and normal to the slope. The derivation of the model follows Fernández-Nieto et al. (J. Comput. Phys., vol. 60, 2014, pp. 408–437) and introduces a dimensional analysis based on the shallow flow hypothesis. The proposed first-order multilayer model fully satisfies a dissipative energy equation. A comparison with steady uniform Bagnold flow – with and without the sidewall friction effect – and laboratory experiments with a non-constant normal profile of the downslope velocity demonstrates the accuracy of the numerical model. Finally, by comparing the numerical results with experimental data on granular collapses, we show that the proposed multilayer model with the 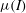${\it\mu}(I)$-rheology qualitatively reproduces the effect of the erodible bed on granular flow dynamics and deposits, such as the increase of runout distance with increasing thickness of the erodible bed. We show that the use of a constant friction coefficient in the multilayer model leads to the opposite behaviour. This multilayer model captures the strong change in shape of the velocity profile (from S-shaped to Bagnold-like) observed during the different phases of the highly transient flow, including the presence of static and flowing zones within the granular column.

JFM classification

Mathematical Foundations: Computational methods Non-Newtonian Flows: Rheology Geophysical and Geological Flows: Shallow water flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 798 , 10 July 2016 , pp. 643 - 681
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Audusse, E. 2005 A multilayer Saint-Venant model: derivation and numerical validation. Discrete Continuous Dyn. Syst. B 5 (2), 189–214.Google Scholar
Audusse, E., Bouchut, F., Bristeau, M., Klein, R. & Perthame, B. 2004 A fast and stable well-balanced scheme with hydrostatic reconstruction for shallow water flows. SIAM J. Sci. Comput. 25 (6), 2050–2065.CrossRefGoogle Scholar
Audusse, E., Bristeau, M., Perthame, B. & Sainte-Marie, J. 2011a A multilayer Saint-Venant system with mass exchanges for shallow water flows. Derivation and numerical validation. ESAIM: Math. Modelling Numer. Anal. 45, 169–200.CrossRefGoogle Scholar
Audusse, E., Bristeau, M.-O. & Decoene, A. 2008 Numerical simulations of 3D free surface flows by a multilayer Saint-Venant model. Intl J. Numer. Meth. Fluids 56 (3), 331–350.Google Scholar
Audusse, E., Bristeau, M-O., Pelanti, M. & Sainte-Marie, J. 2011b Approximation of the hydrostatic Navier–Stokes system for density stratified flows by a multilayer model: kinetic interpretation and numerical solution. J. Comput. Phys. 230 (9), 3453–3478.CrossRefGoogle Scholar
Baker, J. L., Barker, T. & Gray, J. M. N. T. 2016 A two-dimensional depth-averaged 𝜇(I)-rheology for dense granular avalanches. J. Fluid Mech. 787, 367–395.Google Scholar
Barker, T., Schaeffer, D. G., Bohorquez, P. & Gray, J. M. N. T. 2015 Well-posed and ill-posed behaviour of the 𝜇(I)-rheology for granular flow. J. Fluid Mech. 779, 794–818.Google Scholar
Bercovier, M. & Engelman, M. 1980 A finite-element method for incompressible non-Newtonian flows. J. Comput. Phys. 36 (3), 313–326.Google Scholar
Berger, C., McArdell, B. W. & Schlunegger, F. 2011 Direct measurement of channel erosion by debris flows, Illgraben, Switzerland. J. Geophys. Res. Earth Surf. 116 (F1), f01002.Google Scholar
Bermúdez, A. & Moreno, C. 1981 Duality methods for solving variational inequalities. Comput. Math. Appl. 7 (1), 43–58.Google Scholar
Bouchut, F. 2004 Nonlinear Stability of Finite Volume Methods for Hyperbolic Conservation Laws: and Well-Balanced Schemes for Sources. Springer.CrossRefGoogle Scholar
Bouchut, F., Fernández-Nieto, E. D., Mangeney, A. & Narbona-Reina, G. 2015 A two-phase shallow debris flow model with energy balance. ESAIM: M2AN 49 (1), 101–140.Google Scholar
Bouchut, F., Ionescu, I. & Mangeney, A. 2016 An analytic approach for the evolution of the static-flowing interface in viscoplastic granular flows. Commun. Math. Sci. (to appear).Google Scholar
Capart, H., Hung, C.-Y. & Stark, C. P. 2015 Depth-integrated equations for entraining granular flows in narrow channels. J. Fluid Mech. 765, R4.Google Scholar
Chauchat, J. & Médale, M. 2010 A three-dimensional numerical model for incompressible two-phase flow of a granular bed submitted to a laminar shearing flow. Comput. Meth. Appl. Mech. Engng 199 (912), 439–449.Google Scholar
Chauchat, J. & Médale, M. 2014 A three-dimensional numerical model for dense granular flows based on the 𝜇(I)-rheology. J. Comput. Phys. 256 (0), 696–712.Google Scholar
Conway, S. J., Decaulne, A., Balme, M. R., Murray, J. B. & Towner, M. C. 2010 A new approach to estimating hazard posed by debris flows in the westfjords of Iceland. Geomorphology 114 (4), 556–572.Google Scholar
Delannay, R., Valance, A., Mangeney, A., Roche, O. & Richard, P. 2015 Granular and particle-laden flows: from laboratory experiments to field observations. J. Phys. D (submitted).Google Scholar
Edwards, A. N. & Gray, J. M. N. T. 2015 Erosion-deposition waves in shallow granular free-surface flows. J. Fluid Mech. 762, 35–67.Google Scholar
Faccanoni, G. & Mangeney, A. 2013 Exact solution for granular flows. Intl J. Numer. Anal. Meth. Geomech. 37 (10), 1408–1433.Google Scholar
Farin, M., Mangeney, A. & Roche, O. 2014 Fundamental changes of granular flow dynamics, deposition, and erosion processes at high slope angles: insights from laboratory experiments. J. Geophys. Res. Earth Surf. 119 (3), 504–532.Google Scholar
Fernández-Nieto, E. D., Bouchut, F., Bresch, D., Castro Díaz, M. J. & Mangeney, A. 2008 A new Savage–Hutter type model for submarine avalanches and generated tsunami. J. Comput. Phys. 227 (16), 7720–7754.Google Scholar
Fernández-Nieto, E. D., Koné, E. H. & Chacón Rebollo, T. 2014 A multilayer method for the hydrostatic Navier–Stokes equations: a particular weak solution. J. Sci. Comput. 60 (2), 408–437.Google Scholar
GDR MiDi 2004 On dense granular flows. Eur. Phys. J. E 14 (4), 341–365.Google Scholar
Glowinski, R. & Tallec, P. L. 1989 Augmented Lagrangian and Operator-splitting Methods in Nonlinear Mechanics. SIAM.Google Scholar
Gray, J. M. N. T. & Edwards, A. N. 2014 A depth-averaged 𝜇(I)-rheology for shallow granular free-surface flows. J. Fluid Mech. 755, 503–534.Google Scholar
Gray, J. M. N. T., Tai, Y.-C. & Noelle, S. 2003 Shock waves, dead zones and particle-free regions in rapid granular free-surface flows. J. Fluid Mech. 491, 161–181.CrossRefGoogle Scholar
Ionescu, I. R., Mangeney, A., Bouchut, F. & Roche, R. 2015 Viscoplastic modeling of granular column collapse with pressure-dependent rheology. J. Non-Newtonian Fluid Mech. 219 (0), 1–18.CrossRefGoogle Scholar
Iverson, R. M., Reid, M. E., Logan, M., LaHusen, R. G., Godt, J. W. & Griswold, J. P. 2011 Positive feedback and momentum growth during debris-flow entrainment of wet bed sediment. Nature Geosci. 4 (2), 116–121.CrossRefGoogle Scholar
Jessop, D. E., Kelfoun, K., Labazuy, P., Mangeney, A., Roche, O., Tillier, J.-L., Trouillet, M. & Thibault, G. 2012 LiDAR derived morphology of the 1993 Lascar pyroclastic flow deposits, and implication for flow dynamics and rheology. J. Volcanol. Geotherm. Res. 245–246 (0), 81–97.Google Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2005 Crucial role of sidewalls in granular surface flows: consequences for the rheology. J. Fluid Mech. 541, 167–192.Google Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2006 A constitutive law for dense granular flows. Nature 441 (7094), 727–730.Google Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2007 Initiation of granular surface flows in a narrow channel. Phys. Fluids 19 (8), 088102.Google Scholar
Lagrée, P.-Y., Staron, L. & Popinet, S. 2011 The granular column collapse as a continuum: validity of a two-dimensional Navier–Stokes with a 𝜇(I)-rheology. J. Fluid Mech. 686, 378–408.CrossRefGoogle Scholar
Lusso, C., Bouchut, F., Ern, A. & Mangeney, A.2015a A simplified model for static/flowing dynamics in thin-layer flows of granular materials with yield. Proc. R. Soc. Lond. A (submitted).Google Scholar
Lusso, C., Ern, A., Bouchut, F., Mangeney, A., Farin, M. & Roche, O.2015b Two-dimensional simulation by regularization of free surface viscoplastic flows with Drucker–Prager yield stress and application to granular collapse. J. Comput. Phys. (submitted).Google Scholar
Mangeney, A., Bouchut, F., Thomas, N., Vilotte, J. P. & Bristeau, M. O. 2007 Numerical modeling of self-channeling granular flows and of their levee-channel deposits. J. Geophys. Res. Earth Surf. 112 (F2), f02017.Google Scholar
Mangeney, A., Roche, O., Hungr, O., Mangold, N., Faccanoni, G. & Lucas, A. 2010 Erosion and mobility in granular collapse over sloping beds. J. Geophys. Res. Earth Surf. 115 (F3).Google Scholar
Mangeney-Castelnau, A., Bouchut, F., Vilotte, J. P., Lajeunesse, E., Aubertin, A. & Pirulli, M. 2005 On the use of Saint-Venant equations to simulate the spreading of a granular mass. J. Geophys. Res. Solid Earth 110, B09103.Google Scholar
Mangeney-Castelnau, A., Vilotte, J.-P., Bristeau, M. O., Perthame, B., Bouchut, F., Simeoni, C. & Yerneni, S. 2003 Numerical modeling of avalanches based on Saint Venant equations using a kinetic scheme. J. Geophys. Res. Solid Earth 108 (B11), 2527.Google Scholar
Parés, C. 2006 Numerical methods for nonconservative hyperbolic systems: a theoretical framework. SIAM J. Numer. Anal. 44 (1), 300–321.CrossRefGoogle Scholar
Pirulli, M. & Mangeney, A. 2008 Results of back-analysis of the propagation of rock avalanches as a function of the assumed rheology. Rock Mech. Rock Engng 41 (1), 59–84.CrossRefGoogle Scholar
Pouliquen, O. 1999a On the shape of granular fronts down rough inclined planes. Phys. Fluids 11 (7).Google Scholar
Pouliquen, O. 1999b Scaling laws in granular flows down rough inclined planes. Phys. Fluids 11 (3), 542–548.Google Scholar
Pouliquen, O. & Forterre, Y. 2002 Friction law for dense granular flows: application to the motion of a mass down a rough inclined plane. J. Fluid Mech. 453, 133–151.Google Scholar
Sainte-Marie, J. 2011 Vertically averaged models for the free surface non-hydrostatic Euler system: derivation and kinetic interpretation. Math. Models Meth. Appl. Sci. 21 (03), 459–490.Google Scholar
Savage, S. B. & Hutter, K. 1989 The motion of a finite mass of granular material down a rough incline. J. Fluid Mech. 199, 177–215.Google Scholar
Schaeffer, D. 1987 Instability in the evolution equations describing incompressible granular flow. J. Differ. Equ. 66 (1), 19–50.Google Scholar
Silbert, L. E., Ertaş, D., Grest, G. S., Halsey, T. C., Levine, D. & Plimpton, S. J. 2001 Granular flow down an inclined plane: Bagnold scaling and rheology. Phys. Rev. E 64, 051302.Google Scholar
Staron, L., Lagrée, P.-Y. & Popinet, S. 2012 The granular silo as a continuum plastic flow: the hour-glass versus the clepsydra. Phys. Fluids 24 (10).CrossRefGoogle Scholar
Staron, L., Lagrée, P.-Y. & Popinet, S. 2014 Continuum simulation of the discharge of the granular silo: a validation test for the 𝜇(I)-visco-plastic flow law. Eur. Phys. J. E 37 (1).Google Scholar