Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-28T05:41:52.194Z Has data issue: false hasContentIssue false
  • English
  • Français

The motion of an axisymmetric body falling in a tube at moderate Reynolds numbers

Published online by Cambridge University Press:  02 January 2013

Nicolas Brosse  and
Patricia Ern
Nicolas Brosse
Affiliation:
Université de Toulouse; INPT, UPS; Institut de Mécanique des Fluides de Toulouse; Allée Camille Soula, F-31400 Toulouse, France CNRS; Institut de Mécanique des Fluides de Toulouse; F-31400 Toulouse, France
Patricia Ern*
Affiliation:
Université de Toulouse; INPT, UPS; Institut de Mécanique des Fluides de Toulouse; Allée Camille Soula, F-31400 Toulouse, France CNRS; Institut de Mécanique des Fluides de Toulouse; F-31400 Toulouse, France
*
†Email address for correspondence: ern@imft.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

This study concerns the rectilinear and periodic paths of an axisymmetric solid body (short-length cylinder and disk of diameter 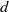$d$ and thickness $h$) falling in a vertical tube of diameter 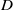$D$. We investigated experimentally the influence of the confinement ratio (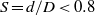$S= d/ D\lt 0. 8$) on the motion of the body, for different aspect ratios (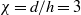$\chi = d/ h= 3$, 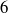$6$ and 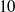$10$), Reynolds numbers (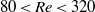$80\lt Re\lt 320$) and a density ratio between the fluid and the body close to unity. For a given body, the Reynolds number based on its mean vertical velocity is observed to decrease when 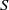$S$ increases. The critical Reynolds number for the onset of the periodic motion decreases with 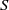$S$ in the case of thin bodies (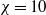$\chi = 10$), whereas it appears unaffected by 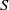$S$ for thicker bodies (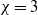$\chi = 3$ and 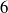$6$). The characteristics of the periodic motion are also strongly modified by the confinement ratio. A thick body (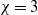$\chi = 3$) tends to go back to a rectilinear path when $S$ increases, while a thin body (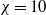$\chi = 10$) displays oscillations of growing amplitude with 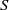$S$ until it touches the tube (at about 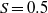$S= 0. 5$). For a given aspect ratio, however, the amplitudes of the oscillations follow a unique curve for all 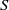$S$, which depends only on the relative distance of the Reynolds number to the threshold of path instability. In parallel, numerical simulations of the wake of a body held fixed in a uniform confined flow were carried out. The simulations allowed us to determine in this configuration the effect of the confinement ratio on the thresholds for wake instability (loss of axial symmetry at 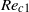$R{e}_{c 1} $ and loss of stationarity at 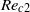$R{e}_{c 2} $) and on the maximal velocity 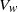${V}_{w} $ in the recirculating region of the stationary axisymmetric wake. The evolution with 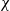$\chi $ and 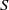$S$ of 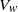${V}_{w} $ at 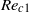$R{e}_{c 1} $ was used to define a Reynolds number 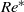$R{e}^{\ast} $. Remarkably, for a freely moving body, 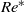$R{e}^{\ast} $ remains almost constant when 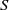$S$ varies, regardless of the nature of the path.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Vortex Flows: Vortex shedding Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 714 , 10 January 2013 , pp. 238 - 257
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auguste, F. 2010 Instabilités de sillage générées derrière un corps solide cylindrique, fixe ou mobile dans un fluide visqueux. PhD thesis, Université Paul Sabatier, Toulouse, France:http://thesesups.ups-tlse.fr/1186/.Google Scholar
Auguste, F., Fabre, D. & Magnaudet, J. 2010 Bifurcations in the wake of a thick circular disk. Theor. Comput. Fluid Dyn. 24, 305–313.Google Scholar
Bhattacharyya, S. & Maiti, D. 2006 Vortex shedding suppression for laminar flow past a square cylinder near a plane wall: a two-dimensional analysis. Acta Mechanica 184, 15–31.Google Scholar
Camarri, S. & Giannetti, F. 2007 On the inversion of the von Kármán street in the wake of a confined square cylinder. J. Fluid Mech. 574, 169–178.CrossRefGoogle Scholar
Camarri, S. & Giannetti, F. 2010 Effect of confinement on three-dimensional stability in the wake of a circular cylinder. J. Fluid Mech. 642, 477–487.Google Scholar
Chen, J. H., Pritchard, W. G. & Tavener, S. J. 1995 Bifurcation for flow past a cylinder between parallel planes. J. Fluid Mech. 284, 23–41.Google Scholar
Chhabra, R. P., Agarwal, S. & Chaudhary, K. 2003 A note on wall effect on the terminal falling velocity of a sphere in quiescent Newtonian media in cylindrical tubes. Powder Technol. 129 (1–3), 53–58.Google Scholar
Cliffe, K. A., Spence, A. & Tavener, S. J. 2000 O(2)-symmetry breaking bifurcation: with application to the flow past a sphere in a pipe. Intl J. Numer. Meth. Fluids 32 (2), 175–200.Google Scholar
Clift, R., Grace, J. & Weber, M. E. 1978 Bubbles, Drops and Particles. Academic Press.Google Scholar
Deloze, T. 2011 Couplage fluide–solide appliqué à l’étude de mouvement d’une sphère libre dans un tube vertical. PhD thesis, Université Louis Pasteur, Strasbourg, France.Google Scholar
Ern, P., Fernandes, P. C., Risso, F. & Magnaudet, J. 2007 Evolution of wake structure and wake-induced loads along the path of freely rising axisymmetric bodies. Phys. Fluids 19 (11), 113302.Google Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of freely rising or falling bodies. Annu. Rev. Fluid Mech. 44, 97–121.CrossRefGoogle Scholar
Feng, J., Hu, H. H. & Joseph, D. D. 1994 Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid. Part 1. Sedimentation. J. Fluid Mech. 261, 95–134.Google Scholar
Fernandes, P. C., Ern, P., Risso, F. & Magnaudet, J. 2005 On the zigzag dynamics of freely moving axisymmetric bodies. Phys. Fluids 17 (9), 098107.CrossRefGoogle Scholar
Fernandes, P. C., Risso, F., Ern, P. & Magnaudet, J. 2007 Oscillatory motion and wake instability of freely rising axisymmetric bodies. J. Fluid Mech. 573, 479–502.Google Scholar
Figueroa-Espinoza, B., Zenit, R. & Legendre, D. 2008 The effect of confinement on the motion of a single clean bubble. J. Fluid Mech. 616, 476–480.Google Scholar
Kim, I., Elghobashi, S. & Sirignano, W. A. 1993 Three-dimensional flow over two spheres placed side by side. J. Fluid Mech. 246, 465–488.Google Scholar
Legendre, D. & Magnaudet, J. 1998 The lift force on a spherical bubble in a viscous linear shear flow. J. Fluid Mech. 368, 81–126.Google Scholar
Legendre, D., Magnaudet, J. & Mougin, G. 2003 Hydrodynamic interactions between two spherical bubbles rising side by side in a viscous liquid. J. Fluid Mech. 497, 133–166.Google Scholar
Maheshwari, A., Chhabra, R. P. & Biswas, G. 2006 Effect of blockage on drag and heat transfer from a single sphere and an in-line array of three spheres. Powder Technol. 168 (2), 74–83.Google Scholar
Sahin, M. & Owens, R. G. 2004 A numerical investigation of wall effects up to high blockage ratios on two-dimensional flow past a confined circular cylinder. Phys. Fluids 16 (5), 1305–1320.Google Scholar
Takemura, F. & Magnaudet, J. 2003 The transverse force on clean and contaminated bubbles rising near a vertical wall at moderate Reynolds number. J. Fluid Mech. 495, 235–253.Google Scholar
Tavener, S. J. 1994 Stability of the O(2)-symmetric flow past a sphere in a pipe. Phys. Fluids 6 (12), 3884–3892.Google Scholar
Wham, R. M., Basaran, O. A. & Byers, C. H. 1996 Wall effects on flow past solid spheres at finite Reynolds number. Ind. Engng Chem. Res. 35 (3), 864–874.Google Scholar
Yu, Z., Phan-Thien, N. & Tanner, R. I. 2004 Dynamic simulation of sphere motion in a vertical tube. J. Fluid Mech. 518, 61–93.Google Scholar
Zovatto, L. & Pedrizzetti, G. 2001 Flow about a circular cylinder between parallel walls. J. Fluid Mech. 440, 1–25.Google Scholar