Hostname: page-component-848d4c4894-xfwgj Total loading time: 0 Render date: 2024-06-19T21:38:47.111Z Has data issue: false hasContentIssue false
  • English
  • Français

Morphological evolution of microscopic dewetting droplets with slip

Published online by Cambridge University Press:  04 September 2017

Tak Shing Chan Open the ORCID record for Tak Shing Chan [Opens in a new window] ,
Joshua D. McGraw ,
Thomas Salez ,
Ralf Seemann  and
Martin Brinkmann
Tak Shing Chan*
Affiliation:
Experimental Physics, Saarland University, D-66041 Saarbrücken, Germany
Joshua D. McGraw
Affiliation:
Département de Physique, Ecole Normale Supérieure/PSL Research University, CNRS, 24 rue Lhomond, 75005 Paris, France
Thomas Salez
Affiliation:
Laboratoire de Physico-Chimie Théorique, UMR CNRS Gulliver 7083, ESPCI Paris, PSL Research University, Paris, France Global Station for Soft Matter, Global Institution for Collaborative Research and Education, Hokkaido University, Sapporo, Japan
Ralf Seemann
Affiliation:
Experimental Physics, Saarland University, D-66041 Saarbrücken, Germany
Martin Brinkmann
Affiliation:
Experimental Physics, Saarland University, D-66041 Saarbrücken, Germany
*
†Email address for correspondence: tak.chan@physik.uni-saarland.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the dewetting of a droplet on a smooth horizontal solid surface for different slip lengths and equilibrium contact angles. Specifically, we solve for the axisymmetric Stokes flow using the boundary element method with (i) the Navier-slip boundary condition at the solid/liquid boundary and (ii) a time-independent equilibrium contact angle at the contact line. When decreasing the rescaled slip length 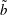$\tilde{b}$ with respect to the initial central height of the droplet, the typical non-sphericity of a droplet first increases, reaches a maximum at a characteristic rescaled slip length 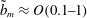$\tilde{b}_{m}\approx O(0.1{-}1)$ and then decreases. Regarding different equilibrium contact angles, two universal rescalings are proposed to describe the behaviour of the non-sphericity for rescaled slip lengths larger or smaller than 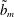$\tilde{b}_{m}$. Around 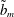$\tilde{b}_{m}$, the early time evolution of the profiles at the rim can be described by similarity solutions. The results are explained in terms of the structure of the flow field governed by different dissipation channels: elongational flows for 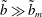$\tilde{b}\gg \tilde{b}_{m}$, friction at the substrate for $\tilde{b}\approx \tilde{b}_{m}$ and shear flows for 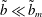$\tilde{b}\ll \tilde{b}_{m}$. Following the changes between these dominant dissipation mechanisms, our study indicates a crossover to the quasistatic regime when 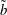$\tilde{b}$ is many orders of magnitude smaller than 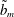$\tilde{b}_{m}$.

JFM classification

Interfacial Flows (free surface): Capillary flows Interfacial Flows (free surface): Contact lines Interfacial Flows (free surface): Interfacial Flows (free surface)
Type
Papers
Information
Journal of Fluid Mechanics , Volume 828 , 10 October 2017 , pp. 271 - 288
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bäumchen, O., Fetzer, R. & Jacobs, K. 2009 Reduced interfacial entanglement density affects the boundary conditions of polymer flow. Phys. Rev. Lett. 103, 247801.Google Scholar
Bocquet, L. & Charlaix, E. 2009 Nanofluidics, from bulk to interfaces. Chem. Soc. Rev. 39, 1073–1095.Google Scholar
Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolley, E. 2009 Wetting and spreading. Rev. Mod. Phys. 81, 739.Google Scholar
Chen, J.-D. 1988 Experiments on a spreading drop and its contact angle on a solid. J. Colloid Interface Sci. 122, 60–72.Google Scholar
Cox, R. G. 1986 The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech. 168, 169–194.Google Scholar
Cuenca, A. & Bodiguel, H. 2013 Submicron flow of polymer solutions: slippage reduction due to confinement. Phys. Rev. Lett. 110, 108304.CrossRefGoogle ScholarPubMed
Edwards, A. M. J., Ledesma-Aguilar, R., Newton, M. I., Brown, C. V. & McHale, G. 2016 Not spreading in reverse: the dewetting of a liquid film into a single drop. Sci. Adv. 2 (September), 1–11.Google Scholar
Falk, K., Sedlmeier, F., Joly, L., Netz, R. R. & Bocquet, L. 2010 Molecular origin of fast water transport in carbon nanotube membranes: superlubricity versus curvature dependent friction. Nano Lett. 10 (10), 4067–4073.Google Scholar
Fetzer, R., Jacobs, K., Münch, A., Wagner, B. & Witelski, T. P. 2005 New slip regimes and the shape of dewtting thin liquid films. Phys. Rev. Lett. 95, 127801.Google Scholar
Fetzer, R., Münch, A., Wagner, B., Rauscher, M. & Jacobs, K. 2007 Quantifying hydrodynamic slip: a comprehensive analysis of dewetting profiles. Langmuir 23, 10559–10566.Google Scholar
de Gennes, P. G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57, 827.Google Scholar
de Gennes, P.-G., Brochart-Wyart, F. & Quéré, D. 2003 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Springer.Google Scholar
Guido, S. & Villone, M. 1999 Measurement of interfacial tension by drop retraction analysis. J. Colloid Interface Sci. 209, 247–250.Google Scholar
Guo, S., Gao, M., Xiong, X.-M., Wang, Y.-J., Wang, X.-P., Sheng, P. & Tong, P. 2013 Direct measurement of friction of a fluctuating contact line. Phys. Rev. Lett. 111, 026101.Google Scholar
Haefner, S., Benzaquen, M., Bäumchen, O., Salez, T., Peters, R., McGraw, J. D., Jacobs, K., Raphaël, E. & Dalnoki-Veress, K. 2015 Influence of slip on the Plateau–Rayleigh instability on a fibre. Nat. Commun. 6 (May), 7409.Google Scholar
Huh, C. & Scriven, L. E. 1971 Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 35, 85–101.Google Scholar
Lauga, E., Brenner, M. P. & Stone, H. A. 2007 Microfluidics: the no-slip boundary condition. In Springer Handbook of Experimental Fluid Mechnaics (ed. Tropea, C., Foss, J. F. & Yarin, A.), pp. 1219–1240. Springer.Google Scholar
Lee, S. H. & Leal, L. G. 1982 The motion of a sphere in the presence of a deformable interface. II. A numerical study of the translation of a sphere normal to an interface. J. Colloid Interface Sci. 87 (1), 81–106.Google Scholar
Leger, L. 2003 Friction mechanisms and interfacial slip at fluid–solid interfaces. J. Phys.: Condens. Matter 15, S19.Google Scholar
van Lengerich, H. B. & Steen, P. H. 2012 Energy dissipation and the contact-line region of a spreading bridge. J. Fluid Mech. 703, 111–141.Google Scholar
McGraw, J. D., Chan, T. S., Maurer, S., Salez, T., Benzaquen, M., Raphaël, E., Brinkmann, M. & Jacobs, K. 2016 Slip-mediated dewetting of polymer microdroplets. Proc. Natl Acad. Sci. USA 113 (5), 1168–1173.Google Scholar
Neto, C., Evans, D. R., Bonaccurso, E., Butt, H.-J. & Craig, V. S. J. 2005 Boundary slip in newtonian liquids: a review of experimental studies. Rep. Prog. Phys. 68, 2859.CrossRefGoogle Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Flow. Cambridge University Press.Google Scholar
Redon, C., Brochard-Wyart, F. & Rondelez, F. 1991 Dynamics of dewetting. Phys. Rev. Lett. 66, 715–718.Google Scholar
Reiter, G. & Sharma, A. 2001 Auto-optimization of dewetting rates by rim instabilities in slipping polymer films. Phys. Rev. Lett. 87 (16), 166103.Google Scholar
Rivetti, M., Salez, T., Benzaquen, M., Raphaël, E. & Bäumchen, O. 2015 Universal contact-line dynamics at the nanoscale. Soft Matt. 11 (48), 9247–9253.Google Scholar
Sahimi, M. 1993 Flow phenomena in rocks: from continuum models to fractals, percolation, cellular automata, and simulated annealing. Rev. Mod. Phys. 65, 1393.Google Scholar
Setu, S. A., Dullens, R. P. a., Hernández-Machado, A., Pagonabarraga, I., Aarts, D. G. a. L. & Ledesma-Aguilar, R. 2015 Superconfinement tailors fluid flow at microscales. Nat. Commun. 6, 7297.CrossRefGoogle ScholarPubMed
Snoeijer, J. H. & Andreotti, B. 2013 Moving contact lines: scales, regimes, and dynamical transitions. Annu. Rev. Fluid Mech. 45, 269.Google Scholar
Snoeijer, J. H. & Eggers, J. 2010 Asymptotics of the dewetting rim. Phys. Rev. E 82, 056314.Google Scholar
Sui, Y., Ding, H. & Spelt, P. D. M. 2014 Numerical simulations of flows with moving contact lines. Annu. Rev. Fluid Mech. 46, 97–119.Google Scholar
Tanner, L. H. 1979 The spreading of silicone oil drops on horizontal surfaces. J. Phys. D: Appl. Phys. 12, 1473–1478.Google Scholar
Taylor, G. I. 1934 The formation of emulsions in definable fields of flow. Proc. R. Soc. Lond. A 146, 501.Google Scholar
Voinov, O. V. 1976 Hydrodynamics of wetting. Fluid Dyn. 11, 714–721; (English translation).Google Scholar
Weinstein, S. J. & Ruschak, K. J. 2004 Coating flows. Annu. Rev. Fluid Mech. 36, 29–53.Google Scholar
Winkels, K. G., Peters, I. R., Evangelista, F., Riepen, M., Daerr, A., Limat, L. & Snoeijer, J. H. 2011 Receding contact lines: from sliding drops to immersion lithography. Eur. Phys. J. Special Topics 192, 195.Google Scholar