Article contents
Modelling for robust feedback control of fluid flows
Published online by Cambridge University Press: 25 March 2015
Abstract
This paper addresses the problem of designing low-order and linear robust feedback controllers that provide a priori guarantees with respect to stability and performance when applied to a fluid flow. This is challenging, since whilst many flows are governed by a set of nonlinear, partial differential–algebraic equations (the Navier–Stokes equations), the majority of established control system design assumes models of much greater simplicity, in that they are: firstly, linear; secondly, described by ordinary differential equations (ODEs); and thirdly, finite-dimensional. With this in mind, we present a set of techniques that enables the disparity between such models and the underlying flow system to be quantified in a fashion that informs the subsequent design of feedback flow controllers, specifically those based on the 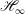 $\mathscr{H}_{\infty }$ loop-shaping approach. Highlights include the application of a model refinement technique as a means of obtaining low-order models with an associated bound that quantifies the closed-loop degradation incurred by using such finite-dimensional approximations of the underlying flow. In addition, we demonstrate how the influence of the nonlinearity of the flow can be attenuated by a linear feedback controller that employs high loop gain over a select frequency range, and offer an explanation for this in terms of Landahl’s theory of sheared turbulence. To illustrate the application of these techniques, an
$\mathscr{H}_{\infty }$ loop-shaping approach. Highlights include the application of a model refinement technique as a means of obtaining low-order models with an associated bound that quantifies the closed-loop degradation incurred by using such finite-dimensional approximations of the underlying flow. In addition, we demonstrate how the influence of the nonlinearity of the flow can be attenuated by a linear feedback controller that employs high loop gain over a select frequency range, and offer an explanation for this in terms of Landahl’s theory of sheared turbulence. To illustrate the application of these techniques, an 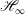 $\mathscr{H}_{\infty }$ loop-shaping controller is designed and applied to the problem of reducing perturbation wall shear stress in plane channel flow. Direct numerical simulation (DNS) results demonstrate robust attenuation of the perturbation shear stresses across a wide range of Reynolds numbers with a single linear controller.
$\mathscr{H}_{\infty }$ loop-shaping controller is designed and applied to the problem of reducing perturbation wall shear stress in plane channel flow. Direct numerical simulation (DNS) results demonstrate robust attenuation of the perturbation shear stresses across a wide range of Reynolds numbers with a single linear controller.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 24
- Cited by




