1 Introduction
Steady streaming, i.e. the generation of a mean flow in a fluid upon periodic actuation, has been studied for nearly two centuries (Faraday Reference Faraday1831; Rayleigh Reference Rayleigh1884). Typically, the generation of steady streaming requires one of the following three ingredients: (i) the presence of an oscillatory non-conservative body force, (ii) viscous attenuation of the oscillatory motion resulting in Reynolds stress or (iii) the presence of an oscillating deformable boundary (Riley Reference Riley2001; Chini, Malecha & Dreeben Reference Chini, Malecha and Dreeben2014). Acoustic streaming is a sub-class of steady streaming in which the oscillatory actuation arises from high-frequency sound waves and is generally associated with scenario (ii), with viscous torques being the primary agency for the development of the fluctuating vorticity field. In most cases, the streaming flow is weaker than the driving oscillatory flow and produces no appreciable feedback on the wave dynamics, thereby rendering itself amenable to theoretical analysis via a perturbation expansion approach (Nyborg Reference Nyborg, Hamilton and Blackstock1998; Vanneste & Bühler Reference Vanneste and Bühler2011; Nama, Huang & Costanzo Reference Nama, Huang and Costanzo2017). However, large-amplitude streaming flows, with speeds comparable to those of the driving oscillatory flow, can be realized for cases where viscosity is not the primary source of fluctuating vorticity (Amin Reference Amin1988; Riley & Trinh Reference Riley and Trinh2001; Červenka & Bednařík Reference Červenka and Bednařík2017). This latter class of streaming involves a strong coupling between the oscillatory acoustic fields and the concomitant streaming flow, posing significant numerical challenges owing to the widely separated temporal scales of these two physical phenomena. Michel & Chini (Reference Michel and Chini2019) investigate this important class of acoustic streaming by mathematically reformulating the temporal multiscale system as a dynamical system evolving strictly on a single (i.e. the streaming) time scale.
2 Overview
The article by Michel & Chini (Reference Michel and Chini2019) systematically extends a previous analysis by Chini et al. (Reference Chini, Malecha and Dreeben2014) to investigate strong coupling between the oscillatory flow and the baroclinically generated acoustic streaming. To this end, they consider a two-dimensional flow of an ideal gas in a long, thin channel with the upper and lower walls maintained at fixed but differing temperatures; see figure 1. This represents an excellent choice of system for study since a thin channel dynamically constrains the acoustic wave to maintain its first-mode wall-normal structure, simplifying the analysis of the acoustic wave. Furthermore, this configuration ensures that the leading-order (wall-parallel) fluctuating pressure gradient is orthogonal to the imposed background density gradient, thereby yielding a crucial baroclinic contribution to the generation of fluctuating vorticity.
A primary distinction between this work and earlier acoustic streaming studies is that the streaming flow arises at
 $O(\unicode[STIX]{x1D716})$
, where
$O(\unicode[STIX]{x1D716})$
, where
 $\unicode[STIX]{x1D716}$
is the (small) Mach number of the acoustic waves, rather than at
$\unicode[STIX]{x1D716}$
is the (small) Mach number of the acoustic waves, rather than at
 $O(\unicode[STIX]{x1D716}^{2})$
, as in viscously driven Rayleigh streaming. In particular, the authors show that the
$O(\unicode[STIX]{x1D716}^{2})$
, as in viscously driven Rayleigh streaming. In particular, the authors show that the
 $O(\unicode[STIX]{x1D716})$
baroclinic streaming flow is sufficiently strong to induce
$O(\unicode[STIX]{x1D716})$
baroclinic streaming flow is sufficiently strong to induce
 $O(1)$
rearrangements of the background temperature and density fields, resulting in a two-way coupled system for the acoustic waves and the mean flow. These large variations in the background density field modify the spatial structure, natural frequency and amplitude of the acoustic mode on the streaming time scale. Notably, the two-way coupling precludes a sequential solution of the governing equations (the usual approach in one-way coupled streaming), seemingly necessitating the use of prohibitively expensive direct numerical simulations (DNS). This numerical challenge is elegantly circumvented by the authors via the derivation of a novel amplitude equation which allows for the computation of the streaming flow without evolving the sound waves over the fast temporal scale. Their formulation represents a significant advancement in the field since it enables inexpensive numerical simulations over several thousand acoustic-wave periods, a challenging feat for direct numerical simulations even by modern computational standards.
$O(1)$
rearrangements of the background temperature and density fields, resulting in a two-way coupled system for the acoustic waves and the mean flow. These large variations in the background density field modify the spatial structure, natural frequency and amplitude of the acoustic mode on the streaming time scale. Notably, the two-way coupling precludes a sequential solution of the governing equations (the usual approach in one-way coupled streaming), seemingly necessitating the use of prohibitively expensive direct numerical simulations (DNS). This numerical challenge is elegantly circumvented by the authors via the derivation of a novel amplitude equation which allows for the computation of the streaming flow without evolving the sound waves over the fast temporal scale. Their formulation represents a significant advancement in the field since it enables inexpensive numerical simulations over several thousand acoustic-wave periods, a challenging feat for direct numerical simulations even by modern computational standards.
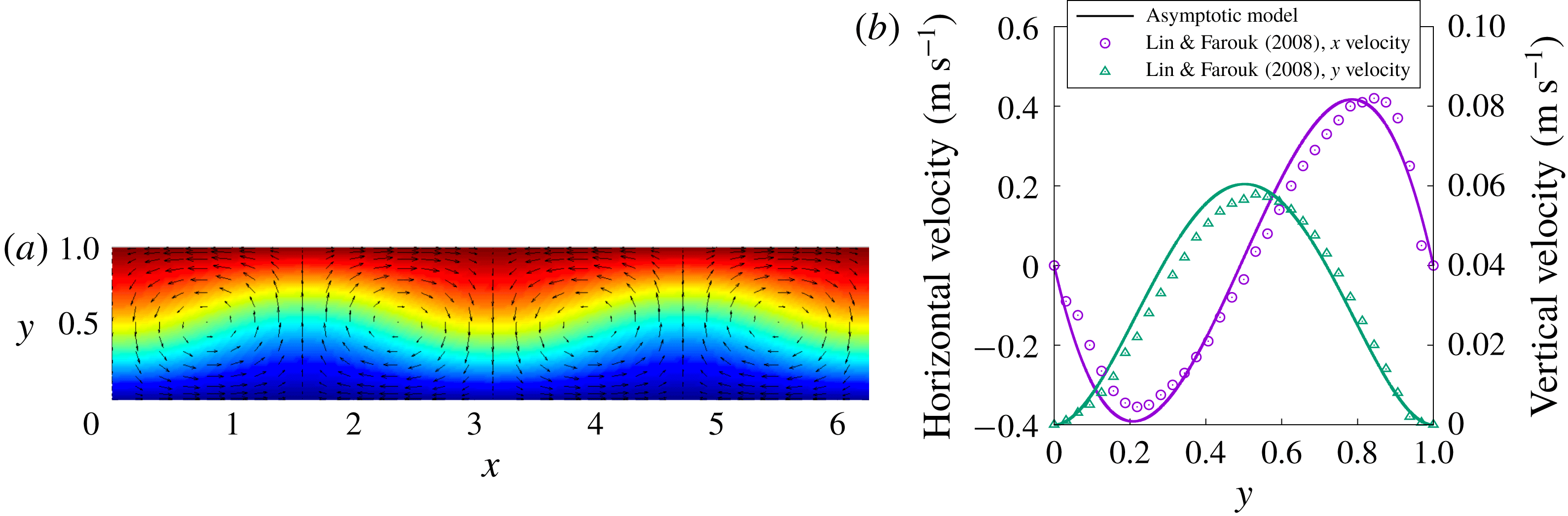
The authors then use their new algorithm to investigate phenomenology, demonstrating that even for comparably weak acoustic forcing, baroclinic streaming differs significantly from Rayleigh streaming, both in intensity and in spatial structure. In particular, baroclinic streaming results in much faster mean flows and, as first observed in the DNS of Lin & Farouk (Reference Lin and Farouk2008), upon imposition of a cross-channel temperature differential the streaming vortices span the channel width (see figure 2); in contrast, in Rayleigh streaming, the cells are stacked in the wall-normal direction. For both reasons, baroclinic streaming also enhances cross-channel heat transport in comparison to classical boundary-layer-driven acoustic streaming. As evident in figure 2, the mean flow computed via the authors’ asymptotic formalism exhibits excellent quantitative agreement with the streaming extracted from full DNS (Lin & Farouk Reference Lin and Farouk2008). For stronger acoustic forcing, further remarkable variations of the streaming flow are revealed. Specifically, as the amplitude of the acoustic wave is increased, the mid-plane symmetry along the channel height is broken and narrow jet-like flow structures are observed (see the title image). Moreover, the Nusselt number
 $Nu$
scales with the fourth power of the acoustic-wave amplitude, leading to significantly increased heat transport for large wave amplitudes.
$Nu$
scales with the fourth power of the acoustic-wave amplitude, leading to significantly increased heat transport for large wave amplitudes.
Figure 2. Steady-state baroclinic acoustic streaming velocity (vector arrows) and total temperature (colour) fields (left) for a parameter regime corresponding to the DNS of Lin & Farouk (Reference Lin and Farouk2008). Unlike classical boundary-layer-driven (Rayleigh) streaming, the cells span the channel. The asymptotic formulation enables the quantitative prediction of the streaming speeds (right) and pattern without the need to temporally resolve the fast acoustic waves. Adapted from Michel & Chini (Reference Michel and Chini2019).
The key take-away messages for the readers can be summarized as follows: the presence of an inhomogeneous background density field strongly affects both the structure and intensity of acoustic streaming. This phenomenon occurs due to the baroclinic generation of wave vorticity even in the absence of viscous torques, resulting in enhanced momentum transfer from the waves to the streaming flow. In the limit of comparably weak acoustic forcing,
 $Nu$
is found to depend strongly on the non-dimensional channel height (i.e. to the eighth power!), suggesting that the acoustic-wave frequency should be tuned to maintain an aspect ratio of order unity for heat transfer enhancement applications. In the stronger forcing regime, the streaming is observed to transition into jet-like flow structures. Crucially, in both cases,
$Nu$
is found to depend strongly on the non-dimensional channel height (i.e. to the eighth power!), suggesting that the acoustic-wave frequency should be tuned to maintain an aspect ratio of order unity for heat transfer enhancement applications. In the stronger forcing regime, the streaming is observed to transition into jet-like flow structures. Crucially, in both cases,
 $Nu$
is independent of
$Nu$
is independent of
 $\unicode[STIX]{x1D716}$
, while in Rayleigh streaming
$\unicode[STIX]{x1D716}$
, while in Rayleigh streaming
 $Nu=O(\unicode[STIX]{x1D716}^{2})$
. Finally, an exciting contribution of this study lies in the derivation of an amplitude equation that enables a temporal multiscale system to be reduced to a dynamical system evolving strictly on a slow time scale.
$Nu=O(\unicode[STIX]{x1D716}^{2})$
. Finally, an exciting contribution of this study lies in the derivation of an amplitude equation that enables a temporal multiscale system to be reduced to a dynamical system evolving strictly on a slow time scale.
3 Outlook and future directions
The study by Michel & Chini (Reference Michel and Chini2019), in combination with previous reports (Dreeben & Chini Reference Dreeben and Chini2011; Chini et al.
Reference Chini, Malecha and Dreeben2014), identifies a fundamentally and technologically important class of baroclinically driven acoustic streaming flows. In the future, carefully designed and well-controlled experiments in stably stratified fluids can be attempted to enable both quantitative assessment of the current formulation as well as its further development. Further extension of the formulation to treat channels of arbitrary aspect ratio will allow for even broader applicability and enable the investigation of novel applications.
In closing, the formalism developed by Michel & Chini (Reference Michel and Chini2019) for studying the interaction of acoustic waves with a stratified fluid represents an important contribution to the field of acoustic streaming with wide-ranging applications such as enhanced mixing at microscales, performance optimization of high-intensity discharge lamps and cooling of electronics aboard spacecraft, and suggests that prior studies of streaming-induced heat transfer from immersed bodies may warrant re-analysis.
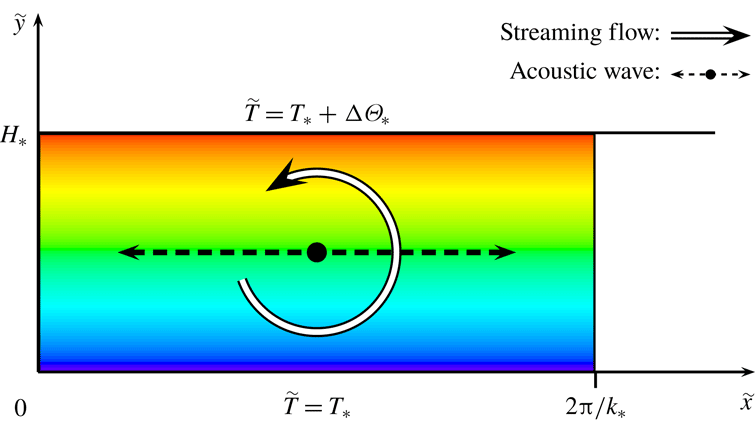
$H_{\ast }$. A standing acoustic wave of wavelength
$2\unicode[STIX]{x03C0}/k_{\ast }$ interacts with the thermal stratification to drive a time-mean, or streaming, flow that is sufficiently strong to modify the wave dynamics. The thermal driving is imposed by fixing the temperature
$\tilde{T}$ of the lower wall to be
$T_{\ast }$ and that of the upper wall to be
$T_{\ast }+\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}_{\ast }$. Adapted from Michel & Chini (2019).



1 Introduction
Steady streaming, i.e. the generation of a mean flow in a fluid upon periodic actuation, has been studied for nearly two centuries (Faraday Reference Faraday1831; Rayleigh Reference Rayleigh1884). Typically, the generation of steady streaming requires one of the following three ingredients: (i) the presence of an oscillatory non-conservative body force, (ii) viscous attenuation of the oscillatory motion resulting in Reynolds stress or (iii) the presence of an oscillating deformable boundary (Riley Reference Riley2001; Chini, Malecha & Dreeben Reference Chini, Malecha and Dreeben2014). Acoustic streaming is a sub-class of steady streaming in which the oscillatory actuation arises from high-frequency sound waves and is generally associated with scenario (ii), with viscous torques being the primary agency for the development of the fluctuating vorticity field. In most cases, the streaming flow is weaker than the driving oscillatory flow and produces no appreciable feedback on the wave dynamics, thereby rendering itself amenable to theoretical analysis via a perturbation expansion approach (Nyborg Reference Nyborg, Hamilton and Blackstock1998; Vanneste & Bühler Reference Vanneste and Bühler2011; Nama, Huang & Costanzo Reference Nama, Huang and Costanzo2017). However, large-amplitude streaming flows, with speeds comparable to those of the driving oscillatory flow, can be realized for cases where viscosity is not the primary source of fluctuating vorticity (Amin Reference Amin1988; Riley & Trinh Reference Riley and Trinh2001; Červenka & Bednařík Reference Červenka and Bednařík2017). This latter class of streaming involves a strong coupling between the oscillatory acoustic fields and the concomitant streaming flow, posing significant numerical challenges owing to the widely separated temporal scales of these two physical phenomena. Michel & Chini (Reference Michel and Chini2019) investigate this important class of acoustic streaming by mathematically reformulating the temporal multiscale system as a dynamical system evolving strictly on a single (i.e. the streaming) time scale.
2 Overview
The article by Michel & Chini (Reference Michel and Chini2019) systematically extends a previous analysis by Chini et al. (Reference Chini, Malecha and Dreeben2014) to investigate strong coupling between the oscillatory flow and the baroclinically generated acoustic streaming. To this end, they consider a two-dimensional flow of an ideal gas in a long, thin channel with the upper and lower walls maintained at fixed but differing temperatures; see figure 1. This represents an excellent choice of system for study since a thin channel dynamically constrains the acoustic wave to maintain its first-mode wall-normal structure, simplifying the analysis of the acoustic wave. Furthermore, this configuration ensures that the leading-order (wall-parallel) fluctuating pressure gradient is orthogonal to the imposed background density gradient, thereby yielding a crucial baroclinic contribution to the generation of fluctuating vorticity.
Figure 1. Schematic of the flow configuration. A thermally stratified ideal gas is confined between the plane parallel walls of a long thin channel of height $H_{\ast }$
. A standing acoustic wave of wavelength
$H_{\ast }$
. A standing acoustic wave of wavelength
 $2\unicode[STIX]{x03C0}/k_{\ast }$
interacts with the thermal stratification to drive a time-mean, or streaming, flow that is sufficiently strong to modify the wave dynamics. The thermal driving is imposed by fixing the temperature
$2\unicode[STIX]{x03C0}/k_{\ast }$
interacts with the thermal stratification to drive a time-mean, or streaming, flow that is sufficiently strong to modify the wave dynamics. The thermal driving is imposed by fixing the temperature
 $\tilde{T}$
of the lower wall to be
$\tilde{T}$
of the lower wall to be
 $T_{\ast }$
and that of the upper wall to be
$T_{\ast }$
and that of the upper wall to be
 $T_{\ast }+\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}_{\ast }$
. Adapted from Michel & Chini (Reference Michel and Chini2019).
$T_{\ast }+\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}_{\ast }$
. Adapted from Michel & Chini (Reference Michel and Chini2019).
A primary distinction between this work and earlier acoustic streaming studies is that the streaming flow arises at $O(\unicode[STIX]{x1D716})$
, where
$O(\unicode[STIX]{x1D716})$
, where
 $\unicode[STIX]{x1D716}$
is the (small) Mach number of the acoustic waves, rather than at
$\unicode[STIX]{x1D716}$
is the (small) Mach number of the acoustic waves, rather than at
 $O(\unicode[STIX]{x1D716}^{2})$
, as in viscously driven Rayleigh streaming. In particular, the authors show that the
$O(\unicode[STIX]{x1D716}^{2})$
, as in viscously driven Rayleigh streaming. In particular, the authors show that the
 $O(\unicode[STIX]{x1D716})$
baroclinic streaming flow is sufficiently strong to induce
$O(\unicode[STIX]{x1D716})$
baroclinic streaming flow is sufficiently strong to induce
 $O(1)$
rearrangements of the background temperature and density fields, resulting in a two-way coupled system for the acoustic waves and the mean flow. These large variations in the background density field modify the spatial structure, natural frequency and amplitude of the acoustic mode on the streaming time scale. Notably, the two-way coupling precludes a sequential solution of the governing equations (the usual approach in one-way coupled streaming), seemingly necessitating the use of prohibitively expensive direct numerical simulations (DNS). This numerical challenge is elegantly circumvented by the authors via the derivation of a novel amplitude equation which allows for the computation of the streaming flow without evolving the sound waves over the fast temporal scale. Their formulation represents a significant advancement in the field since it enables inexpensive numerical simulations over several thousand acoustic-wave periods, a challenging feat for direct numerical simulations even by modern computational standards.
$O(1)$
rearrangements of the background temperature and density fields, resulting in a two-way coupled system for the acoustic waves and the mean flow. These large variations in the background density field modify the spatial structure, natural frequency and amplitude of the acoustic mode on the streaming time scale. Notably, the two-way coupling precludes a sequential solution of the governing equations (the usual approach in one-way coupled streaming), seemingly necessitating the use of prohibitively expensive direct numerical simulations (DNS). This numerical challenge is elegantly circumvented by the authors via the derivation of a novel amplitude equation which allows for the computation of the streaming flow without evolving the sound waves over the fast temporal scale. Their formulation represents a significant advancement in the field since it enables inexpensive numerical simulations over several thousand acoustic-wave periods, a challenging feat for direct numerical simulations even by modern computational standards.
The authors then use their new algorithm to investigate phenomenology, demonstrating that even for comparably weak acoustic forcing, baroclinic streaming differs significantly from Rayleigh streaming, both in intensity and in spatial structure. In particular, baroclinic streaming results in much faster mean flows and, as first observed in the DNS of Lin & Farouk (Reference Lin and Farouk2008), upon imposition of a cross-channel temperature differential the streaming vortices span the channel width (see figure 2); in contrast, in Rayleigh streaming, the cells are stacked in the wall-normal direction. For both reasons, baroclinic streaming also enhances cross-channel heat transport in comparison to classical boundary-layer-driven acoustic streaming. As evident in figure 2, the mean flow computed via the authors’ asymptotic formalism exhibits excellent quantitative agreement with the streaming extracted from full DNS (Lin & Farouk Reference Lin and Farouk2008). For stronger acoustic forcing, further remarkable variations of the streaming flow are revealed. Specifically, as the amplitude of the acoustic wave is increased, the mid-plane symmetry along the channel height is broken and narrow jet-like flow structures are observed (see the title image). Moreover, the Nusselt number $Nu$
scales with the fourth power of the acoustic-wave amplitude, leading to significantly increased heat transport for large wave amplitudes.
$Nu$
scales with the fourth power of the acoustic-wave amplitude, leading to significantly increased heat transport for large wave amplitudes.
Figure 2. Steady-state baroclinic acoustic streaming velocity (vector arrows) and total temperature (colour) fields (left) for a parameter regime corresponding to the DNS of Lin & Farouk (Reference Lin and Farouk2008). Unlike classical boundary-layer-driven (Rayleigh) streaming, the cells span the channel. The asymptotic formulation enables the quantitative prediction of the streaming speeds (right) and pattern without the need to temporally resolve the fast acoustic waves. Adapted from Michel & Chini (Reference Michel and Chini2019).
The key take-away messages for the readers can be summarized as follows: the presence of an inhomogeneous background density field strongly affects both the structure and intensity of acoustic streaming. This phenomenon occurs due to the baroclinic generation of wave vorticity even in the absence of viscous torques, resulting in enhanced momentum transfer from the waves to the streaming flow. In the limit of comparably weak acoustic forcing, $Nu$
is found to depend strongly on the non-dimensional channel height (i.e. to the eighth power!), suggesting that the acoustic-wave frequency should be tuned to maintain an aspect ratio of order unity for heat transfer enhancement applications. In the stronger forcing regime, the streaming is observed to transition into jet-like flow structures. Crucially, in both cases,
$Nu$
is found to depend strongly on the non-dimensional channel height (i.e. to the eighth power!), suggesting that the acoustic-wave frequency should be tuned to maintain an aspect ratio of order unity for heat transfer enhancement applications. In the stronger forcing regime, the streaming is observed to transition into jet-like flow structures. Crucially, in both cases,
 $Nu$
is independent of
$Nu$
is independent of
 $\unicode[STIX]{x1D716}$
, while in Rayleigh streaming
$\unicode[STIX]{x1D716}$
, while in Rayleigh streaming
 $Nu=O(\unicode[STIX]{x1D716}^{2})$
. Finally, an exciting contribution of this study lies in the derivation of an amplitude equation that enables a temporal multiscale system to be reduced to a dynamical system evolving strictly on a slow time scale.
$Nu=O(\unicode[STIX]{x1D716}^{2})$
. Finally, an exciting contribution of this study lies in the derivation of an amplitude equation that enables a temporal multiscale system to be reduced to a dynamical system evolving strictly on a slow time scale.
3 Outlook and future directions
The study by Michel & Chini (Reference Michel and Chini2019), in combination with previous reports (Dreeben & Chini Reference Dreeben and Chini2011; Chini et al. Reference Chini, Malecha and Dreeben2014), identifies a fundamentally and technologically important class of baroclinically driven acoustic streaming flows. In the future, carefully designed and well-controlled experiments in stably stratified fluids can be attempted to enable both quantitative assessment of the current formulation as well as its further development. Further extension of the formulation to treat channels of arbitrary aspect ratio will allow for even broader applicability and enable the investigation of novel applications.
In closing, the formalism developed by Michel & Chini (Reference Michel and Chini2019) for studying the interaction of acoustic waves with a stratified fluid represents an important contribution to the field of acoustic streaming with wide-ranging applications such as enhanced mixing at microscales, performance optimization of high-intensity discharge lamps and cooling of electronics aboard spacecraft, and suggests that prior studies of streaming-induced heat transfer from immersed bodies may warrant re-analysis.