Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-24T06:00:59.442Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimal-energy perturbations rapidly approaching the edge state in Couette flow

Published online by Cambridge University Press:  20 January 2015

S. Cherubini  and
P. De Palma
S. Cherubini*
Affiliation:
DynFluid, Arts et Metiers ParisTech, 151, Boulevard de l’Hopital, 75013 Paris, France
P. De Palma
Affiliation:
DMMM and CEMeC, Politecnico di Bari, via Re David 200, 70125 Bari, Italy
*
†Email address for correspondence: s.cherubini@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Transition to turbulence in shear flows is often subcritical, thus the dynamics of the flow strongly depends on the shape and amplitude of the perturbation of the laminar state. In the state space, initial perturbations which directly relaminarize are separated from those that go through a chaotic trajectory by a hypersurface having a very small number of unstable dimensions, known as the edge of chaos. Even for the simple case of plane Couette flow in a small domain, the edge of chaos is characterized by a fractal, folded structure. Thus, the problem of determining the threshold energy to trigger subcritical transition consists in finding the states on this complex hypersurface with minimal distance (in the energy norm) from the laminar state. In this work we have investigated the minimal-energy regions of the edge of chaos, by developing a minimization method looking for the minimal-energy perturbations capable of approaching the edge state (within a prescribed tolerance) in a finite target time 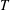$T$. For sufficiently small target times, the value of the minimal energy has been found to vary with 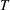$T$ following a power law, whose best fit is given by 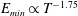$E_{min}\propto T^{-1.75}$. For large values of 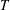$T$, the minimal energy achieves a constant value which corresponds to the energy of the minimal seed, namely the perturbation of minimal energy asymptotically approaching the edge state (Rabin et al., J. Fluid Mech., vol. 738, 2012, R1). For 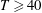$T\geqslant 40$, all of the symmetries of the edge state are broken and the minimal perturbation appears to be localized in space with a basic structure composed of scattered patches of streamwise velocity with inclined streamwise vortices on their flanks. Finally, we have found that minimal perturbations originate in a small low-energy zone of the state space and follow very fast similar trajectories towards the edge state. Such trajectories are very different from those of linear optimal disturbances, which need much higher initial amplitudes to approach the edge state. The time evolution of these minimal perturbations represents the most efficient path to subcritical transition for Couette flow.

JFM classification

Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Instability: Nonlinear instability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 764 , 10 February 2015 , pp. 572 - 598
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, K., Moxey, D., de Lozar, A., Avila, M., Barkley, D. & Hof, B. 2011 The onset of turbulence in pipe flow. Science 333, 192–196.CrossRefGoogle ScholarPubMed
Bottin, S. & Chaté, H. 1998 Statistical analysis of the transition to turbulence in plane Couette flow. Eur. Phys. J. B 6, 143–155.CrossRefGoogle Scholar
Bottin, S., Daviaud, F., Manneville, P. & Dauchot, O. 1998 Discontinuous transition to spatiotemporal intermittency in plane Couette flow. Europhys. Lett. 43, 171–176.CrossRefGoogle Scholar
Chantry, M. & Schneider, T. M. 2014 Studying edge geometry in transiently turbulent shear flows. J. Fluid Mech. 747, 506–517.CrossRefGoogle Scholar
Cherubini, S. & De Palma, P. 2013 Nonlinear optimal perturbations in a Couette flow: bursting and transition. J. Fluid Mech. 716, 251–279.CrossRefGoogle Scholar
Cherubini, S., De Palma, P., Robinet, J. C. & Bottaro, A. 2010a Rapid path to transition via non-linear localized optimal perturbations in a boundary-layer flow. Phys. Rev. E 82, 066302.CrossRefGoogle Scholar
Cherubini, S., De Palma, P., Robinet, J. C. & Bottaro, A. 2011 The minimal seed of turbulent transition in a boundary layer. J. Fluid Mech. 689, 221–253.CrossRefGoogle Scholar
Cherubini, S., Robinet, J. C., Bottaro, A. & De Palma, P. 2011 Optimal wave packets in a boundary layer and initial phases of a turbulent spot. J. Fluid Mech. 656, 231–259.CrossRefGoogle Scholar
Cherubini, S., Robinet, J.-C. & De Palma, P. 2010c The effects of non-normality and non-linearity of the Navier–Stokes operator on the dynamics of a large laminar separation bubble. Phys. Fluids 22 (1), 014102.CrossRefGoogle Scholar
Cossu, C. 2005 An optimality condition on the minimum energy threshold in subcritical instabilities. C. R. Méc 333, 331–336.CrossRefGoogle Scholar
Cossu, C., Brandt, L., Bagheri, S. & Henningson, D. S. 2011 Secondary threshold amplitudes for sinuous streak breakdown. Phys. Fluids 23, 074103.CrossRefGoogle Scholar
Dauchot, O. & Daviaud, F. 1995 Finite amplitude perturbation and spots growth mechanism in plane Couette flow. Phys. Fluids 7, 335–343.CrossRefGoogle Scholar
Duguet, Y., Brandt, L. & Larsson, B. R. J. 2010 Towards minimal perturbations in transitional plane Couette flow. Phys. Rev. E 82, 026316.CrossRefGoogle ScholarPubMed
Duguet, Y., Monokrousos, A., Brandt, L. & Henningson, D. S. 2013 Minimal transition thresholds in plane Couette flow. Phys. Fluids 25, 084103.CrossRefGoogle Scholar
Eckhardt, B., Schneider, T. M., Hof, B. & Westerweel, J. 2007 Turbulence transition of pipe flow. Annu. Rev. Fluid Mech. 39, 447–468.CrossRefGoogle Scholar
Ehrenstein, U. & Gallaire, F. 2005 On two-dimensional temporal modes in spatially evolving open flows: the flat-plate boundary layer. J. Fluid Mech. 536, 209–218.CrossRefGoogle Scholar
Farrell, B. 1988 Optimal excitation of perturbations in viscous shear flow. Phys. Fluids 31, 2093–2102.CrossRefGoogle Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2009 Equilibrium and traveling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 243–266.CrossRefGoogle Scholar
Hof, B., Westerweel, J., Schneider, T. M. & Eckhardt, B. 2006 Finite lifetime of turbulence in shear flows. Nature 443, 59–62.CrossRefGoogle ScholarPubMed
Itano, T. & Toh, S. 2001 The dynamics of bursting process in wall turbulence. J. Phys. Soc. 70, 703–716.CrossRefGoogle Scholar
Kerswell, R. & Tutty, R. O. 2007 Recurrence of travelling waves in transitional pipe flows. J. Fluid Mech. 584, 69–101.CrossRefGoogle Scholar
Kreilos, T. & Eckhardt, B. 2012 Periodic orbit near onset of chaos in plane Couette flow. Chaos: An Interdisciplinary Journal of Nonlinear Science 22, 047505.CrossRefGoogle ScholarPubMed
Lai, Y.-C. & Tél, T. 2011 Transient Chaos. Springer.CrossRefGoogle Scholar
Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98, 243–251.CrossRefGoogle Scholar
Lebovitz, N. 2009 Shear-flow transition: the basin boundary. Nonlinearity 22, 2645–2655.CrossRefGoogle Scholar
Lebovitz, N. & Mariotti, G. 2013 Edges in models of shear flow. J. Fluid Mech. 721, 386–402.CrossRefGoogle Scholar
Monokrousos, A., Bottaro, A., Brandt, L., Di Vita, A. & Henningson, D. S. 2011 Non-equilibrium thermodynamics and the optimal path to turbulence in shear flows. Phys. Rev. Lett. 106, 134502.CrossRefGoogle Scholar
Nagata, M. 1990 Three-dimensional finite amplitude solutions in plane Couette flow. J. Fluid Mech. 217, 519–527.CrossRefGoogle Scholar
Orr, W. M. 1907 The stability or instability of the steady motions of a liquid. Part I. Proc. R. Irish Acad. A 27, 9–68.Google Scholar
Ott, E. 2002 Chaos in Dynamical Systems. Cambridge University Press.CrossRefGoogle Scholar
Pringle, C. C. T. & Kerswell, R. R. 2010 Using nonlinear transient growth to construct the minimal seed for shear flow turbulence. Phys. Rev. Lett. 105, 154502.CrossRefGoogle ScholarPubMed
Pringle, C. C. T., Willis, A. P. & Kerswell, R. R. 2012 Minimal seeds for shear flow turbulence: using nonlinear transient growth to touch the edge of chaos. J. Fluid Mech. 702, 415–443.CrossRefGoogle Scholar
Pyragas, K. 1992 Continuous control of chaos by self-controlling feedback. Phys. Lett. A 170, 421–428.CrossRefGoogle Scholar
Rabin, S. M. E., Caulfield, C. P. & Kerswell, R. R. 2012 Triggering turbulence efficiently in plane Couette flow. J. Fluid Mech. 712, 244–272.CrossRefGoogle Scholar
Rabin, S. M. E., Caulfield, C. P. & Kerswell, R. R. 2014 Designing a more nonlinearly stable laminar flow via boundary manipulation. J. Fluid Mech. 738, R1.CrossRefGoogle Scholar
Reddy, S. C., Schmid, P. J., Baggett, J. S. & Henningson, D. S. 1998 On stability of streamwise streaks and transition thresholds in plane channel flows. J. Fluid Mech. 365, 269–303.CrossRefGoogle Scholar
Reynolds, O. 1883 An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channel. Phil. Trans. R. Soc. Lond. A 174, 935–982.Google Scholar
Romanov, V. A. 1973 Stability of plane-parallel Couette flow. Funct. Anal. Applics. 7, 137–146.CrossRefGoogle Scholar
Schmiegel, A. & Eckhardt, B. 1997 Fractal stability border in plane Couette flow. Phys. Rev. Lett. 79, 5250–5253.CrossRefGoogle Scholar
Schneider, T. M., De Lillo, F., Buehrle, J., Eckhardt, B., Dörnemann, T., Dörnemann, K. & Freisleben, B. 2010 Transient turbulence in plane Couette flow. Phys. Rev. E 81, 015301(R).CrossRefGoogle ScholarPubMed
Schneider, T. M. & Eckhardt, B. 2006 Edge of chaos in pipe flow. Chaos: An Interdisciplinary Journal of Nonlinear Science 16, 041103.CrossRefGoogle ScholarPubMed
Schneider, T. M., Gibson, J. F., Lagha, M., De Lillo, F. & Eckhardt, B. 2008 Laminar–turbulent boundary in plane Couette flow. Phys. Rev. E 78, 037301.CrossRefGoogle ScholarPubMed
Skufca, J. D., Yorke, J. A. & Eckhardt, B. 2006 Edge of chaos in a parallel shear flow. Phys. Rev. Lett. 96, 174101.CrossRefGoogle Scholar
Tasaka, Y., Schneider, T. M. & Mullin, T. 2010 Folded edge of turbulence in a pipe. Phys. Rev. Lett. 105, 174502.CrossRefGoogle Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for the three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123 (2), 402–414.CrossRefGoogle Scholar
Vollmer, J., Schneider, T. M. & Eckhardt, B. 2009 Basin boundary, edge of chaos and edge state in a two-dimensional model. New J. Phys. 11, 013040.CrossRefGoogle Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–901.CrossRefGoogle Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 15, 1517–1534.CrossRefGoogle Scholar
Wang, J., Gibson, J. F. & Waleffe, F. 2007 Lower branch coherent states: transition and control. Phys. Rev. Lett. 98, 204501.CrossRefGoogle ScholarPubMed