Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-23T06:26:32.866Z Has data issue: false hasContentIssue false
  • English
  • Français

The minimal seed of turbulent transition in the boundary layer

Published online by Cambridge University Press:  15 November 2011

S. Cherubini ,
P. De Palma ,
J.-C. Robinet  and
A. Bottaro
S. Cherubini*
Affiliation:
DIMeG, CEMeC, Politecnico di Bari, Via Re David 200, 70125 Bari, Italy
P. De Palma
Affiliation:
DIMeG, CEMeC, Politecnico di Bari, Via Re David 200, 70125 Bari, Italy
J.-C. Robinet
Affiliation:
DynFluid Laboratory, Arts et Metiers ParisTech, 151 Boulevard de l’Hopital, 75013 Paris, France
A. Bottaro
Affiliation:
DICAT, Università di Genova, Via Montallegro 1, 16145 Genova, Italy
*
†Email address for correspondence: s.cherubini@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper describes a scenario of transition from laminar to turbulent flow in a spatially developing boundary layer over a flat plate. The base flow is the Blasius non-parallel flow solution; it is perturbed by optimal disturbances yielding the largest energy growth over a short time interval. Such perturbations are computed by a nonlinear global optimization approach based on a Lagrange multiplier technique. The results show that nonlinear optimal perturbations are characterized by a localized basic building block, called the minimal seed, defined as the smallest flow structure which maximizes the energy growth over short times. It is formed by vortices inclined in the streamwise direction surrounding a region of intense streamwise disturbance velocity. Such a basic structure appears to be a robust feature of the base flow since it is practically invariant with respect to the initial energy of the perturbation, the target time, the Reynolds number and the dimensions of the computational domain. The minimal seed grows very rapidly in time while spreading, and it triggers nonlinear effects which bring the flow to turbulence in a very efficient manner, through the formation of a turbulence spot. This evolution of the initial optimal disturbance has been studied in detail by direct numerical simulations. Using a perturbative formulation of the Navier–Stokes equations, each linear and nonlinear convective term of the equations has been analysed. The results show the fundamental role of the streamwise inclination of the vortices in the process. The nonlinear coupling of the finite amplitude disturbances is crucial to sustain such streamwise inclination, as well as to generate dislocations within the flow structures, and local inflectional velocity distributions. The analysis provides a picture of the transition process characterized by a sequence of structures appearing successively in the flow, namely, 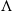vortices, hairpin vortices and streamwise streaks. Finally, a disturbance regeneration cycle is conceived, initiated by the fast nonlinear amplification of the minimal seed, providing a possible scenario for the continuous regeneration of the same fundamental flow structures at smaller space and time scales.

JFM classification

Boundary Layers: Boundary layer stability Instability: Nonlinear instability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 689 , 25 December 2011 , pp. 221 - 253
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.CrossRefGoogle Scholar
2. Berlin, S., Lundbladh, A. & Henningson, D. S. 1994 Spatial simulations of oblique transition in a boundary layer. Phys. Fluids 6, 1–3 , 1949.CrossRefGoogle Scholar
3. Berlin, S., Wiegel, M. & Henningson, D. S. 1999 Numerical and experimental investigations of oblique boundary layer transition. J. Fluid Mech. 393, 23–57.Google Scholar
4. Biau, D. & Bottaro, A. 2009 An optimal path to transition in a duct. Phil. Trans. R. Soc. A 367, 529–544.CrossRefGoogle Scholar
5. Bottaro, A. 1990 Note on open boundary conditions for elliptic flows. Numer. Heat Transfer B 18, 243–256.Google Scholar
6. Bottaro, A. 1993 On longitudinal vortices in curved channel flow. J. Fluid Mech. 251, 627–660.Google Scholar
7. Brandt, L., Schlatter, P. & Henningson, D. S. 2004 Transition in a boundary layers subject to free stream turbulence. J. Fluid Mech. 517, 167–198.CrossRefGoogle Scholar
8. Cherubini, S., De Palma, P., Robinet, J.-Ch. & Bottaro, A. 2010a Rapid path to transition via nonlinear localized optimal perturbations. Phys. Rev. E 82, 066302.CrossRefGoogle ScholarPubMed
9. Cherubini, S., De Palma, P., Robinet, J.-Ch. & Bottaro, A. 2011 Edge states in a boundary layer. Phys. Fluids 23, 051705.Google Scholar
10. Cherubini, S., Robinet, J.-Ch., Bottaro, A. & De Palma, P. 2010b Optimal wave packets in a boundary layer and initial phases of a turbulent spot. J. Fluid Mech. 656, 231–259.Google Scholar
11. Chomaz, J. M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.CrossRefGoogle Scholar
12. Corbett, P. & Bottaro, A. 2000 Optimal perturbations for boundary layers subject to stream-wise pressure gradient. Phys. Fluids 12, 120–130.CrossRefGoogle Scholar
13. Corino, E. R. & Brodkey, R. S. 1969 A visual investigation of the wall region in turbulent flow. J. Fluid Mech. 37, 1.CrossRefGoogle Scholar
14. Duguet, Y., Brandt, L. & Larsson, B. R. J. 2010 Towards minimal perturbations in transitional plane Couette flow. Phys. Rev. E 82, 026316.CrossRefGoogle ScholarPubMed
15. Duguet, Y., Schlatter, P. & Henningson, D. 2009 Localized edge states in plane Couette flow. Phys. Fluids 21, 111701.CrossRefGoogle Scholar
16. Eckhardt, B., Schneider, T. M., Hof, B. & Westerweel, J. 2007 Turbulence transition of pipe flow. Annu. Rev. Fluid Mech. 39, 447–468.CrossRefGoogle Scholar
17. Faisst, H. & Eckhardt, B. 2003 Travelling waves in pipe flow. Phys. Rev. Lett. 91, 224502.CrossRefGoogle ScholarPubMed
18. Farrell, B. 1988 Optimal excitation of perturbations in viscous shear flow. Phys. Fluids 31, 2093–2102.CrossRefGoogle Scholar
19. Gibson, J. F., Halcrow, J. & Cvitanović, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 243.CrossRefGoogle Scholar
20. Guo, Y. & Finlay, W. H. 1991 Splitting, merging and wave length selection of vortices in curved and/or rotating channel flow due to Eckhaus instability. J. Fluid Mech. 228, 661–691.Google Scholar
21. Hof, B., van Doorne, C. W. H., Westerweel, J., Nieuwstadt, F. T. M., Faisst, H., Eckhardt, B., Wedin, H., Kerswell, R. R. & Waleffe, F. 2004 Experimental observation of nonlinear traveling waves in turbulent pipe flow. Science 305, 1594–1598.Google Scholar
22. Hunt, J. C. R., Wray, A. & Moin, P. 1988 Eddies, stream, and convergence zones in turbulent flows. Report CTR-S88, Center for Turbulence Research.Google Scholar
23. Jacobs, R. G. & Durbin, P. A. 2001 Simulations of bypass transition. J. Fluid Mech. 428, 185–212.CrossRefGoogle Scholar
24. Kawahara, G. & Kida, S. 2001 Periodic motion embedded in plane Couette turbulence: regeneration cycle and burst. J. Fluid Mech. 449, 291–300.CrossRefGoogle Scholar
25. Kline, S. J., Reynold, W. C., Schraub, F. & Rundstander, P. W. 1967 The structure of turbulent boundary layer flows. J. Fluid Mech. 30, 741–773.CrossRefGoogle Scholar
26. Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98, 243–251.Google Scholar
27. Luchini, P. 2000 Reynolds number indipendent instability of the Blasius boundary layer over a flat surface: optimal perturbations. J. Fluid Mech. 404, 289–309.CrossRefGoogle Scholar
28. Marquet, O., Sipp, D., Chomaz, J.-M. & Jacquin, L. 2008 Amplifier and resonator dynamics of a low-Reynolds-number recirculation bubble in a global framework. J. Fluid Mech. 605, 429–443.CrossRefGoogle Scholar
29. Mellibovsky, F., Meseguer, A., Schneider, T. M. & Eckhardt, B. 2009 Transition in localized pipe-flow turbulence. Phys. Rev. Lett. 103, 054502.CrossRefGoogle ScholarPubMed
30. Monokrousos, A., Akervik, E., Brandt, L. & Henningson, D. S. 2010 Global three-dimensional optimal disturbances in the Blasius boundary-layer flow using time steppers. J. Fluid Mech. 650, 181–214.Google Scholar
31. Monokrousos, A., Bottaro, A., Brandt, L., Di Vita, A. & Henningson, D. S. 2011 Non-equilibrium thermodynamics and the optimal path to turbulence in shear flows. Phys. Rev. Lett. 106, 134502.Google Scholar
32. Nagata, M. 1990 Three-dimensional finite amplitude solutions in plane Couette flow. J. Fluid Mech. 217, 519–527.CrossRefGoogle Scholar
33. Polak, E. & Ribière, G. 1969 Note sur la convergence de directions conjugées. Rev. Française Automat. Informat. Rech. Opér. 16, 35–43.Google Scholar
34. Pringle, C. C. T. & Kerswell, R. R. 2010 Using nonlinear transient growth to construct the minimal seed for shear flow turbulence. Phys. Rev. Lett. 105, 154502.CrossRefGoogle ScholarPubMed
35. Reddy, S. C., Schmid, P., Baggett, P. & Henningson, D. S. 1998 On stability of streamwise streaks and transition thresholds in plane channel flows. J. Fluid Mech. 365, 269–303.CrossRefGoogle Scholar
36. Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601.Google Scholar
37. Saric, W. S., Reed, H. J. & Kerschen, E. 2002 Boundary-layer receptivity to free stream disturbances. Annu. Rev. Fluid Mech. 34, 291–319.CrossRefGoogle Scholar
38. Schmid, P. & Henningson, D. 2001 Stability and Transition in Shear Fows. Springer.Google Scholar
39. Schneider, T. M., Eckhardt, B. & Yorke, J. A. 2007 Turbulence transition and the edge of chaos in pipe flow. Phys. Rev. Lett. 99, 034502.CrossRefGoogle ScholarPubMed
40. Schneider, T. M., Gibson, J. F. & Burke, J. 2010a Snakes and ladders: localized solutions of plane Couette flow. Phys. Rev. Lett. 104, 104501.Google Scholar
41. Schneider, T. M., Marinc, D. & Eckhardt, B. 2010b Localised edge states nucleate turbulence in extended plane Couette cells. J. Fluid Mech. 646, 441–451.Google Scholar
42. Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.CrossRefGoogle Scholar
43. Singer, B. A. 1996 Characteristics of a young turbulent spot. Phys. Fluids 8, 509–512.CrossRefGoogle Scholar
44. Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for the three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123 (2), 402–414.Google Scholar
45. Viswanath, D. & Cvitanovic, P. 2009 Stable manifolds and the transition to turbulence in pipe flow. J. Fluid Mech. 627, 215.CrossRefGoogle Scholar
46. Waleffe, F. 1995 Transition in shear flows: nonlinear normality versus non-normal linearity. Phys. Fluids 7, 3060–3066.Google Scholar
47. Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.CrossRefGoogle Scholar
48. Waleffe, F. 1998 Three-dimensional states in plane shear flow. Phys. Rev. Lett. 81, 4140–4143.CrossRefGoogle Scholar
49. Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.CrossRefGoogle Scholar
50. Westin, K. J. A., Boiko, A. V., Klingmann, B. G. B., Kozlov, V. V. & Alfredsson, P. H. 1994 Experiments in a boundary layer subject to free stream turbulence Part I: boundary layer structure and receptivity. J. Fluid Mech. 281, 193–218.Google Scholar
51. Willmarth, W. W. & Lu, S. S. 1972 Structure of the Reynolds stress near the wall. J. Fluid Mech. 55, 65.CrossRefGoogle Scholar
52. Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally-zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.CrossRefGoogle Scholar
53. Zuccher, S., Luchini, P. & Bottaro, A. 2004 Algebraic growth in a blasius boundary layer: optimal and robust control by mean suction in the nonlinear regime. Eur. J. Mech. (B/Fluids) 513, 135–160.Google Scholar

Cherubini et al. supplementary movie

Overall transition process initiated by the minimal seed perturbation. Green isosurfaces indicate regions of high vorticity (Q-criterion), blue ones indicate low-momentum zones ($u'=-0.5$).

Download Cherubini et al. supplementary movie(Video)
Video 341.8 KB

Cherubini et al. supplementary movie

Overall transition process initiated by the minimal seed perturbation. Green isosurfaces indicate regions of high vorticity (Q-criterion), blue ones indicate low-momentum zones ($u'=-0.5$).

Download Cherubini et al. supplementary movie(Video)
Video 208.1 KB