Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-26T17:57:01.941Z Has data issue: false hasContentIssue false
  • English
  • Français

A long-wave estimation for the damping coefficient at a flat water–water vapour interface with a phase transition

Published online by Cambridge University Press:  26 April 2019

V. V. Konovalov Open the ORCID record for V. V. Konovalov [Opens in a new window]  and
T. P. Lyubimova Open the ORCID record for T. P. Lyubimova [Opens in a new window]
V. V. Konovalov
Affiliation:
Institute of Continuous Media Mechanics, the Ural Branch of RAS, Perm 614013, Russia
T. P. Lyubimova*
Affiliation:
Institute of Continuous Media Mechanics, the Ural Branch of RAS, Perm 614013, Russia
*
†Email address for correspondence: lubimova@psu.ru
Get access Rights & Permissions [Opens in a new window]

Abstract

Gravitational–capillary waves, arising in a system of thick layers of two aggregate states of a substance, are studied using the example of water and its vapour. Their initially flat interface is in hydrostatic and thermodynamic equilibrium at atmospheric pressure and the corresponding saturation temperature 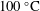$100\,^{\circ }\text{C}$, provided that a balance is maintained for heat fluxes transported through immovable phases in the process of heat conduction. From the problem of linear stability for small perturbations, estimation relations for their damping coefficient and eigenfrequency shift are obtained, including the factors of viscosities of the media and phase transition. The first two contributions, proportional to the kinematic viscosity of the liquid and the square root of the kinematic viscosity of its vapour, respectively, are consistent, accurate to additionally accounted for capillary forces, with the result of Dore’s analysis, which is a development of the weakly viscous Lamb theory for ‘deep water’. Numerical calculations have shown that, with increasing wavelength, the accuracy of the proposed approximation increases, especially for the wave damping coefficient, and the contribution of the viscosity of the light phase increases in percentage terms. As for the phase transition effect, which was previously overestimated using the quasi-equilibrium approximation, it remains insignificant at the level of heat fluxes acceptable in the model of thick layers of homogeneous media. The factor of thermocapillarity is found to be very weak; it becomes qualitatively noticeable only on the background of disappearing heating. Here, together with the factor of dependence of the saturation temperature on the phase pressure, it determines a non-zero correction to the wave damping coefficient.

JFM classification

Waves/Free-surface Flows: Capillary waves Phase change: Condensation/evaporation Multiphase and Particle-laden Flows: Gas/liquid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 869 , 25 June 2019 , pp. 417 - 438
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adham-Khodaparast, K., Kawaji, M. & Antar, B. N. 1995 The Rayleigh–Taylor and Kelvin–Helmholtz stability of a viscous liquid–vapor interface with heat and mass transfer. Phys. Fluids 7, 359–364.10.1063/1.868633Google Scholar
Antuono, M. & Colagrossi, A. 2013 The damping of viscous gravity waves. Wave Motion 50, 197–209.10.1016/j.wavemoti.2012.08.008Google Scholar
Awasthi, M. K. & Agrawal, G. S. 2011 Viscous potential flow analysis of Rayleigh–Taylor instability with heat and mass transfer. Intl J. Appl. Maths Mech. 7, 73–84.Google Scholar
Awasthi, M. K. 2013 Viscous corrections for the viscous potential flow analysis of Rayleigh–Taylor instability with heat and mass transfer. Trans. ASME J. Heat Transfer 135, 071701.10.1115/1.4023580Google Scholar
Badratinova, L. G., Colinet, P., Hennenberg, M. & Legros, J. C. 1996 On Rayleigh–Taylor instability in heated liquid–gas and liquid–vapour systems. Russ. J. Engng Thermophys. 6, 1–31.Google Scholar
Behroozi, F., Smith, J. & Even, W. 2010 Stokes’ dream: measurement of fluid viscosity from the attenuation of capillary waves. Am. J. Phys. 78, 1165–1169.10.1119/1.3467887Google Scholar
Berberan-Santos, M. N., Bodunov, E. N. & Pogliani, L. 2002 Liquid–vapor equilibrium in a gravitational field. Am. J. Phys. 70, 438–443.10.1119/1.1424264Google Scholar
Cerda, E. A. & Tirapegui, E. L. 1998 Faraday’s instability in viscous fluid. J. Fluid Mech. 368, 195–228.Google Scholar
Cherepanov, A. A. 1984 The influence of alternating external fields on the Rayleigh–Taylor instability. In Certain Problems of the Stability of a Liquid Surface (preprint), UNT’s AN SSSR. Ural Scientific Center, Academy of Sciences of the USSR, Sverdlovsk, (in Russian).Google Scholar
Delhaye, J. M., Giot, M. & Riethmuller, M. L. 1981 Thermohydraulics of Two-phase Systems for Industrial Design and Nuclear Engineering. MacGraw Hill.Google Scholar
Dore, B. D. 1969 A contribution to the theory of viscous damping of stratified wave flows. Acta Mech. 8, 25–33.10.1007/BF01178531Google Scholar
Dore, B. D. 1978 Some effects of the air–water interface on gravity waves. Geophys. Astrophys. Fluid Dyn. 10, 215–230.Google Scholar
Harrison, W. J. 1908 The influence of viscosity on the oscillations of superposed fluids. Proc. Lond. Math. Soc. S2–6, 396–405.10.1112/plms/s2-6.1.396Google Scholar
Ho, S.-P. 1980 Linear Rayleigh–Taylor stability of viscous fluids with mass and heat transfer. J. Fluid Mech. 101, 111–127.Google Scholar
Hsieh, D. Y. 1972 Effects of heat and mass transfer on Rayleigh–Taylor instability. Trans. ASME J. Basic Engng 94, 156–160.Google Scholar
Hsieh, D. Y. 1978 Interfacial stability with mass and heat transfer. Phys. Fluids 21, 745–748.Google Scholar
Hsieh, D. Y. 2003 On damping coefficient due to phase transformation. Acta Mech. Sin. 19, 204–207.10.1007/BF02484480Google Scholar
Hunt, N. 1964 The viscous damping of gravity waves in shallow water. La Houille Blanche 19, 685–691.10.1051/lhb/1964038Google Scholar
Ievlev, V. M. & Son, E. E. 1980 Stabilization of Rayleigh–Taylor instability of conducting liquid by the magnetic field and heat flux. Therm. Phys. High Temp. 18, 769–774 (in Russian).Google Scholar
Jeng, U.-S., Esibov, L., Crow, L. & Steyerl, A. 1998 Viscosity effect on capillary waves at liquid interfaces. J. Phys.: Condens. Matter 10, 4955–4962.Google Scholar
Jenkins, A. D. & Jacobs, S. J. 1997 Wave damping by a thin layer of viscous fluid. Phys. Fluids 9, 1256–1264.10.1063/1.869240Google Scholar
Johns, B. 1968 A boundary layer method for the determination of the viscous damping of small amplitude gravity waves. Q. J. Mech. Appl. Maths 21, 93–103.10.1093/qjmam/21.1.93Google Scholar
Joseph, D. D. & Wang, J. 2004 The dissipation approximation and viscous potential flow. J. Fluid Mech. 505, 365–377.10.1017/S0022112004008602Google Scholar
Kim, B. J. & Kim, K. D. 2016 Rayleigh–Taylor instability of viscous fluids with phase change. Phys. Rev. E 93, 043123.Google Scholar
Konovalov, V. V., Lyubimov, D. V. & Lyubimova, T. P. 2016 The Rayleigh–Taylor instability of the externally cooled liquid lying over a thin vapor film coating the wall of a horizontal plane heater. Phys. Fluids 28, 064102.10.1063/1.4952998Google Scholar
Konovalov, V. V., Lyubimov, D. V. & Lyubimova, T. P. 2017 Influence of phase transition on the instability of a liquid–vapour interface in a gravitational field. Phys. Rev. Fluids 2, 063902.Google Scholar
Kumar, K. & Tuckerman, L. S. 1994 Parametric instability of the interface between two fluids. J. Fluid Mech. 279, 49–68.10.1017/S0022112094003812Google Scholar
Lamb, H. 1895 Hydrodynamics, 2th edn. Cambridge University Press.Google Scholar
Lee, K. Y., Chou, T., Chug, D. S. & Mazur, E. 1993 Direct measurement of the spatial damping of capillary waves at liquid–vapour interfaces. J. Phys. Chem. 97, 12876–12878.10.1021/j100151a039Google Scholar
Lobov, N. I., Lyubimov, D. V. & Lyubimova, T. P. 1996 Convective instability of a system of horizontal layers of inmiscible liquids with a deformable interfaces. Fluid Dyn. 31, 186–192.10.1007/BF02029677Google Scholar
Lyubimov, D. V., Lyubimova, T. P. & Cherepanov, A. A. 2003 Dynamics of Interfaces in Vibrational Fields. Fizmatlit (in Russian).Google Scholar
Martel, C. & Knobloch, E. 1997 Damping of nearly inviscid water waves. Phys. Rev. E 56, 5544–5548.Google Scholar
Nevolin, V. G. 1977 Parametric excitation of waves at an interface. Fluid Dyn. 12, 302–305.Google Scholar
Nikolaev, V. S. 2010 Dynamics of the triple contact line on a nonisothermal heater at partial wetting. Phys. Fluids 22, 082105.Google Scholar
Sohl, C. H., Miyano, K. & Ketterson, J. B. 1978 Novel technique for dynamic surface tension and viscosity measurements at liquid–gas interfaces. Rev. Sci. lnstrum. 49, 1464–1469.Google Scholar
Vargaftik, N. B., Vinogradov, Y. K. & Yargin, V. S. 1996 Handbook of Physical Properties of Liquids and Gases Pure Substances and Mixtures, Third Augmented and revised edition. Begell House.Google Scholar