Article contents
Lift on a steady 2-D symmetric airfoil in viscous uniform shear flow
Published online by Cambridge University Press: 28 December 2017
Abstract
We present an investigation into the influence of upstream shear on the viscous flow around a steady two-dimensional (2-D) symmetric airfoil at zero angle of attack, and the corresponding loads. In this computational study, we consider the NACA 0012 airfoil at a chord Reynolds number 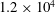 $1.2\times 10^{4}$ in an approach flow with uniform positive shear with non-dimensional shear rate varying in the range 0.0–1.0. Results show that the lift force is negative, in the opposite direction to the prediction from Tsien’s inviscid theory for lift generation in the presence of positive shear. A hypothesis is presented to explain the observed sign of the lift force on the basis of the asymmetry in boundary layer development on the upper and lower surfaces of the airfoil, which creates an effective airfoil shape with negative camber. The resulting scaling of the viscous effect with shear rate and Reynolds number is provided. The location of the leading edge stagnation point moves increasingly farther back along the airfoil’s upper surface with increased shear rate, a behaviour consistent with a negatively cambered airfoil. Furthermore, the symmetry in the location of the boundary layer separation point on the airfoil’s upper and lower surfaces in uniform flow is broken under the imposed shear, and the wake vortical structures exhibit more asymmetry with increasing shear rate.
$1.2\times 10^{4}$ in an approach flow with uniform positive shear with non-dimensional shear rate varying in the range 0.0–1.0. Results show that the lift force is negative, in the opposite direction to the prediction from Tsien’s inviscid theory for lift generation in the presence of positive shear. A hypothesis is presented to explain the observed sign of the lift force on the basis of the asymmetry in boundary layer development on the upper and lower surfaces of the airfoil, which creates an effective airfoil shape with negative camber. The resulting scaling of the viscous effect with shear rate and Reynolds number is provided. The location of the leading edge stagnation point moves increasingly farther back along the airfoil’s upper surface with increased shear rate, a behaviour consistent with a negatively cambered airfoil. Furthermore, the symmetry in the location of the boundary layer separation point on the airfoil’s upper and lower surfaces in uniform flow is broken under the imposed shear, and the wake vortical structures exhibit more asymmetry with increasing shear rate.
JFM classification
- Type
- JFM Rapids
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 12
- Cited by


