Article contents
Levitation of non-magnetizable droplet inside ferrofluid
Published online by Cambridge University Press: 22 October 2018
Abstract
The central theme of this work is that a stable levitation of a denser non-magnetizable liquid droplet, against gravity, inside a relatively lighter ferrofluid – a system barely considered in ferrohydrodynamics – is possible, and exhibits unique interfacial features; the stability of the levitation trajectory, however, is subject to an appropriate magnetic field modulation. We explore the shapes and the temporal dynamics of a plane non-magnetizable droplet levitating inside a ferrofluid against gravity due to a spatially complex, but systematically generated, magnetic field in two dimensions. The coupled set of Maxwell’s magnetostatic equations and the flow dynamic equations is integrated computationally, utilizing a conservative finite-volume-based second-order pressure projection algorithm combined with the front-tracking algorithm for the advection of the interface of the droplet. The dynamics of the droplet is studied under both the constant ferrofluid magnetic permeability assumption as well as for more realistic field-dependent permeability described by Langevin’s nonlinear magnetization model. Due to the non-homogeneous nature of the magnetic field, unique shapes of the droplet during its levitation, and at its steady state, are realized. The complete spatio-temporal response of the droplet is a function of the Laplace number 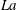 $La$, the magnetic Laplace number
$La$, the magnetic Laplace number 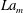 $La_{m}$ and the Galilei number
$La_{m}$ and the Galilei number 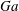 $Ga$; through detailed simulations we separate out the individual roles played by these non-dimensional parameters. The effect of the viscosity ratio, the stability of the levitation path and the possibility of existence of multiple stable equilibrium states is investigated. We find, for certain conditions on the viscosity ratio, that there can be developments of cusps and singularities at the droplet surface; we also observe this phenomenon experimentally and compare with the simulations. Our simulations closely replicate the singular projection on the surface of the levitating droplet. Finally, we present a dynamical model for the vertical trajectory of the droplet. This model reveals a condition for the onset of levitation and the relation for the equilibrium levitation height. The linearization of the model around the steady state captures that the nature of the equilibrium point goes under a transition from being a spiral to a node depending upon the control parameters, which essentially means that the temporal route to the equilibrium can be either monotonic or undulating. The analytical model for the droplet trajectory is in close agreement with the detailed simulations.
$Ga$; through detailed simulations we separate out the individual roles played by these non-dimensional parameters. The effect of the viscosity ratio, the stability of the levitation path and the possibility of existence of multiple stable equilibrium states is investigated. We find, for certain conditions on the viscosity ratio, that there can be developments of cusps and singularities at the droplet surface; we also observe this phenomenon experimentally and compare with the simulations. Our simulations closely replicate the singular projection on the surface of the levitating droplet. Finally, we present a dynamical model for the vertical trajectory of the droplet. This model reveals a condition for the onset of levitation and the relation for the equilibrium levitation height. The linearization of the model around the steady state captures that the nature of the equilibrium point goes under a transition from being a spiral to a node depending upon the control parameters, which essentially means that the temporal route to the equilibrium can be either monotonic or undulating. The analytical model for the droplet trajectory is in close agreement with the detailed simulations.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 9
- Cited by





